Analysis of Algorithm

Due to the large amount of data computers have to deal these days, efficiency would be the most important factor for a good algorithm and data structure

An efficient algorithm : Algorithm that has a short runtime while using the smallest amount of memory resources in the computer

Initially, algorithm was analyzed by measuring the time required for the computer to output its result. However this method requires the algorithm to be implemented and the timing highly depends on the software and hardware environment.

Therefore to solve the problem, a concept called Algorithm complexity analysis was proposed

Algorithm complexity analysis has 2 factors to consider :

• Time complexity : Related to run-time
• Space complexity : Related to storage use

However mostly time complexity is focused. Normally, the number of operations (ex: addition, insertion etc.) are used to represent time complexity.

In a program, the number of operations aren't a constant however is dependent on the number of inputs : n
-> Therefore time complexity can be represented as a function of n : T(n)

Ex) All 3 algorithms are calculating n*n in a different way

for i<-1 to n do
    sum <- sum + n;

for i<-1 to n do
    for j<-1 to n do
       sum <- sum + 1;

Calculate total ops for each algorithm (exluce the operations conducted in the for loop control)
Algorithm A : Product ops 1, Insertion ops 1 -> Total ops = 2
Algorithm B : Addition ops n, Insertion ops n -> Total ops = 2n
Algorithm C : Addition ops n*n, Insertion ops n*n -> Total ops = 2n^2

If we assume all operations require t amount of time the total time required for the algorithms would be 2, 2nt, 2n^2t respectively

The difference between algorithms get larger as n becomes larger

Big Oh(O) Notation

Normally the relationship between input number n and time complexity function T(n) may become very complicated, which is why the Big-Oh notation was introduced

Big-oh notation removes unimportant info in the Time complexity function to give an easier insight of algorithm analysis

Normally in a T(n) with multiple terms, it only takes the term that consists of the highes degree(power)

Ex) T(n) = n2+n+1 -> O(n2)

Note : log n is not ignored as log n also consists of a degree

Big-Oh notation definition :
f(n) = O(g(n)) means there are positive constants c and k, such that 0 ≤ f(n) ≤ cg(n) for all n ≥ k.
(The values of c and k must be fixed for the function f and must not depend on n)

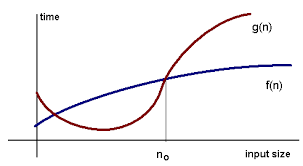
The following picture shows that after n>no, g(n)>f(n) : g(n) is f(n)'s max limit
(Normally, we do not specify c and no as there can be multiple values that satisfy the condition

By using Big-Oh notation (which shows the approximate run-time based on operations depended by number of inputs)

Basic comparison of algorithms based on runtime :
O(1) < O(log n) < O(n) < O(n logn) < O(n2) < O(n!)

Note : When the constant or Coefficient has a very large value, it affects the overall runtime therefore can't be ignored

Other notations

The limit of Big-Oh notation is that it only shows the max limit (which a function can have multiple max limits : f(n)=O(n) but also can be f(n)=O(n2)

To improve the problem, other notations where introduced

Big-Omega (Ω) and Big-Theta (Θ)

Big-Omega notation is to represent the lower limit of the function

Big-Omega definition :
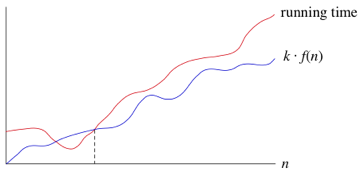
If a running time is Ω(f(n)), then for large enough n, the running time is at least k · f(n) for some constant k.

Big-Theta notation is used when a function can be used to represent both the max and moin limit : Where a function can satisfy both f(n) = O(g(n)) and f(n) = Ω(g(n))
--> We call this situation f(n) = Θ(g(n))

Best, Worst, Average Case

A same algorithm can show different running time based on the set of inputs. The efficiency of an algorithm can be divided in to 3 cases based on the input set

• Worst case : Takes the longest run time
• Best case : Takes the shortest run time
• Average case : Considers all of the input and the probability of each input case to occur to calculate the run time

It shows that the average case would be the most accurate one to asses an algorithm. However considering all of the inputs require too much time. Therefore normally the worst case is used to analyze an algorithm

Ex) Asses a search algorithm which uses an array anc compares each value in the array until it finds the target value

Best case : The target value is stored in the first element of array
Worst case : The target value is stored in the last element of array
Average case : Each element has a probability of 1/n to be searched. The total number of operations where each element consists of the target value would be (1+2+...+n)
Therefore the average case would be (1+2+...+n)/n = (n+1)/2