1. Minimum Spanning Tree
Spanning tree
A Spanning tree is a tree that includes every vertex in the graph. A spanning tree is a special form of a tree that
- has every vertices connected
- does not contain a cycle
Every spanning tree connects n vertices with (n-1) number of edges
A spanning tree can be made by using the edges during DFS and BFS. For example :
depth_first_search(v) :
Mark v as visited;
for (all u ∈ (vertices connected to v) ) do
if(u is not visited yet)
then show thant edge (v,u) is a part of the spanning tree
depth_first_search(u);Spanning tree application : Used in construction of communication network (normally when the least number of edges are required)
Minimum spanning Tree
MST is a tree that considers the weight of each edge. It is a spanning tree that uses the edges that have the smalles total weight
Normally Kruskal's MST algorithm and Prim's algorithm is most famous to get the MST. Conditions for MST :
- The total weight of edge must be minimum
- Should use (n-1) edges
- Must not include a cycle in the tree
Kruskal's MST algorithm
Kruskal's algorithm mainly uses the greedy method (one of the algorithm construction techniques) : Selecting the best option in current status to reach the final answer
However it is never confirmed that, selecting the best option in that situation leads to optimum solution. Therefore you have to assess if the answer is actually the optimum solution for greedy method. For Kruskal, it has been proved that it always gives the optimum solution.
Algorithm :
1. Sort all the edges in non-decreasing order of their weight.
2. Pick the smallest edge. Check if it forms a cycle with the spanning tree formed so far. If cycle is not formed, include this edge. Else, discard it.
3. Repeat step#2 until there are (V-1) edges in the spanning tree.
Pseudo code :
//E : set of edges, G : graph structure
//Et : Set of edges in the MST
kruskal(G) :
E is ordered in decreasing order such that w(e1)<=...w(e2)
Et = NULL, int ecounter = 0;
int k=0;
while(ecounter < (n-1))
k = k+1;
if Et U {e(k)} does not form a cycle
then include the e(k) to Et set
return EtAn important part of the algorithm is to check whether the edge considered will form a cycle with the edges in the set. Therefore Unifon Find algorithm is used inside the Kruskal's algorithm
Union-Find Algorithm
Main concept
Cycle formed : The 2 vertices of the connecting edge both come from the same set of vertices
Cycle X formed : The 2 vertices of the connecting edge come from different set of vertices
We use two additional helping functions for the algorithm : union(x,y) and find(x)
union(x,y) : Input the 2 sets that element x and y are associated in, and combine the 2 sets into 1 set
find(x) : Return the set that element x is a memeber of
Implementation of algorithm
To track the sets of each element, 1D array is used. In 1D array, the index of each element's parent node is stored. If elements have equal parent node ID, it means that the elements are in same set
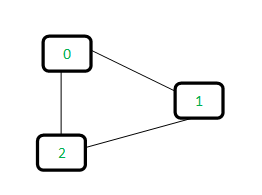
For the following example,
1) When initially there is no link all value of array is initialized to -1 (->means that there is only 1 item in every subset)
0 1 2
-1 -1 -12) Then edge 0-1 is formed : Find the subset in which vertices 0 and 1 are. Since they are in different subsets, we unify them.
For the union, we can take either 0 or 1 as the parent node and it does not matter (in this case assume 0 is parent node)
0 1 2
-1 0 -1The index of the parent node(0) is stored in the element 1 position. Since 0 is the parent node, its value in array is -1
Code :
//Array to store the parent index of each vertex
int parent[MAX_VERTICES];
//Function that returns the representative node (root node) of the set that curr is a member of
int set_find(int curr) {
if(parent[curr] == -1) //The following node is the root node
return curr;
//If current node is not parent, moves to the parent node of the current node
//Repeat moving up to the parent node till it reaches the root node
while(parrent[curr] != -1) curr = parent[curr];
return curr;
}
//Combine the to sets together
void set_union(int a, int b) {
int root1 = set_find(a); //Find root node of a
int root2 = set_find(b); //Find root node of b
//The set where root 1 was the root node now has root 2 as the root node
//The root 1 now points root 2 to be its parent node
if(root1!=root2)
parent[root1] = root2;
}Implementation of Kruskal's algorithm
In Kruskal's algorithm we would have to sort the edges and therefore Graph is represented as a set of edges only. (GraphType only storees edges)
//Structure to represent a weighted edge in graph
struct Edge {
int start, end, weight;
};
//Structure to represent the graph
struct GraphType {
int n; //Number of edges
struct Edge *edge; //The graph is represented as an array of edges
}
//Creates the graph with number of edges initialized
//Use dynamic memory allocation to efficiently use memory
struct GraphType* createGraph(int E)
{
struct GraphType* graph = (struct GraphType*)(malloc(sizeof(struct Graph)));
graph->n = E;
//Create an array with size of the number of edges input
graph->edge = (struct Edge*)malloc(sizeof(struct Edge)*E);
return graph;
}
// Compare two edges according to their weights.
// Used in qsort() for sorting an array of edges
int myComp(const void* a, const void* b)
{
struct Edge* a1 = (struct Edge*)a;
struct Edge* b1 = (struct Edge*)b;
return a1->weight > b1->weight;
}
//Main function to construct MST using Kruskal's algorithm
//Assume the graph is all set with all of the nodes connected to each other
void KrsukalMST(struct GraphType *g) {
int edge_accepted = 0; //Number of edges inside the MST
int uset, vset; //Root node for set u and v
struct Edge e;
int i=0; //Index variable used for sorted edges
//Step 1 : Sort all the edges in non-decreasing order of their weight
qsort(g->edges, g->n, sizeof(struct Edge), compare);
while(edge_accepted < (g->n - 1)) { //Repeat till num of edges < (n-1)
//Step 2 : Pick the smallest edge and increment the index for next iteration
e = g->edges[i++];
//Find the set(root node) that each vertex of edge is associated to
//The root node index is stored in each variable
uset = set_find(e.start);
vset = set_find(e.end);
//If they both are from different set, unify the two into 1 uniton
if(uset != vset) {
printf("Edge (%d, %d) selected", e.start, e.end);
edge_accepted++;
//Unify the two sets together
set_union(uset,vset);
}
}
}Time complexity for the following algorithm depends on the time to sort the edges :O(ElogE)
Prim's MST algorithm
Prim's algorithm basically starts from a node and expands the set of nodes consecutively. At the start, only 1 node is included in the set.
Prim's algorithm selects the closest node that is directly linked to the nodes in the set, and adds it to the set. This process is repeated till the tree has (n-1) edges.
Comparison with Kruskal's algorithm :
- Kruskal's -> based on edges, Prim's -> based on vertices
- Kruskal's -> Is not effected by the previously made MST, Prim's -> Expanding based on the previously made MST
Basic algorithm for Prim's MST algorithm :
1. Create a set that keeps track of vertices already included in MST
2. Asign a key value to all vertices in the input graph. Initially all key values are set to INFINITE, except for the first vertex (key value:0) so that it is picked first
3. While the set doesn't include all vertices repeat :
- Pick a vertex u in which is not in the set and has minimum key value
- Include u to the set
- Update the key value of all adjacent vertices of u :
(1) To update the key values, iterate through the adjacent vertices
(2) For every adjacent vertex v, if weight of edge (u,v) < previous key value of v update the key value as weight of (u,v)
The key values represent the minimum weight edges connecting them to the set of vertices included in MST
Implementation of Prim's algorithm
- Basically a 2x2 matrix is used to represent the Graph shape : Easy to represent the connection between any two vertices
- An array mstSet[] is used to represent the set of vertices included in MST (if mstSet[v] == true -> v is included in set)
- Array distance[] is used to store key values of all vertices
- parrent[] array is used to show the constructed MST
Code :
int distance[MAX_VERTICES];
int mstSet[MAX_VERTICES];
int parent[MAX_VERTICES];
typedef struct GraphType {
int n;
int weight[MAX_VERTICES][MAX_VERTICES];
} GraphType;
//Return the index of vertex with the smalles dist[v]
int get_min_vertex(int n) {
//Initialize min value
int min = INT_MAX;
int min_index
for (int v=0; v<n; v++) {
//Compare the distance of selected vertex with all the other vertices that are not in the set.
//Find vertex with smallest distance and return position index
if(mstSet[v]==false && key[v] < min) {
min = key[v], min_index = v;
}
}
return min_index;
}
//Function to construct MST graph
void primMST (GraphyType *g) {
//Initialize all the distance to INFINITE
//Initialize set so that there is no vertex included initially
for (int i=0; i<g->n; i++) {
distance[i] = INT_MAX;
mstSet[i] = false;
}
//1st node in initially included in the set
//The vertex with position index of 0 is added
distance[0] = 0;
parent[0]=-1; //First node is always root of MST
for(int i=0; i<g->n; i++) {
//Pick the minimum distance vertex from the set of vertices not in the MST
int y = get_min_vertex(g->n);
//Add the picked vertex to the MST set
mstSet[u] = true;
//Update the distance value and parent index of the adjacent vertices of the vertices not included in MST
for(int v=0; v<g->n; v++) {
//graph[u][v] is non zero only for adjacent vertices of u
//mstSet[v] is false for vertices not included in MST
//distance[v] represents the distance between v and the node that was originally closest to v that is included in MST
//Update distance[v] only if the newly added u node has a closer distance to v
if(g->weight[u][v] && g->weight[u][v] < distance[v]) {
parent[v] = u;
distance[v] = g->weight[u][v];
}
}
}
}Time complexity of Prim's algorithm
The main iterative function in Prim's has a double loop, therefore has a time complexity of O(n2)
Therefore Kruskals algorithm : Appropriate for sparse graph,
Prims algorithm : Appropriate for dense graph
2. Shortest path
The shortest path question is to find the shortest path that connects two vertices i and j. Unlike MST, it focuses on finding the path therefore does not require all vertices to be included in the path. There are 2 algorithms to find the shortest path.
- Dijkstra's shortest path algorithm
- Floyd's algorithm
Dijkstra's shortest path algorithm
Objective : Finds the shortest path's distance from one ceratin vertext to every other vertices.
The algorithm creates the tree of the shortest paths from the starting source vertex from all other points in the graph. We first start with an empty set S={}. Starting from the source node, nodes are added in order based on the distance between node and source node.
Algorithm
- First mark all vertex as unvisited
- Mark the
distanceof source vertex as 0 and all ogher vertices as infinity - Consider source vertex as current vertex
- Calculate the path length of all directly linked vertex from the source vertex by :
(weight of the link in current vertex to the neighbour vertex) + (distance from source vertex to current vertex) - If calculated path length is smaller than pervious path lenght in
distance, then replace it otherwise ignore - Mark current vertex as visited after visiting the nieghvor vertex of current vertex
- Select the next vertex with smallest
distancevalue and go back to step 4 - Repeat till all vertex are visited
Implementation of dijkstra's algorithm
Distance array
- It is required to record the distance between the start node and other nodes, therefore is stored in a 1D array :
distance[] - As nodes get added, we update the
distance[]:
If the (distance of (source node)<->(current node)) + (distance of (current node)<->(neighbor node)) is smaller than the value insidedistance[], it is replaced
distance[w] = min(distance[w], distance[u]+weight[u][w])
(where v : source node, u : newly added node, w : node directly linked to u)
Output of dikstra's algorithm
When the dikstra's algorithm is done the distance[] would store the minimum value of the distance between the source vertex to each vertices. The path is not directly stored therefore an additional array is required to store the path
Path array
We create a sepreate array parent[] to store the parent index to each element. Initially the array is blank, and the source node has a parent[] value of -1 to represent it as the ultimate source node.
but everytime the distance[] value is updated for a certain vertex, the following parent[] value is also upated to point to the new node added to the set to be the parent.
To print the path, we use recursive function till the parent[] value reaches -1.
void printPath(int parent[], int j)
{
// Base Case : If j is source
if (parent[j]==-1)
return;
printPath(parent, parent[j]);
printf("%d ", j);
}Implementation of Dikstra's algorithm
//Return the vertex with minimum distance value within vertices not yet processed(visited)
int minDistance(int distance[], int found[]) {
int min = INT_MAX;
int min_index = -1;
for(int i=0; i<g->n; i++) {
if(distance[i] < min && !found[i]) {
min = distance[i];
min_index = i;
}
}
return min_index;
}
// Function that implements Dijkstra's single source shortest path algorithm
void dijkstra(GraphType *g, int src)
{
// The output array. dist[i]
// Will hold the shortesㅅ distance from src to i
int distance[MAX_VERTICES];
// Represent if vertex was been visited
bool found[MAX_VERTICES];
// Parent array to store parent index
int parent[MAX_VERTICES];
// Initialize all distance and found array values
for (int i = 0; i < V; i++)
{
parent[0] = -1;
distance[i] = INT_MAX;
found[i] = false;
}
// Distance of source vertex from itself is always 0
distance[src] = 0;
// Find shortest path for all vertices
for (int count = 0; count < g->n-1 ; count++)
{
// Pick the minimum distance vertex from the set of vertices not yet processed.
// u is always equal to src in first iteration.
int u = minDistance(distance, found);
// Mark the picked vertex as processed
found[u] = true;
// Update distance value of the adjacent vertices of the picked vertex.
for (int v = 0; v < V; v++)
// Update distance[v] only if is
// not in found and
// There is an edge from u to v, and total weight of path from src to v through u is smaller than current value of dist[v]
if (!found[v] && graph[u][v] && distance[u] + graph[u][v] < distance[v])
{
parent[v] = u;
distance[v] = distance[u] + graph[u][v];
}
}
// print the constructed distance array
printSolution(dist, V, parent);
}Floyd's short path algorithm
Objective : Unlike Dikstra's algorithm, floyd's algorithm finds the shortest path between all of the vertices to each other. A 2x2 array with all of the shortest distance between all vertices are stored.
Algorithm
The algorithm uses 3 nested loops. Initially, the solution matrix is initiailized to the graph itself. The main idea is to pick a certain vertex and update all shortest path between the original one and the one that includes the picked vertex as the intermediate vertex.
Ak[i][j] represents the minimum distance between vertex i to j by using 0~k as the intermediate vertex. The key feature of Floyd's algorithm is to calculate the distance in following order :
A-1, A0, A1, ... , An-1
When calculating the Ak, we consider that we have already considered cases on when the vertex 0~k-1 is an intermeidate vertex and have found the optimal solution.
For every pair (i,j) of the source and destination vertices respectively, there are 2 possible cases
1) When k(the intermediate vertex) is not included in the path from i to j : Min distance remains to be Ak-1[i][j]
2) When k(the intermediate vertex) is included in path from i to j : Distance could be the result of (Ak-1[i][k] + Ak-1[k][j])
(Addition of min distance between i-k and j-k)
=> Therefore conclusively, the min distance would be the smalles one between the result of (1) and (2)
Note : Since if there is no link between i-j and k, it is represented by infinity(very large number), there is no error.
Output of floyds algorithm
Following matrix shows the shortest distances between every pair of vertices
0 5 8 9
INF 0 3 4
INF INF 0 1
INF INF INF 0It shows every shortest distance between any two vertices in the graph.
Implementation of Floyds algorithm
void floyd(GraphType *g) {
//Initialize the answer 2x2 array
for(int i=0; i<g->n; i++) {
for(int j=0; j<g->n; j++) {
A[i][j] = g->weight[i][j];
}
}
//Find the min distance
for(int k=0; k<g->n; k++) {
for(int i=0; i<g->n; i++) {
for(int k=0; k<g->n; k++) {
if(A[i][k] + A[k][j] < A[i][j])
A[i][j] = A[i][k] + A[k][j];
}
}
}
}3. Topology sort
Algorithm to decide the order of tasks that has a specific hierarchy. Some tasks should always come infront of other certain tasks due to relationship.
Ex) The process of university tasks are shown
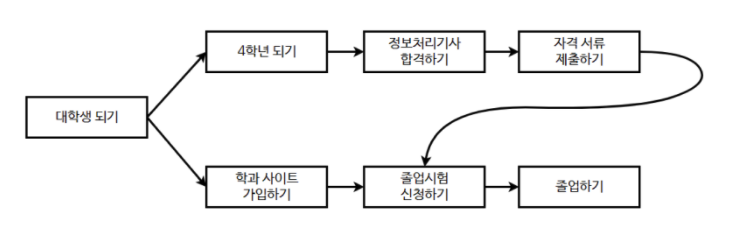
You would not be able to pass the test until you become a senior. However passing the test and signing in the department website is independent and therefore the order does not matter.
A topology sort allgins every task(represented as nodes) in the graph, without violating the precedence order of each task.
For a single graph, there can be several topology sorts as there are tasks that have same hierarchy.
Note that if a graph has a cycle, Topology sort is impossible and would cause an error.
Algorithm
1) Select a node that has no entering edges
2) Delete the following node and all of the links connected to the node
3) Repeate the process till all of the nodes have been deleted
Pseudo code of algorithm
topo_sort(G)
for(i<-0 to n-1)
if(Every node has a preceding node)
then cycle exists and error;
Select a node v that does not have a preceiding node
print v
delete v and every link that is connected to vImplementation of topology sort
- A 1D array
in_degree[]to record the number of edges pointing to the node, for every node - If
in_degree[i] == 0it becomes the next candidate to be deleted - The deleted vertex will cause the directly linked vertices to have the
in_degree[]value decrease by 1 - Use stack to be able to store the candidate vertices in which they do not have any edges pointing towards them (
in_degree==0) - If vertex's
in_degree[]value decreases to 0, it is added to the stack - Graph is represented by using linked list
Code of topology sort
int todo_sort(GraphType *g) {
int i;
StackType s;
GraphNode *node;
//Calculate the number of edges entering the vertex for every vertex
//Dynamically allocate an array to store number of entering edges
int *in_degree = (int*)malloc(g->n * sizeof(int));
for(int i=0; i< g->n; i++) {
in_degree[i] = 0;
}
for(int i=0; i<g->n; i++) {
//In each list, the nodes pointed by the head node of each list exists
GraphNode *node = g->adj_list[i];
while(node!=NULL) {
//Get position index of the pointed vertex and increment count by 1
in_degree[node->vertex]++;
node=node->link;
}
}
//Add the node in which in_degree is 0 to stack
init(&s); //Initialize stack
for(int i=0; i<g->n; i++) {
//Push the candidate vertices into the stack
if(in_degree[i]==0) push(&s, i);
}
//Generate topology sort
while(!is_empty(&s)) {
int w;
//w stores entering node's position index
w = pop(&s);
printf("Vertex %d ->", w);
//Get the head node of the list
//Decrease the number of entering index
while(node != NULL) {
int u = node->vertex;
in_degree[u]--;
if(in_degree[u] == 0) push(&s, u);
node=node->link;
}
}
free(in_degree);
}