문제

BOJ 4883: 삼각 그래프 https://www.acmicpc.net/problem/4883

풀이

조건

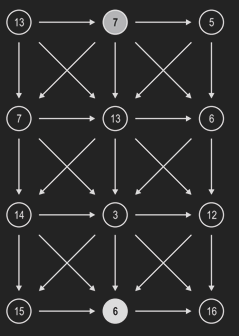
• 삼각 그래프의 가장 위쪽 가운데 정점에서 가장 아래쪽 가운데 정점으로 가는 최단 경로를 찾는 문제이다.
• 밑에서도 올 수 있고 바로 옆에서도 올 수 있다.

풀이 순서

• 1번째 높이는 가운데, 오른쪽 노드의 최단 경로만 구해준다.
• 2번째 높이의 왼쪽은 1번째 높이의 가운데에서만 올 수 있다.
• 2번째 높이의 가운데, 오른쪽은 화살표 대로 모두 올 수 있다.
• 그 이후의 높이는 화살표대로 모두 구현한다.

코드

Java

import java.util.*;
import java.io.*;

public class Main {

	public static void main(String[] args) throws IOException {

		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		StringTokenizer st;
		StringBuilder sb = new StringBuilder();

		int tc = 1;
		while (true) {
			int N = Integer.parseInt(br.readLine());
			
			// 종료 조건
			if (N == 0)
				break;
			
			// 입력 받은 삼각 그래프
			int[][] graph = new int[N + 1][3];

			for (int i = 1; i <= N; i++) {
				st = new StringTokenizer(br.readLine(), " ");
				for (int j = 0; j < 3; j++) {
					graph[i][j] = Integer.parseInt(st.nextToken());
				}
			}
			
			// DP 배열은 1_000_001으로 초기화
			long[][] dp = new long[N + 1][3];
			for (int i = 0; i <= N; i++) {
				for (int j = 0; j < 3; j++) {
					dp[i][j] = 1_000_001;
				}
			}
			
			// DP 배열의 각 위치별 최소값 구하기
			dp[1][1] = graph[1][1]; // 1번째 높이의 가운데

			dp[1][2] = dp[1][1] + graph[1][2]; // 1번째 높이의 오른쪽

			dp[2][0] = dp[1][1] + graph[2][0]; // 2번째 높이의 왼쪽
			
            // 2번째 높이의 가운데
			dp[2][1] = Math.min(dp[2][1], 
					Math.min(dp[1][1] + graph[2][1], 
					Math.min(dp[1][2] + graph[2][1], 
							dp[2][0] + graph[2][1])));
			
            // 2번째 높이의 오른쪽
			dp[2][2] = Math.min(dp[2][2],
					Math.min(dp[1][1] + graph[2][2], 
					Math.min(dp[2][1] + graph[2][2], 
							dp[1][2] + graph[2][2])));
			
            // DP 배열 값 찾기
			for (int i = 3; i <= N; i++) {
            	// 왼쪽 노드까지 오는 데 드는 비용의 최소값 찾기
				dp[i][0] = Math.min(dp[i][0],  // 현재 노드
						Math.min(dp[i - 1][0] + graph[i][0], // 이전의 왼쪽에서 온 경우
								dp[i - 1][1] + graph[i][0])); // 이전의 가운데에서 온 경우
				
                // 가운데 노드까지 오는 데 드는 비용의 최소값 찾기
				dp[i][1] = Math.min(dp[i][1], // 현재 노드
						Math.min(dp[i - 1][0] + graph[i][1], // 이전의 왼쪽에서 온 경우
						Math.min(dp[i - 1][1] + graph[i][1], // 이전의 가운데에서 온 경우
						Math.min(dp[i][0] + graph[i][1], // 현재 노드의 바로 왼쪽에서 온 경우
								dp[i - 1][2] + graph[i][1])))); // 이전의 오른쪽에서 온 경우
				
                // 오른쪽 노드까지 오는 데 드는 비용의 최소값 찾기
				dp[i][2] = Math.min(dp[i][2], // 현재 노드
						Math.min(dp[i - 1][1] + graph[i][2], // 이전의 가운데에서 온 경우
						Math.min(dp[i][1] + graph[i][2], // 현재 노드의 바로 왼쪽에서 온 경우
								dp[i - 1][2] + graph[i][2]))); // 이전의 오른쪽에서 온 경우
			}

			sb.append(tc).append(". ").append(dp[N][1]).append("\n");

			tc++;
		}

		System.out.println(sb);
	}
}

정리

• 바로 옆에서도 올 수 있는데 그 부분을 체크하지 못해서 틀렸었다.