오늘은 이진탐색 알고리즘에 대해서 공부해겠습니다. 🙆♀️
✨ 선형 탐색(linear search)
탐색을 하려는 요소들이 정렬되어 있지 않은 경우에 가장 간단하고 직접적인 탐색 방법으로 "선형 탐색"을 할 수 있다.
탐색이 한쪽 끝에서 다른 한 쪽 끝으로 나아가는 방식이라고 할 수 있다.
탐색을 시작해서, 결과를 찾을 때까지 루프를 반복하고 결과를 찾으면 탐색을 종료하는 식으로 구현한다.
function solution(array, key) {
for (let i = 0; i < array.length; i++) {
if (array[i] === key) {
return i;
}
}
}
console.log(solution([2, 4, 5, 1, 6], 2)); // 최선의 경우: 한번의 탐색으로 해결
console.log(solution([2, 4, 5, 1, 6], 6));// 최악의 경우: 배열의 크기만큼 탐색선형 탐색은 찾는 대상이 앞쪽에 있으면, 짧은 시간 안에 탐색할 수 있지만 탐색 대상이 뒤 쪽에 있거나 혹은 아예 존재하지 않을 경우 그리고 데이터의 양이 많아질 수록 시간이 많이 걸려 비효율적이라고 할 수 있다.
배열의 크기에 따라 시간이 비례적으로 증가하므로 시간 복잡도는 O(n)이라고 할 수 있다.
✨ 이진탐색(binary search)
배열의 중앙에 있는 값을 조사하여 찾고자 하는 항목이 왼쪽 또는 오른쪽 부분의 배열에 있는지를 알아내어 탐색의 범위를 반으로 줄여나가는 과정
이때 주의할 점은 원소들이 오름차순이나 내림차순으로 정렬되어 있는 경우에만 사용할 수 있는 탐색 알고리즘이라는 것!
◻ 이진탐색의 시간복잡도
중간 값과 찾고자하는 값의 비교가 이루어질때마다 탐색의 범위가 1/2로 줄어든다.
O(log(n))
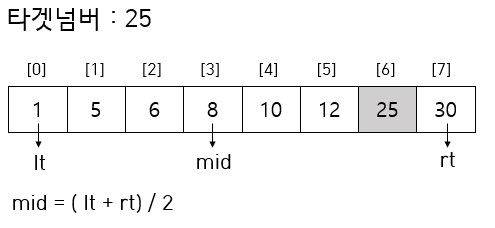
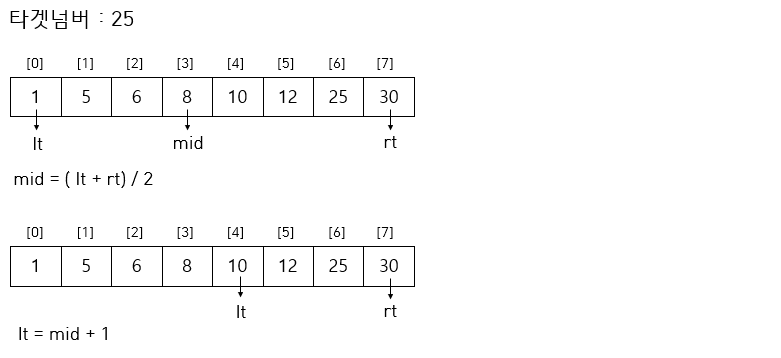
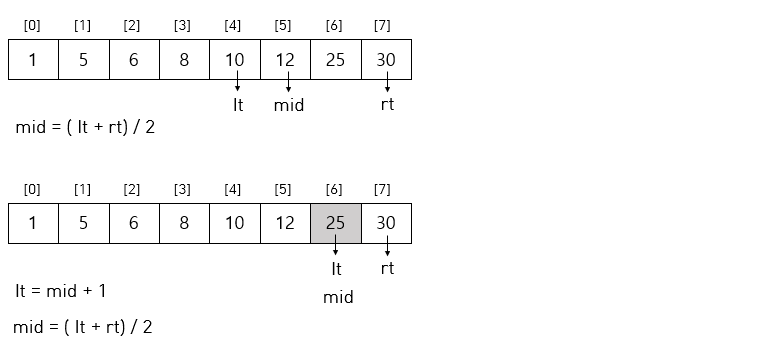
◻ 이진탐색 과정
- 찾고자하는 값과 범위의 중앙값과 비교
- 찾으려는 값이 중앙값보다 작으면 범위를 왼쪽 절반으로 한정시켜 다시 중앙값과 비교
- 찾으려는 값이 중앙값보다 크면 범위를 오른쪽 절반으로 한정시켜 다시 중앙값과 비교
- 값을 찾을 때까지 반복하여, 목표값을 찾으면 탐색 종료
◻ 이진탐색 구현
이진탐색은 크게 재귀(recursion)과 반복(iteration) 2가지 방법으로 구현할 수 있다. 일반적으로는 반복(iteration) 방식으로 구현하는 것이 성능이 좋은 편이고, 간편하다.
우선 c++ 코드로 보면
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
int main() {
int n, key, temp, lt = 0, rt, mid;
cin >> n >> key;
vector<int> arr;
for (int i = 0; i < n; i++) {
cin >> temp;
arr.push_back(temp);
}
sort(arr.begin(), arr.end()); //먼저 정렬
rt = n - 1; //배열의 끝 값
while (lt <= rt) {
mid = (lt + rt) / 2;
if (arr[mid] == key) {
cout << mid;
break;
}
else if (arr[mid] < key) lt = mid + 1; // 오른쪽 절반
else rt = mid - 1; // 왼쪽 절반
}
return 0;
}◻ 자바스크립트로 구현
function binarySearch(array, target) {
let lt = 0;
let rt = array.length - 1;
while (lt <= rt) {
let mid = Math.floor((lt + rt) / 2); // 몫
if (array[mid] === target) {
return mid;
} else if (array[mid] > target) {
rt = mid - 1;
} else {
lt = mid + 1;
}
}
return -1;
}
console.log(binarySearch([1, 5, 6, 8, 10, 12, 25, 30], 25)); // 6◻ 활용 문제
백준 2110 : 공유기 설치
◽ 문제설명
도현이의 집 N개가 수직선 위에 있다. 각각의 집의 좌표는 x1, ..., xN이고, 집 여러개가 같은 좌표를 가지는 일은 없다.
도현이는 언제 어디서나 와이파이를 즐기기 위해서 집에 공유기 C개를 설치하려고 한다.
최대한 많은 곳에서 와이파이를 사용하려고 하기 때문에, 한 집에는 공유기를 하나만 설치할 수 있고, 가장 인접한 두 공유기 사이의 거리를 가능한 크게 하여 설치하려고 한다.
C개의 공유기를 N개의 집에 적당히 설치해서, 가장 인접한 두 공유기 사이의 거리를 최대로 하는 프로그램을 작성하시오.◽ 정리: 가장 인접한 두 점 사이의 거리가 최대가 되도록 C개의 공유기를 설치해라!
◽ 접근
- 우선 입력받은 수를 정렬
- 두 점 사이의 거리는 가장 작은 수 ~ 가장 큰 수 사이일 것
- '가장 가까운 말의 최대 거리'를 정한 후, 나머지 말들 사이의 거리는 이 거리보다 크도록 설치
- 설치한 말들의 개수에 따라 이분 탐색 수행
◽ 코드
function count(arr, c) {
let cnt = 1,
ep = arr[0]; //ep: 바로 직전에 설치한 좌표
for (let i = 1; i < arr.length; i++) {
if (arr[i] - ep >= c) {
// 공유기 설치
cnt++;
ep = arr[i];
}
}
return cnt;
}
function solution(arr, c) {
let answer;
arr.sort((a, b) => a - b); //오름차순 정렬
let lt = 1; // 최소거리
let rt = arr[arr.length - 1]; //최대거리
while (lt <= rt) {
let mid = parseInt((lt + rt) / 2);
if (count(arr, mid) >= c) {
answer = mid;
lt = mid + 1;
} else {
rt = mid - 1;
}
}
return answer;
}
console.log(solution([1, 2, 8, 4, 9], 3)); // 3