MST & Dijkstra Algorithm

Y·2021년 12월 16일

JavaScript algorithm dijkstra

신장트리 (Spanning Tree)

그래프 내의 모든 정점을 포함하는 트리

최소 연결 = 간선의 수가 가장 적다
n개의 정점을 가지는 그래프의 최소 간선 수는 (n-1)개이고, 모든 정점이 (n-1)개의 간선으로 이루어진 트리를 신장트리라고 한다
사이클을 포함해서는 안된다
하나의 그래프에는 많은 신장 트리가 존재할 수 있다

MST(Minimum Spanning Tree)

최소 신장 트리

(정점-1) 개의 간선으로 이루어진 신장트리 중에서 가중치의 합이 가장 작은 것
선택된 간선은 사이클을 만들지 않아야하고, 가중치가 작은 것들부터 골라져야 한다

MST의 특징

간선의 가중치 합이 최소
n개의 정점을 가지는 그래프에 대해 반드시 (n-1)개의 간선만을 사용해야한다
사이클이 포함되어서는 안된다

MST의 구현 방법

Kruskal MST 알고리즘

: 이전 단계에서 만들어진 신장 트리와는 상관없이 무조건 최소 간선만을 선택하는 방법
"간선" 선택을 중심으로 하는 알고리즘

과정
(1) 그래프의 간선들을 가중치의 오름차순으로 정렬
(2) 정렬된 간선 리스트에서 순서대로 사이클을 형성하지 않는 간선을 선택

가장 낮은 가중치를 먼저 선택
사이클을 형성하는 간선 제외

(3) 해당 간선을 현재의 MST의 집합에 추가

예시

먼저 간선들의 가중치를 중심으로 오름차순 정렬한다

간선 (a, f) 선택
간선 (c, d) 선택
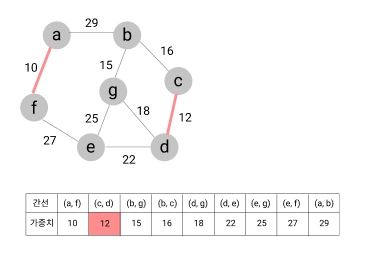
간선 (b, g) 선택
간선 (b, c) 선택
간선 (d, g) 선택 => 사이클 형성되므로 제외
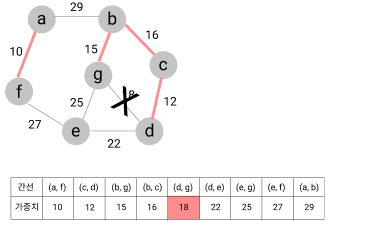
간선 (d, e) 선택
간선 (e, g) 선택 => 사이클 형성되므로 제외
간선 (e, f) 선택 => (n-1)개의 간선 생성되었으므로 종료

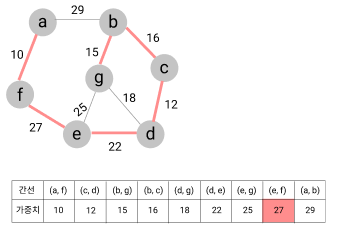
주의점
다음 간선을 선택할 때, 사이클을 생성하는지 확인
=> 사이클 생성 여부 확인하는 방법: 추가하고자 하는 간선의 양끝 정점이 같은 집합에 속해 있는지 먼저 검사
=> union-find 알고리즘

Javascript Code

class unionfind {
  constructor(elements) {
    this.parent = {};
    elements.forEach((e) => (this.parent[e] = e)); // 자기 자신을 부모 노드로 초기화
  }

  union(a, b) {
    let roota = this.findparent(a);
    let rootb = this.findparent(b);

    if (roota === rootb) {
      console.log("이미 연결되어 있다");
      return false;
    }

    // 작은 부모 노드 값을 가진 쪽으로 합친다 (f의 부모노드를 a로..)
    if (roota > rootb) {
      if (this.parent[b] != b) this.union(this.parent[b], a);
      this.parent[a] = this.parent[b];
      return true;
    } else {
      if (this.parent[a] != a) this.union(this.parent[a], b);
      this.parent[b] = this.parent[a];
      return true;
    }
  }

  findparent(a) {
    while (this.parent[a] !== a) {
      a = this.parent[a];
    }
    return a;
  }
}

class Kruskal {
  constructor(nodes, edges) {
    this.nodes = new unionfind(nodes);
    this.edges = edges; // 간선 리스트
    this.graph = []; // 최소 신장 트리 담는 곳
  }

  mst() {
    while (this.edges.length > 0) {
      this.findmin();
    }
    console.log(this.graph);
  }

  findmin() {
    //간선 선택해나가는 과정
    this.edges.sort(function (first_node, second_node) { // 가중치를 중심으로 오름차순 정렬
      return first_node[2] - second_node[2];
    });
    let minweight = this.edges.shift(); // 가장 작은 가중치를 가진 간선 선택
    let result = this.nodes.union(minweight[0], minweight[1]); // 연결하기 (false: 이미 연결되어있다)
    if (result) {
      this.graph.push(minweight);
    }
  }
}

let nodes = ["a", "b", "c", "d", "e", "f", "g"];
let edges = [
  ["a", "b", 29],
  ["a", "f", 10],
  ["e", "f", 27],
  ["d", "e", 22],
  ["b", "g", 15],
  ["e", "g", 25],
  ["b", "c", 16],
  ["c", "d", 12],
  ["d", "g", 18]
];

let kruskal = new Kruskal(nodes, edges);
kruskal.mst();

/*
[
  [ 'a', 'f', 10 ],
  [ 'c', 'd', 12 ],
  [ 'b', 'g', 15 ],
  [ 'b', 'c', 16 ],
  [ 'd', 'e', 22 ],
  [ 'e', 'f', 27 ]
]
*/

Prim MST 알고리즘

: 시작 정점에서부터 출발하여 신장트리 집합을 단계적으로 확장해나가는 방법
"정점" 선택을 중심으로 하는 알고리즘
=> 이전 단계에서 만들어진 신장트리를 확장하는 방식

과정
(1) 시작 단계에서 시작 정점만이 우선 MST 집합에 포함된다
(2) 앞 단계에서 만들어진 MST 집합에 인접한 정점들 중에서 최소 간선으로 연결된 정점을 선택하여 트리를 확장한다
=> 즉, 가장 낮은 가중치를 먼저 선택한다

(3) 트리가 (n-1)개의 간선을 가질 때까지 위의 과정을 반복한다

예시

시작 정점 포함
인접 정점 중 최소 간선으로 연결된 정점 선택 => f 정점

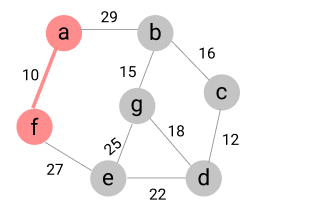
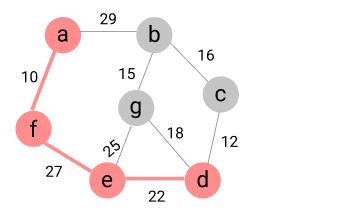
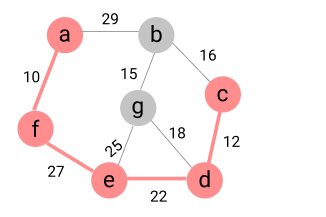
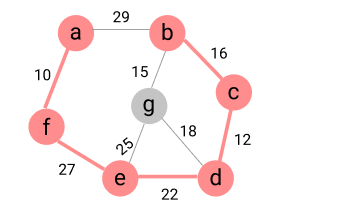
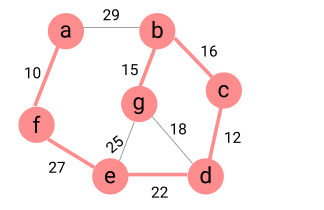
=> (n-1) 개의 간선 선택 완료 했으므로 종료한다

Dijkstra Algorithm

: 최단 경로를 찾는(Shortest Path) 탐색 알고리즘
"정점" 선택을 중심으로 하는 알고리즘

음의 간선이 존재하지 않기 때문에 다익스트라는 현실 세계에 사용하기 매우 적합한 알고리즘
Dynamic Programming 문제 => 최단 거리는 여러 개의 최단 거리로 이루어져 있기 때문
=> 하나의 최단 거리를 구할 때 그 이전까지 구했던 최단 거리 정보를 그대로 사용

출발 정점으로부터 다른 모든 정점까지의 거리를, (1) 선택된 정점을 지나서 가는 경우와 (2) 직접 가는 경우 중 최솟값으로 갱신해가면서

가장 가까운 정점을 하나씩 선택된 정점에 편입시켜가며 최단경로를 갱신

과정
(1) 출발 노드를 설정
(2) 출발 노드를 기준으로 각 노드의 최소 비용을 저장
(3) 방문하지 않은 노드 중에서 가장 비용이 적은 노드를 선택
(4) 해당 노드를 거쳐서 특정 노드로 가는 경우를 고려하여 최소 비용을 갱신
(5) 위의 (3)~(4) 과정을 반복

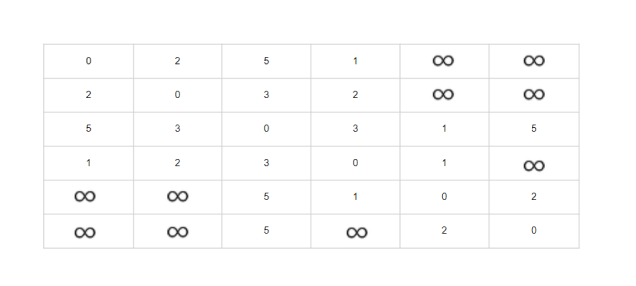
정점 v에서 정점 w로의 직접 간선이 없는 경우 무한대의 값을 저장

집합 S에 최단 거리에 해당하는 정점이 하나씩 추가됨

최단 거리를 기록하는 1차원 배열 distance
distance[w] = min(distance[w], distance[u] + weight[u])

예시

1번 노드 선택

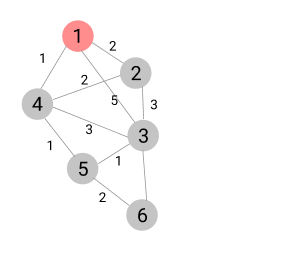
S = { 1 }
1번 노드에서 다른 정점으로 가는 최소 비용

방문하지 않은 노드 중에서 가장 비용이 적은 노드는 4번 노드

4번 노드 선택

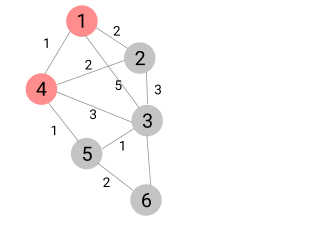
S = { 1, 4 }
4번 노드를 거쳐서 가는 경우를 모두 고려하여 최소 비용 배열 갱신

1번 -> 3번 : 4로 갱신 (1번 -> 4번 -> 3번)
1번 -> 5번 : 2로 갱신 (1번 -> 4번 -> 5번)

방문하지 않은 노드 중에서 가장 비용이 적은 노드는 2번 노드

2번 노드 선택

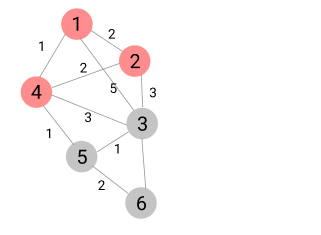
S = { 1, 4, 2 }
2번 노드를 거쳐서 가는 경우를 모두 고려하여 최소 비용 배열 갱신

방문하지 않은 노드 중에서 가장 비용이 적은 노드는 5번 노드

5번 노드 선택

S = { 1, 4, 2, 5 }
5번 노드를 거쳐서 가는 경우를 모두 고려하여 최소 비용 배열 갱신

1번 -> 3번 : 3으로 갱신 (1번 -> 5번 -> 3번)
1번 -> 6번 : 4로 갱신 (1번 -> 5번 -> 6번)

방문하지 않은 노드 중에서 가장 비용이 적은 노드는 3번 노드

3번 노드 선택

S = { 1, 4, 2, 5, 3 }
2번 노드를 거쳐서 가는 경우를 모두 고려하여 최소 비용 배열 갱신

마지막으로 남은 6번 노드

6번 노드 선택

결론적으로, 1번 노드에서 각 노드로 가는 최소비용은 위의 결과와 같다.

Dijkstra 활용 문제

Programmers 배달

문제
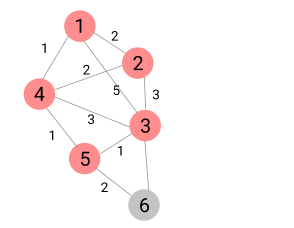
N개의 마을로 이루어진 나라가 있습니다. 이 나라의 각 마을에는 1부터 N까지의 번호가 각각 하나씩 부여되어 있습니다. 각 마을은 양방향으로 통행할 수 있는 도로로 연결되어 있는데, 서로 다른 마을 간에 이동할 때는 이 도로를 지나야 합니다. 도로를 지날 때 걸리는 시간은 도로별로 다릅니다. 현재 1번 마을에 있는 음식점에서 각 마을로 음식 배달을 하려고 합니다. 각 마을로부터 음식 주문을 받으려고 하는데, N개의 마을 중에서 K 시간 이하로 배달이 가능한 마을에서만 주문을 받으려고 합니다. 다음은 N = 5, K = 3인 경우의 예시입니다.

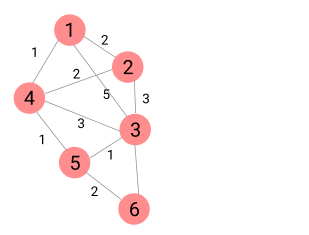
위 그림에서 1번 마을에 있는 음식점은 [1, 2, 4, 5] 번 마을까지는 3 이하의 시간에 배달할 수 있습니다. 그러나 3번 마을까지는 3시간 이내로 배달할 수 있는 경로가 없으므로 3번 마을에서는 주문을 받지 않습니다. 따라서 1번 마을에 있는 음식점이 배달 주문을 받을 수 있는 마을은 4개가 됩니다.
마을의 개수 N, 각 마을을 연결하는 도로의 정보 road, 음식 배달이 가능한 시간 K가 매개변수로 주어질 때, 음식 주문을 받을 수 있는 마을의 개수를 return 하도록 solution 함수를 완성해주세요.

code

distance 배열: INF(무제한)으로 초기화
arr 배열 : 연결된 간선들을 표현하는 배열

  const distance = Array(N + 1).fill(Infinity);
  const arr = Array.from({ length: N + 1 }, () => []); // [ [], [] .. ] 크기: N+1 인 배열

  road.forEach(([a, b, c]) => { // 인접한 노드와 가중치의 정보를 추가
    arr[a].push({ node: b, weight: c });
    arr[b].push({ node: a, weight: c });
  });

[
  [],
  [ { node: 2, weight: 1 }, { node: 4, weight: 2 } ],
  [
    { node: 1, weight: 1 },
    { node: 3, weight: 3 },
    { node: 5, weight: 2 }
  ],
  [ { node: 2, weight: 3 }, { node: 5, weight: 1 } ],
  [ { node: 1, weight: 2 }, { node: 5, weight: 2 } ],
  [
    { node: 2, weight: 2 },
    { node: 3, weight: 1 },
    { node: 4, weight: 2 }
  ]
]

연결된 노드에서의 값이 현재의 값 + 해당 노드의 시간(가중치) 보다 클 경우, 값을 갱신..

arr[node].forEach((next) => {
  if (distance[next.node] > distance[node] + next.weight) {
    distance[next.node] = distance[node] + next.weight;
  }
});

Infinity
Infinity의 초기값은 Number.POSITIVE_INFINITY입니다.
Infinity(양의 무한대)는 다른 어떤 수보다 더 큽니다.

Array.from()
Array.from() 메서드는 유사 배열 객체(array-like object)나 반복 가능한 객체(iterable object)를 얕게 복사해 새로운Array 객체를 만듭니다.
ex)
console.log(Array.from([1, 2, 3], x => x + x));
// expected output: Array [2, 4, 6]

[References]

신장트리 관련 :
https://gmlwjd9405.github.io/2018/08/28/algorithm-mst.html
Dijkstra 관련 :
https://m.blog.naver.com/ndb796/221234424646
https://mattlee.tistory.com/50
Dijkstra Javascript Code 참고 :
https://hackernoon.com/how-to-implement-dijkstras-algorithm-in-javascript-abdfd1702d04

기록중

이전 포스트

AWS lambda

다음 포스트

MST & Dijkstra Algorithm

신장트리 (Spanning Tree)

MST(Minimum Spanning Tree)

MST의 특징

MST의 구현 방법

Kruskal MST 알고리즘

Prim MST 알고리즘

Dijkstra Algorithm

Dijkstra 활용 문제

AWS lambda

MST & Dijkstra Algorithm

0개의 댓글