Confidence Intervals and Hypothesis testing - Week 4

Lesson 1 - Confidence Intervals

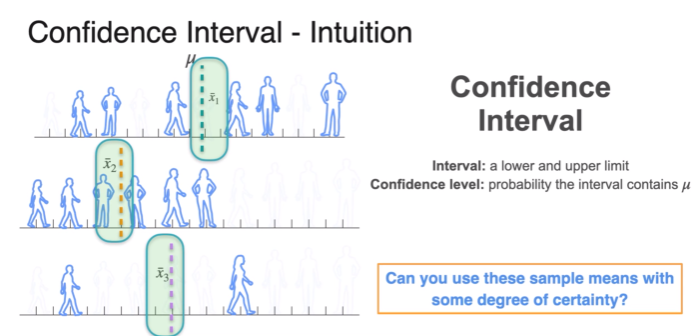
Confidence Intervals - Overview

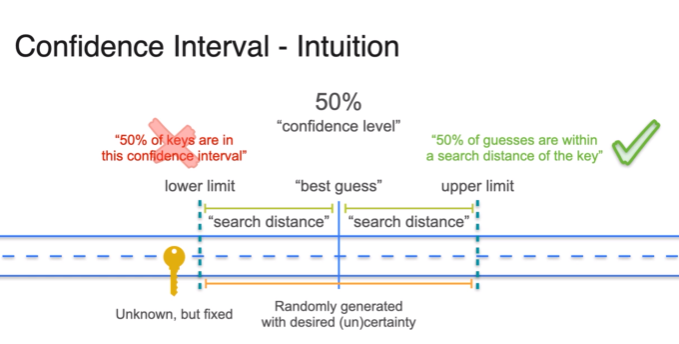
• 신뢰구간 50% $not equal$ 50% key가 in the intervals

• True value $\mu$ is the key

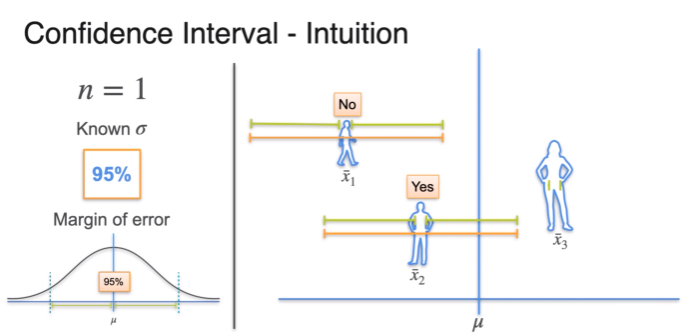
• he drew the $\mu$ but we never know that $\mu$
• we will generate confidence intervals

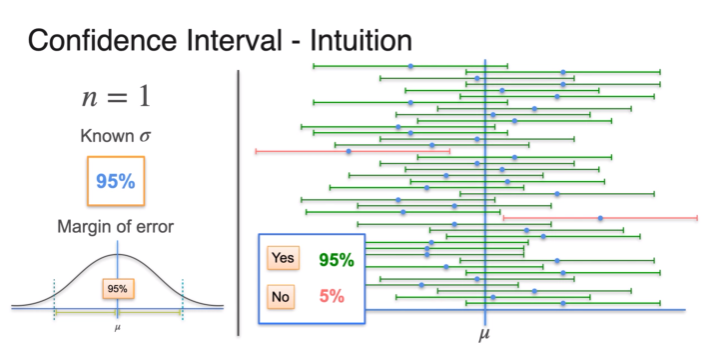
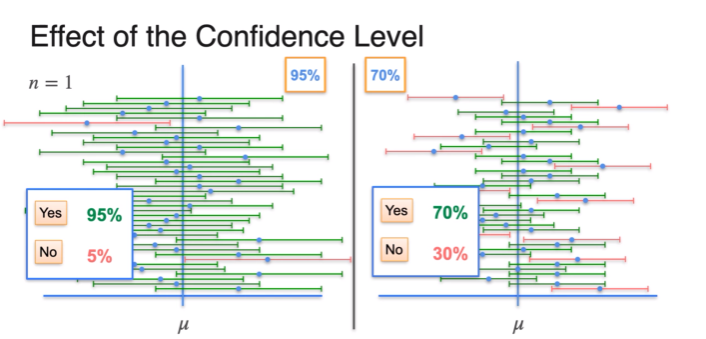
Confidence Intervals - Changing the Interval

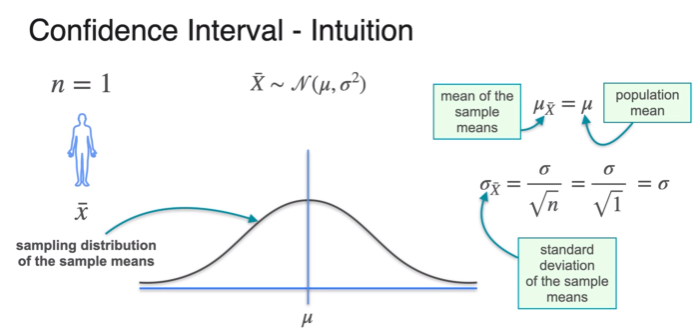
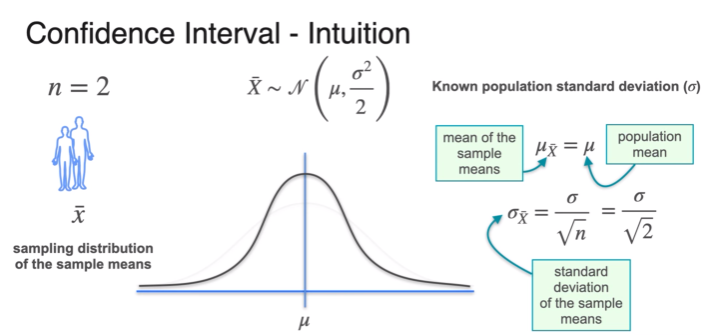
• standard deviation depends on sample size

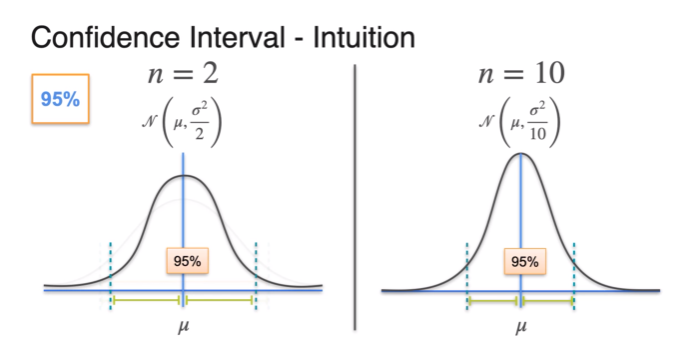
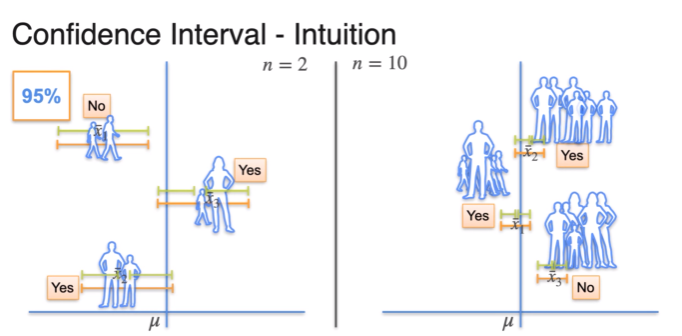
• more sample, smaller margin of error

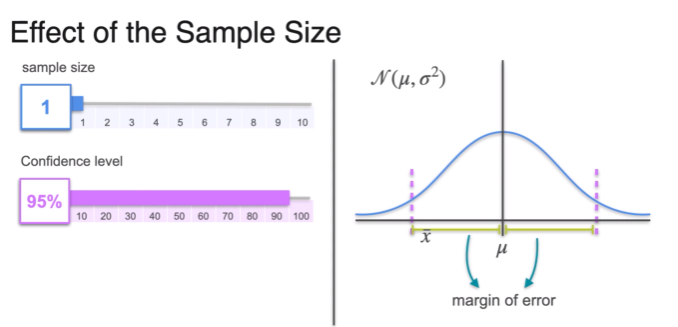
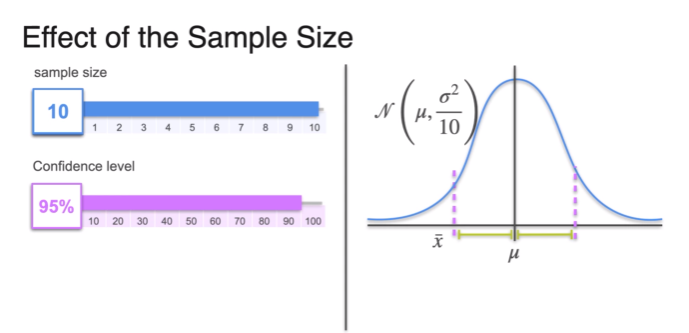
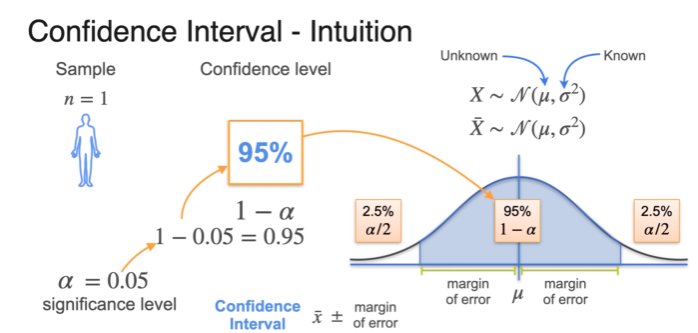
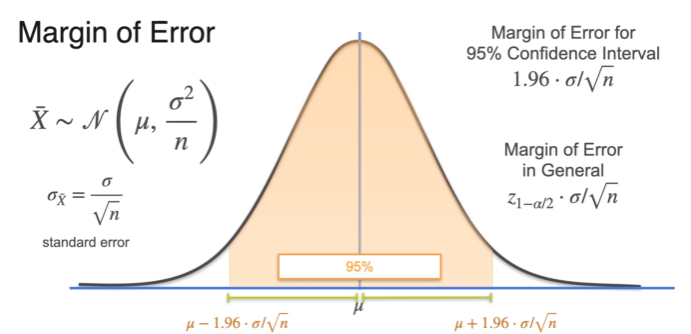
Confidence Intervals - Margin of Error

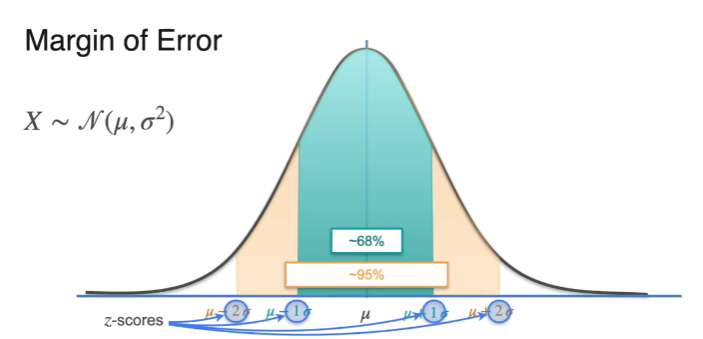
• z-score; Z distribution

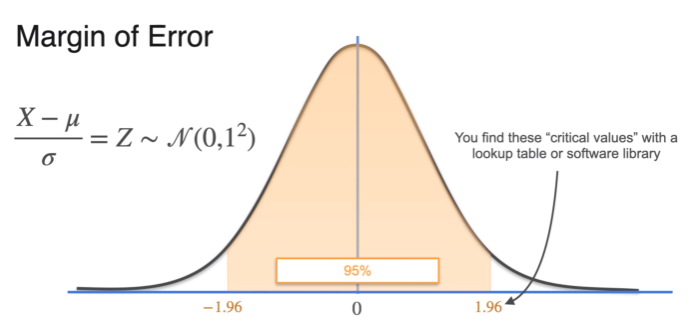
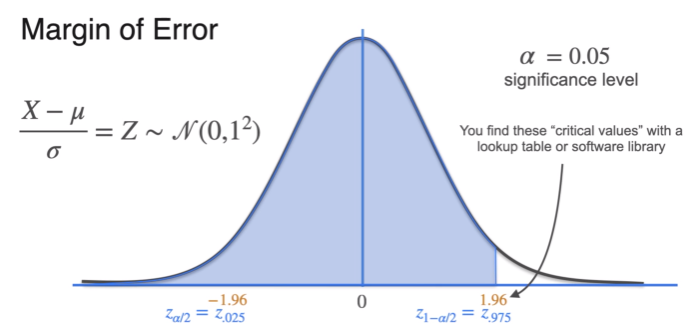
• confidence interval at 90%
• significance level $\alpha$ = 0.1
• between $Z_{a/2}$ and $Z_{1-a/2}$

Confidence Intervals - Calculation Steps

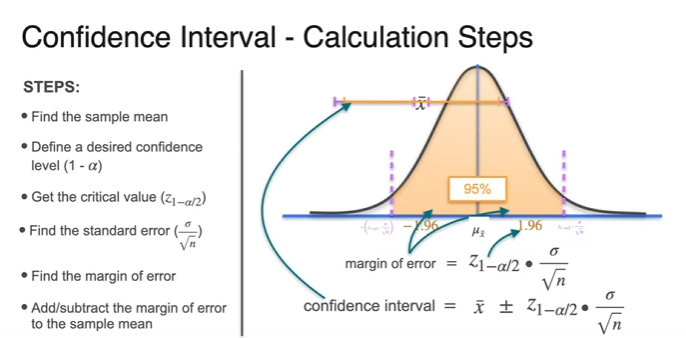
• confidence interval = $\tilde{X} \pm Z_{1-a/2}*\frac{\sigma}{\sqrt{n}}$

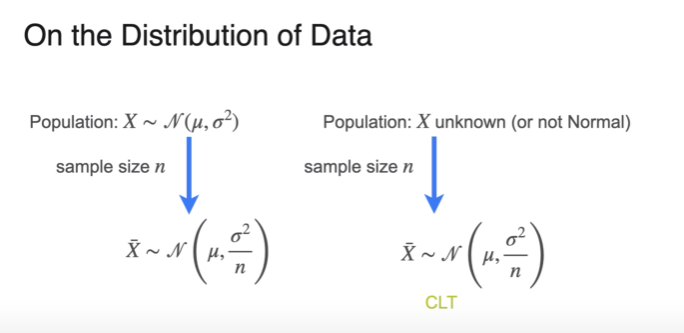
• Assumptions

  • simple random sample
  • sample size > 30 or popuilation is approximately normal

Confidence Intervals - Example

Calculating Sample Size

• 역산inverse operation

Difference Between Confidence and Probability

• but sample mean

Unknown Standard Deviation

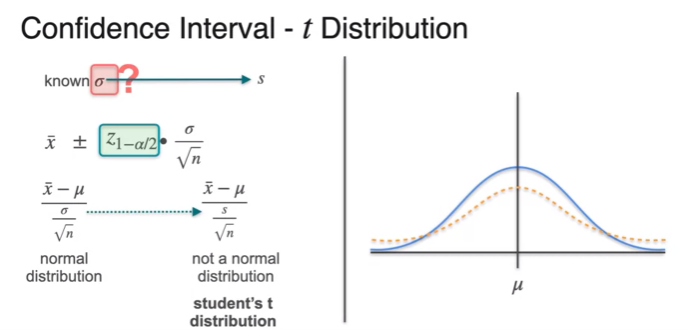
• as we don't know the real $\sigma$

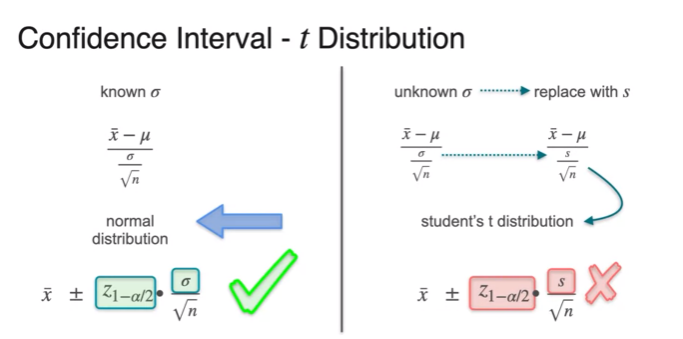
• it's wrong because it depends on normal distribution
  • scaling issue

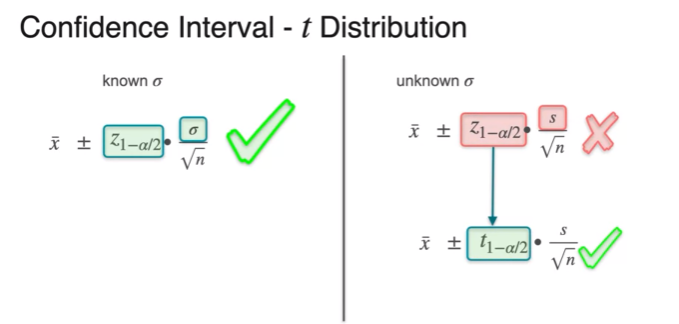
• use student $s$ instead of $\sigma$ and $t$ instead of $z$

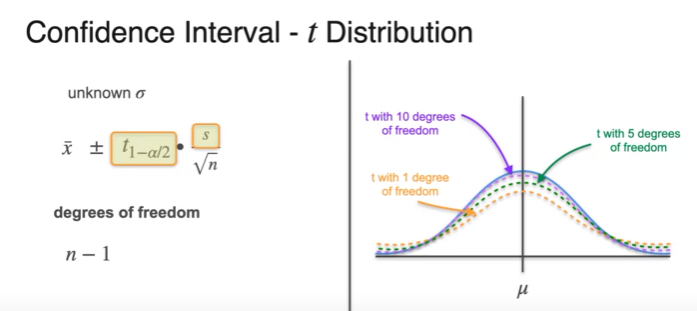
• the more sample you use $s$ getting closer to $\sigma$ also sample distribution and normal distribution is
• degrees of freedom

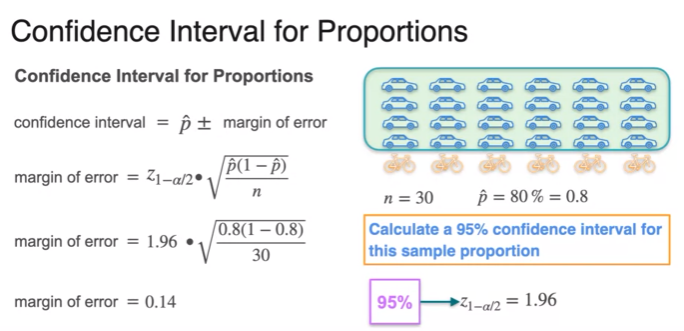
Confidence Intervals for Proportion

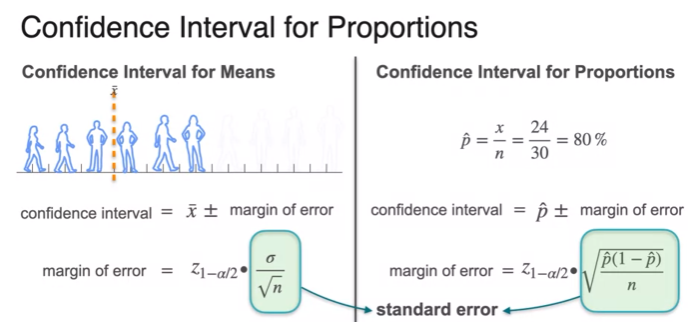
Lesson 2 - Hypothesis Testing

Defining Hypotheses

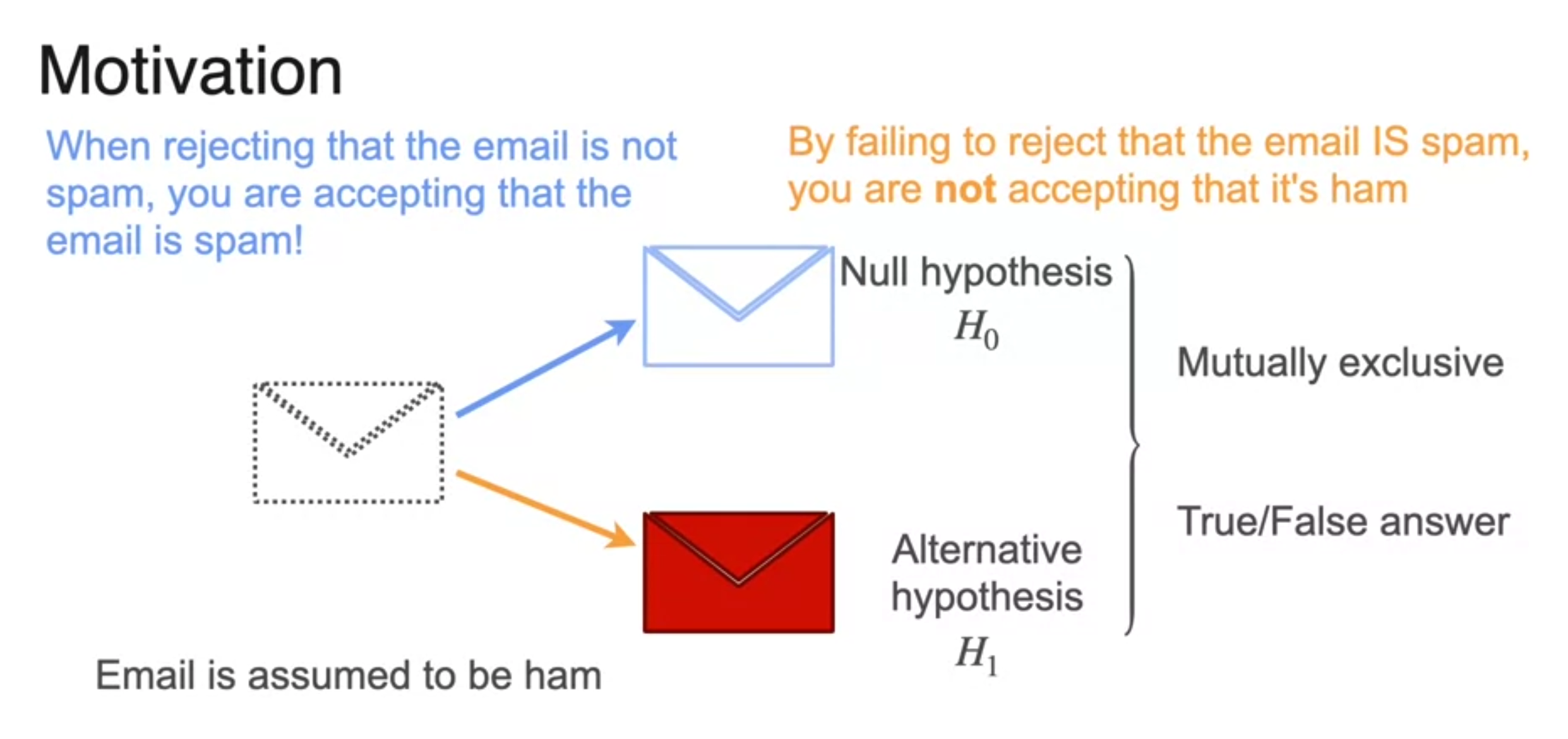
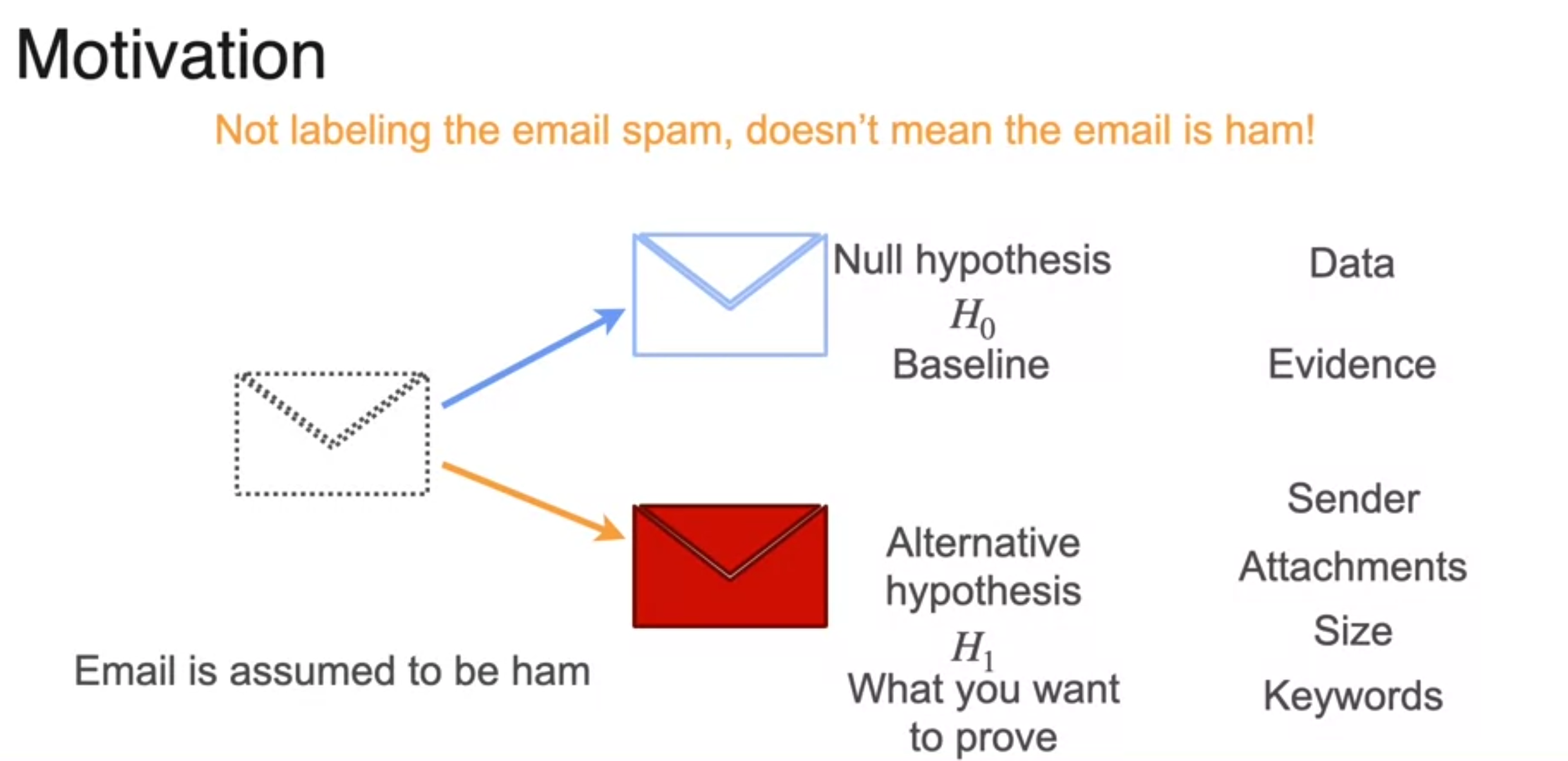
• base assumption - avoid risk

Type I and Type II errors

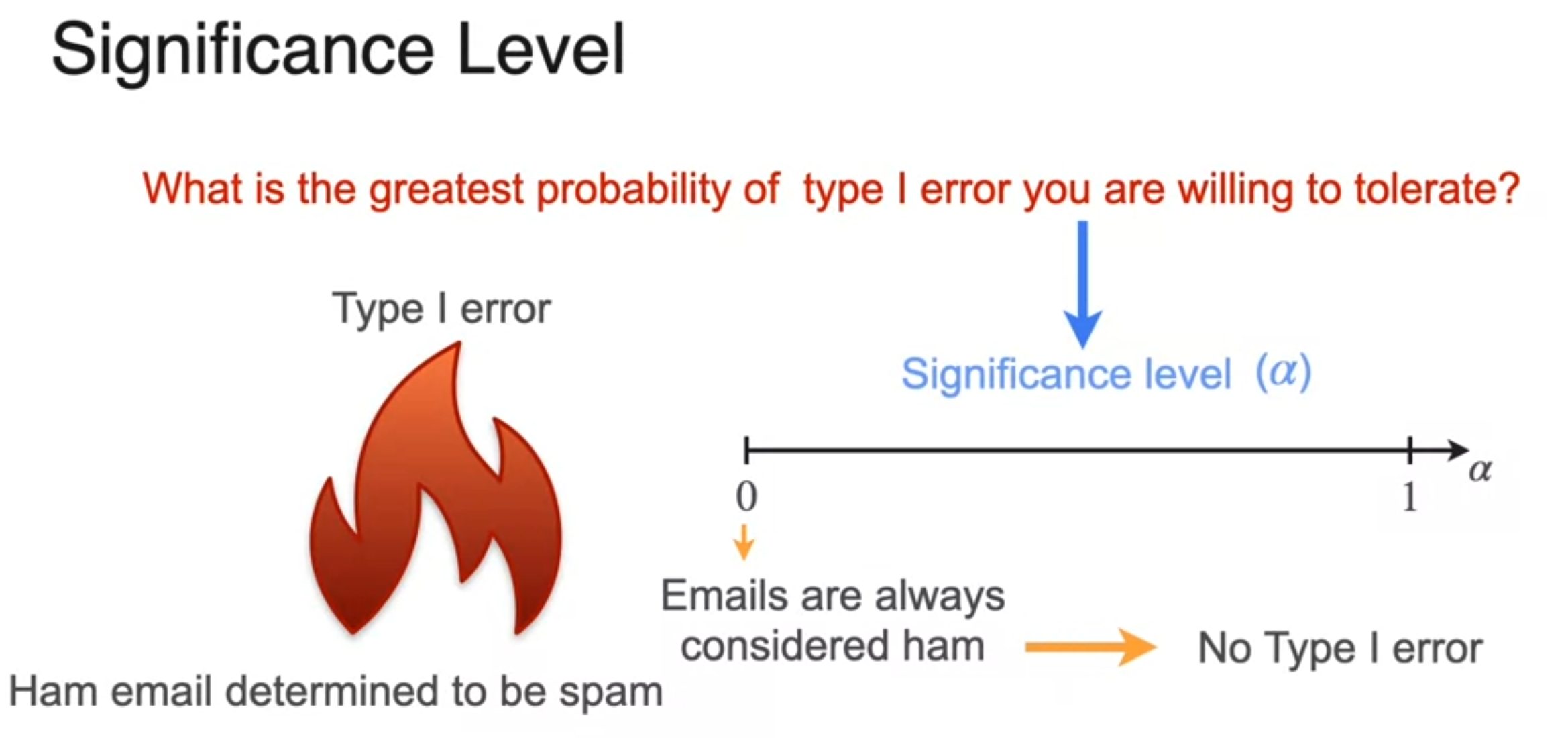
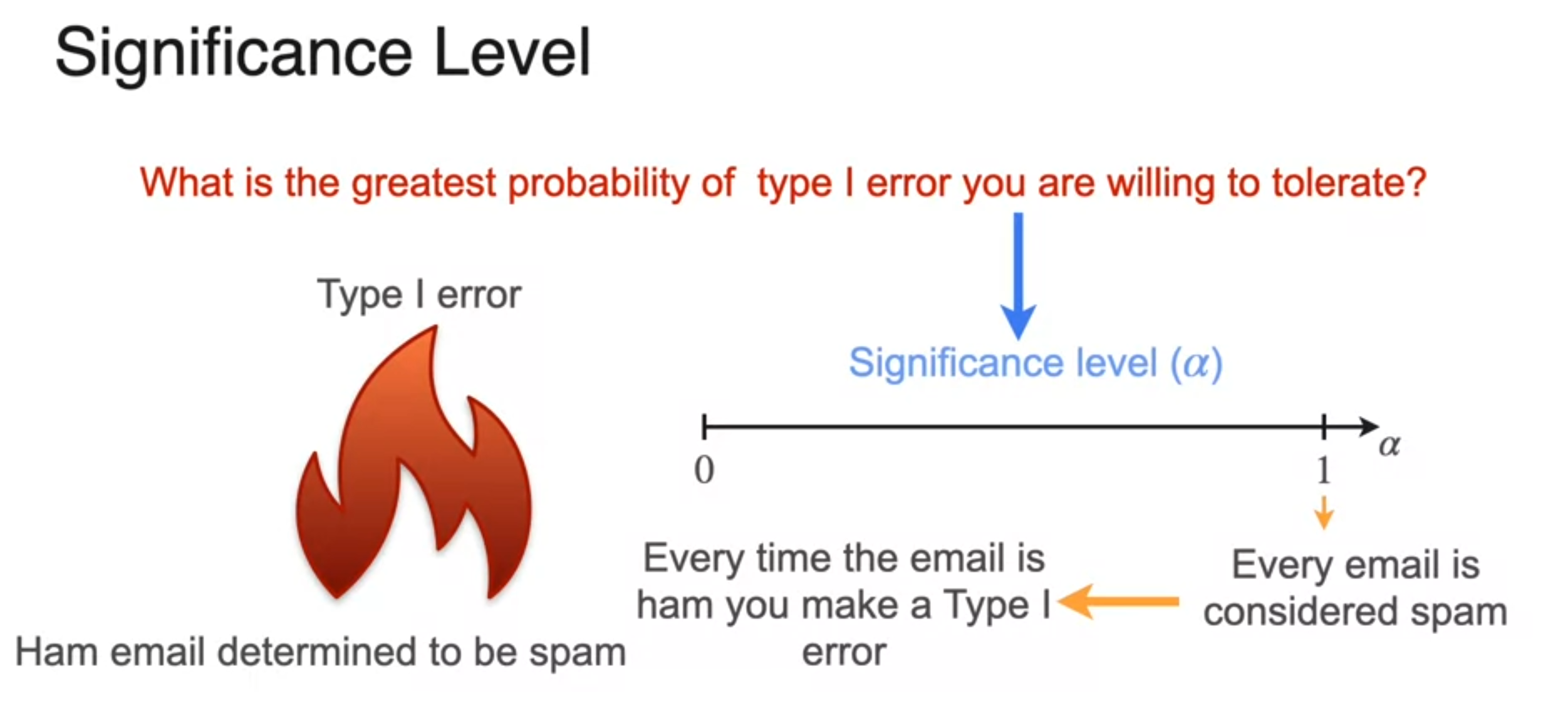
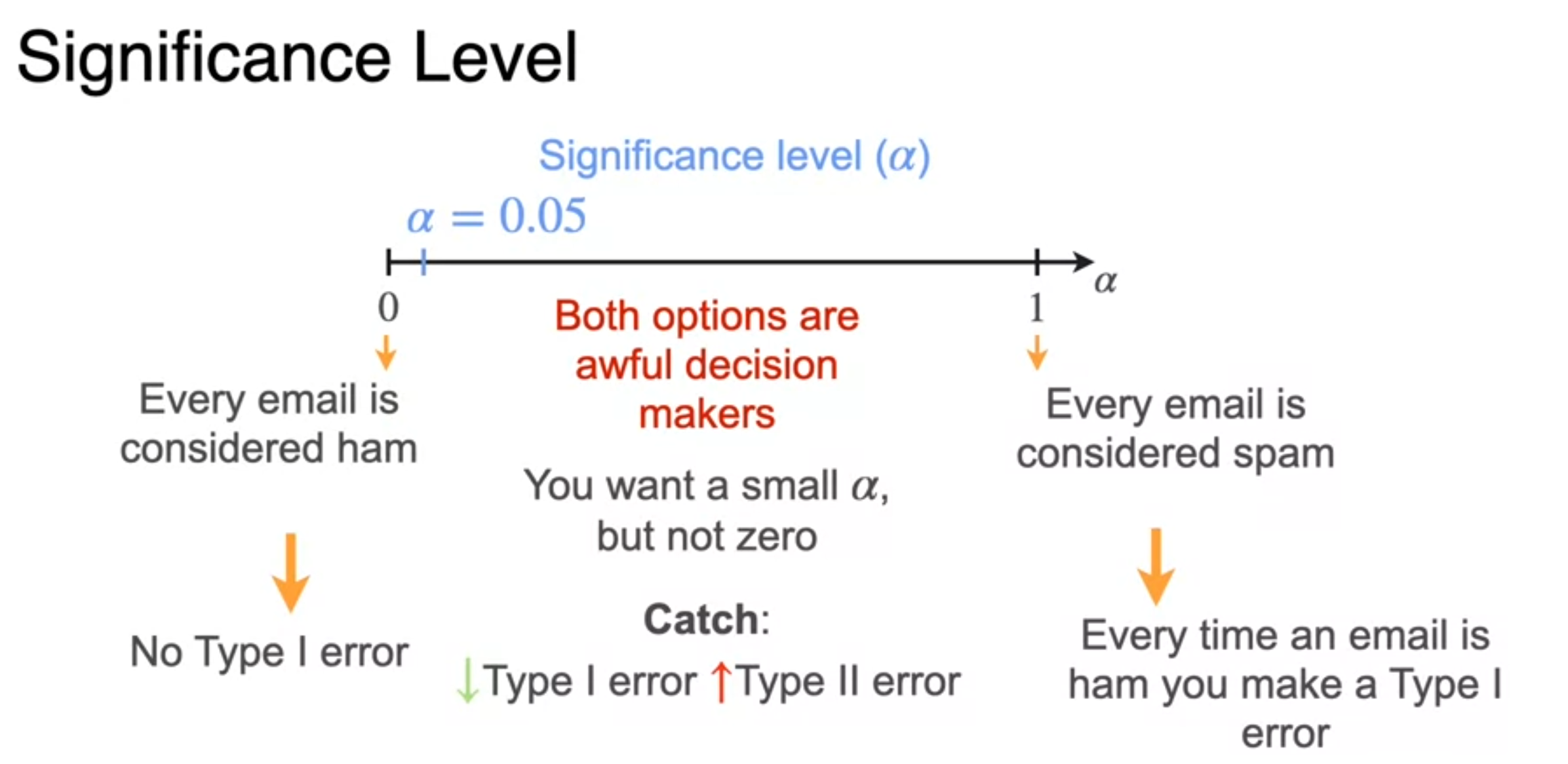
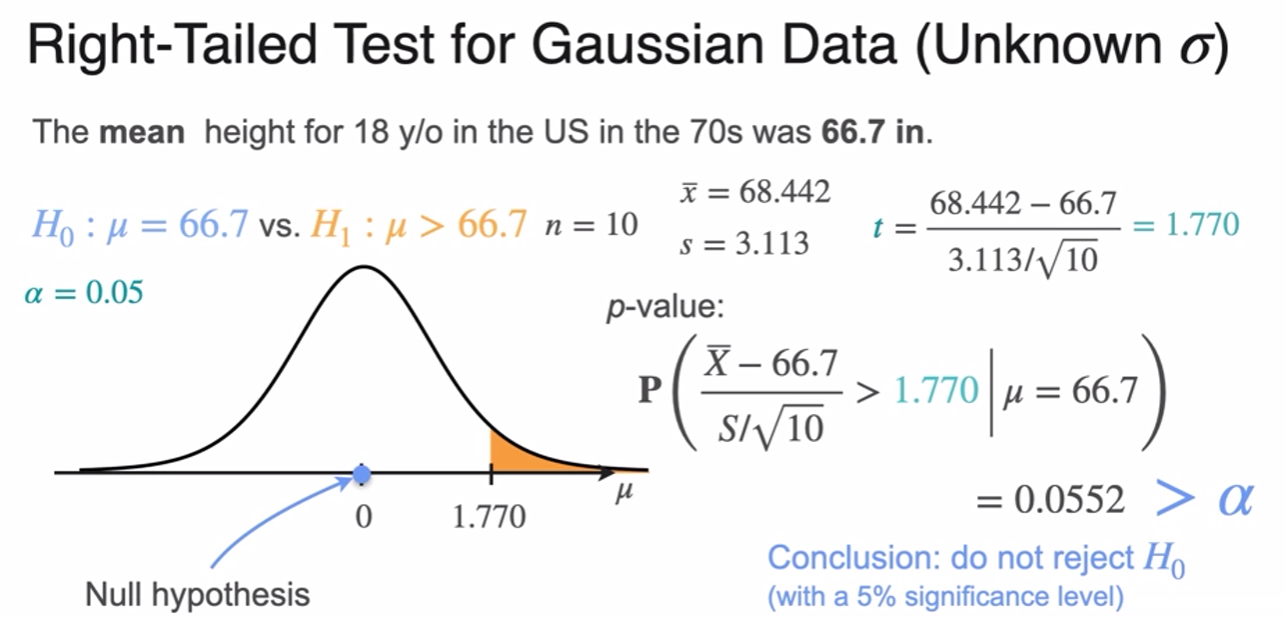
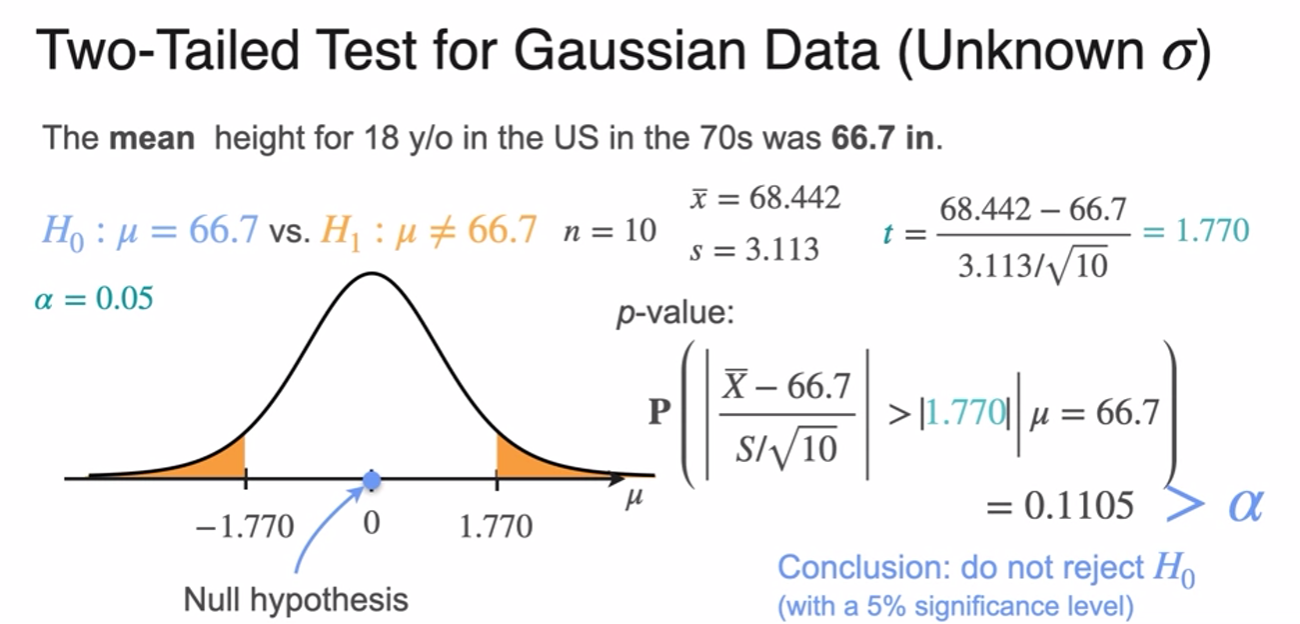
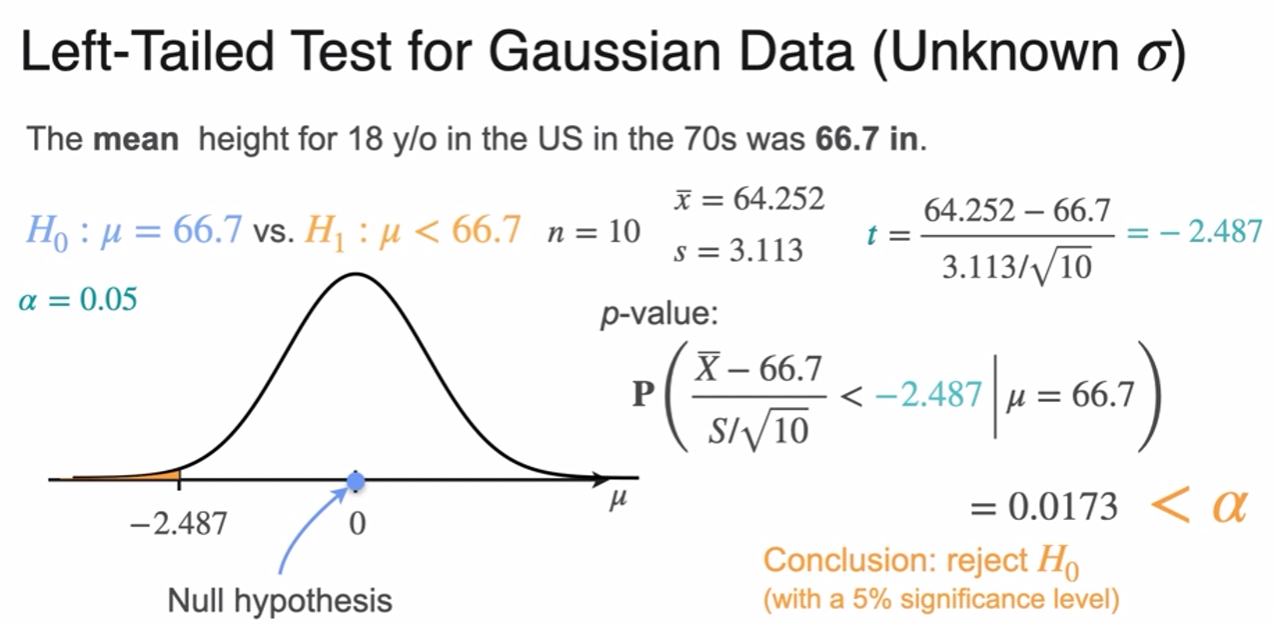
Right-Tailed, Left-Tailed, and Two-Tailed Tests

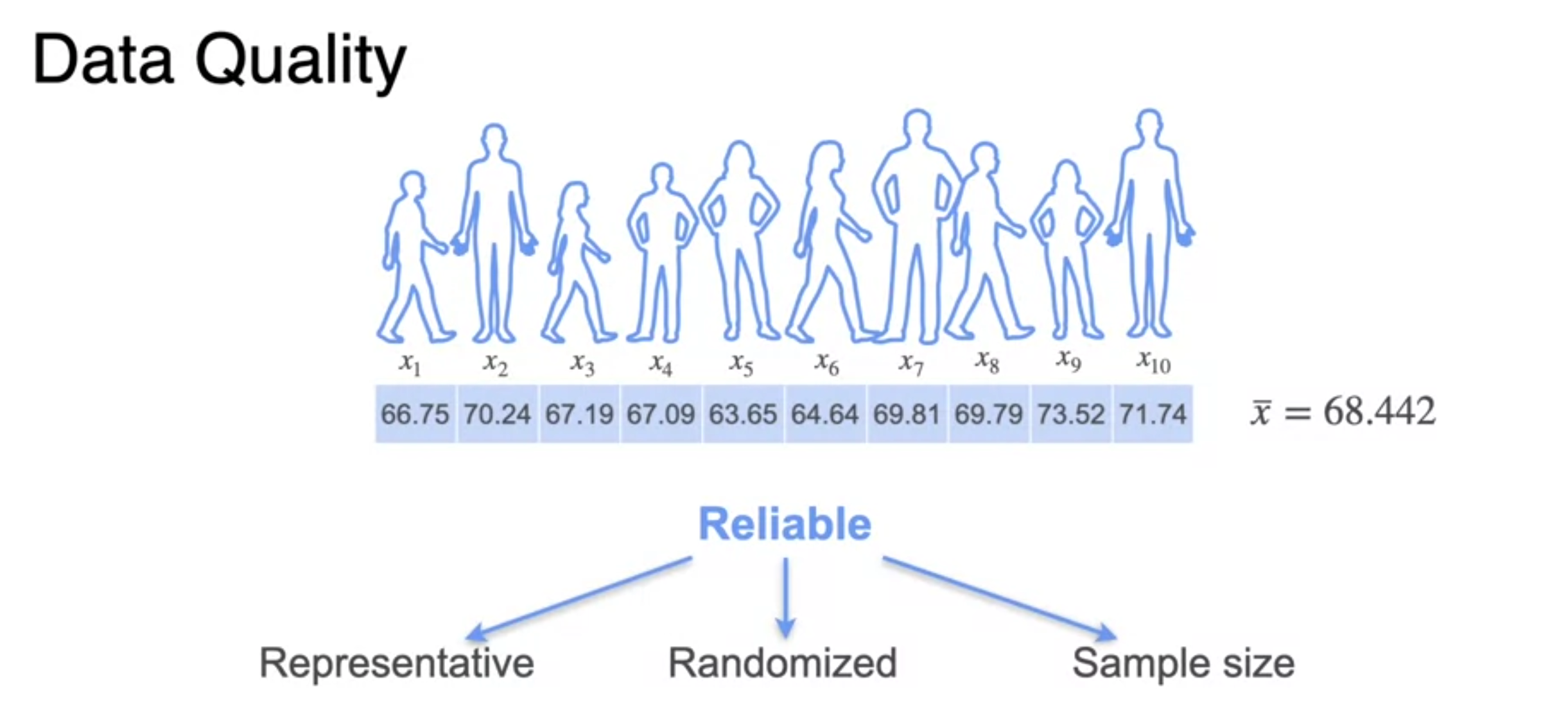
• Representative
• Random
• Sample size (normally over 30)

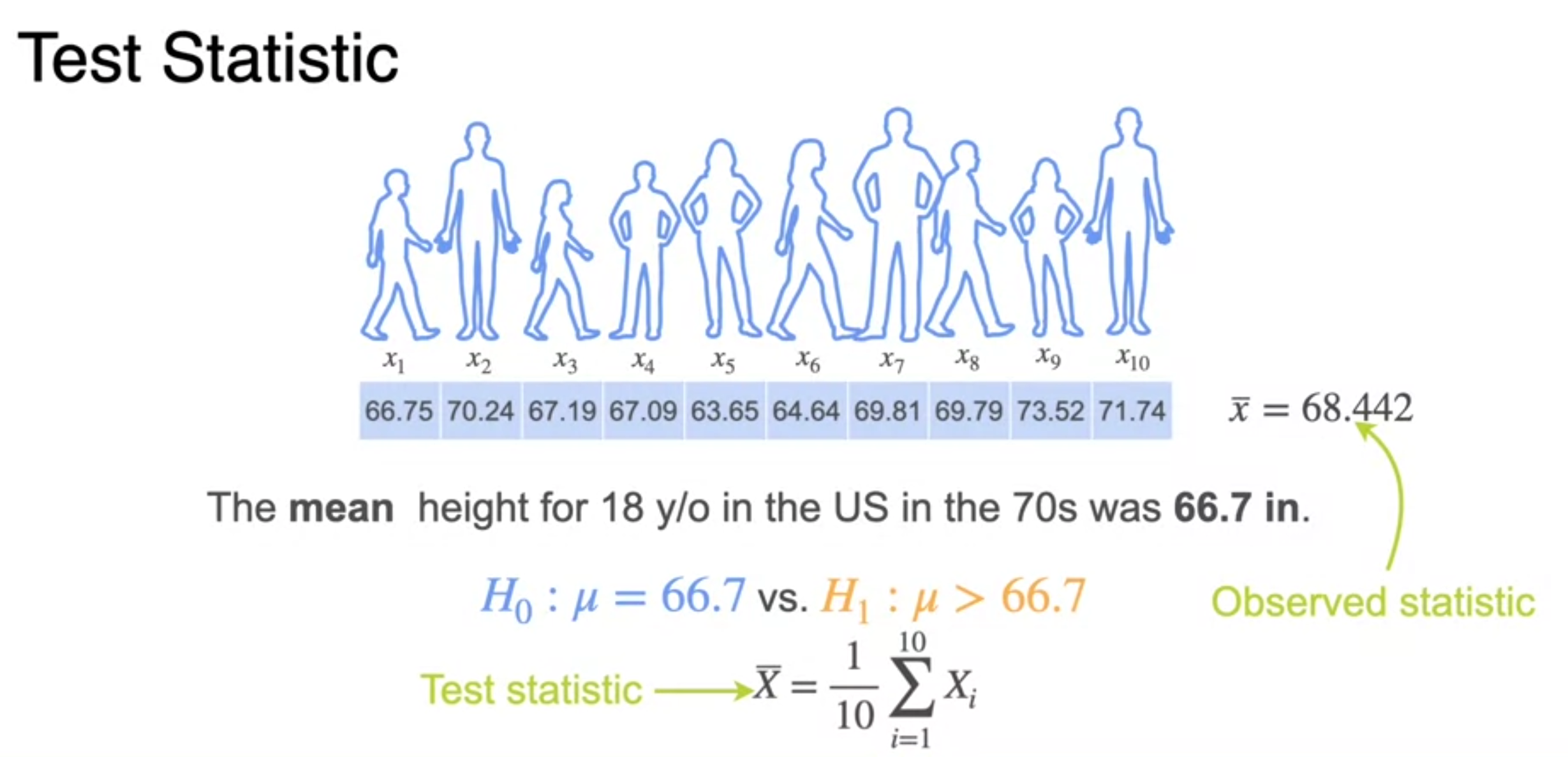
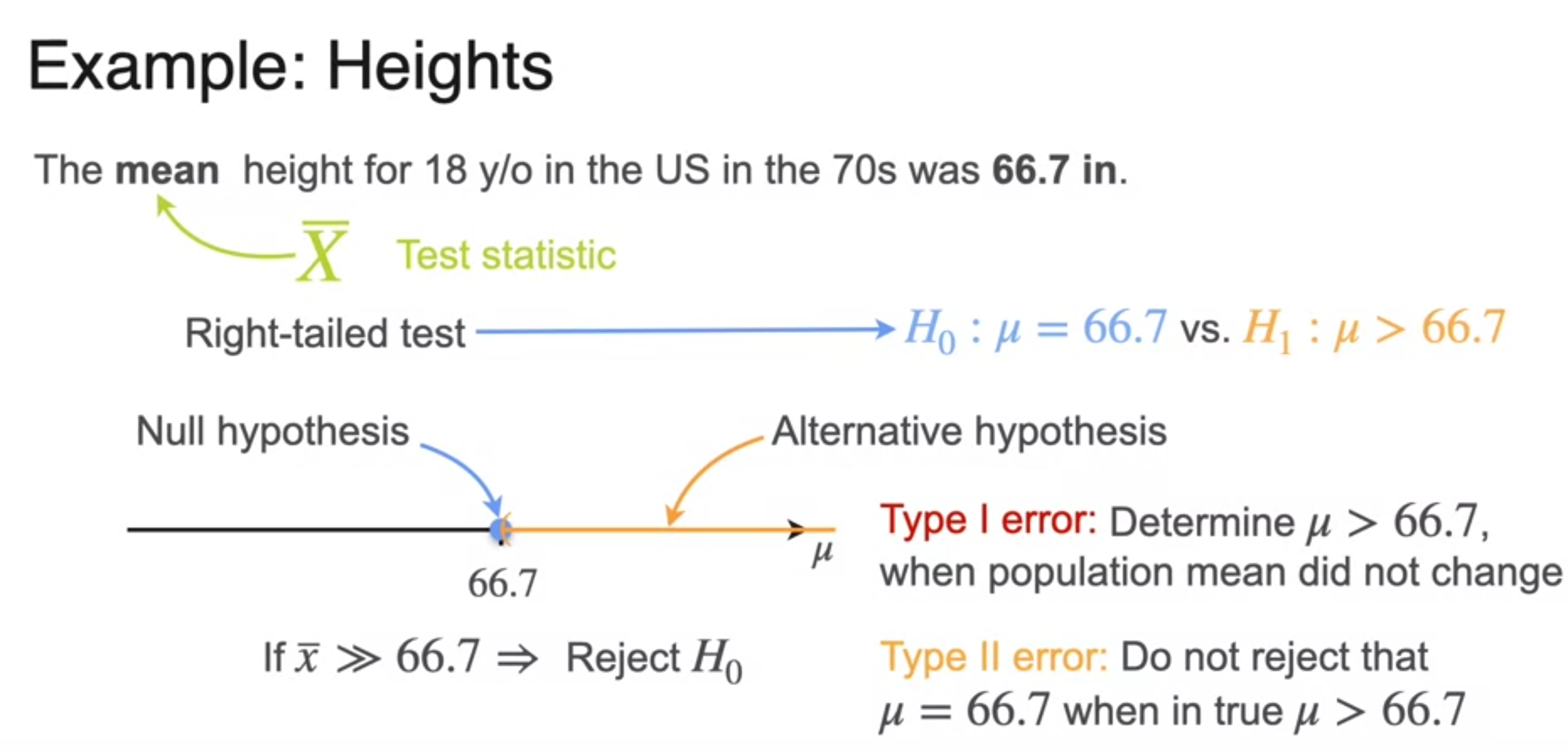
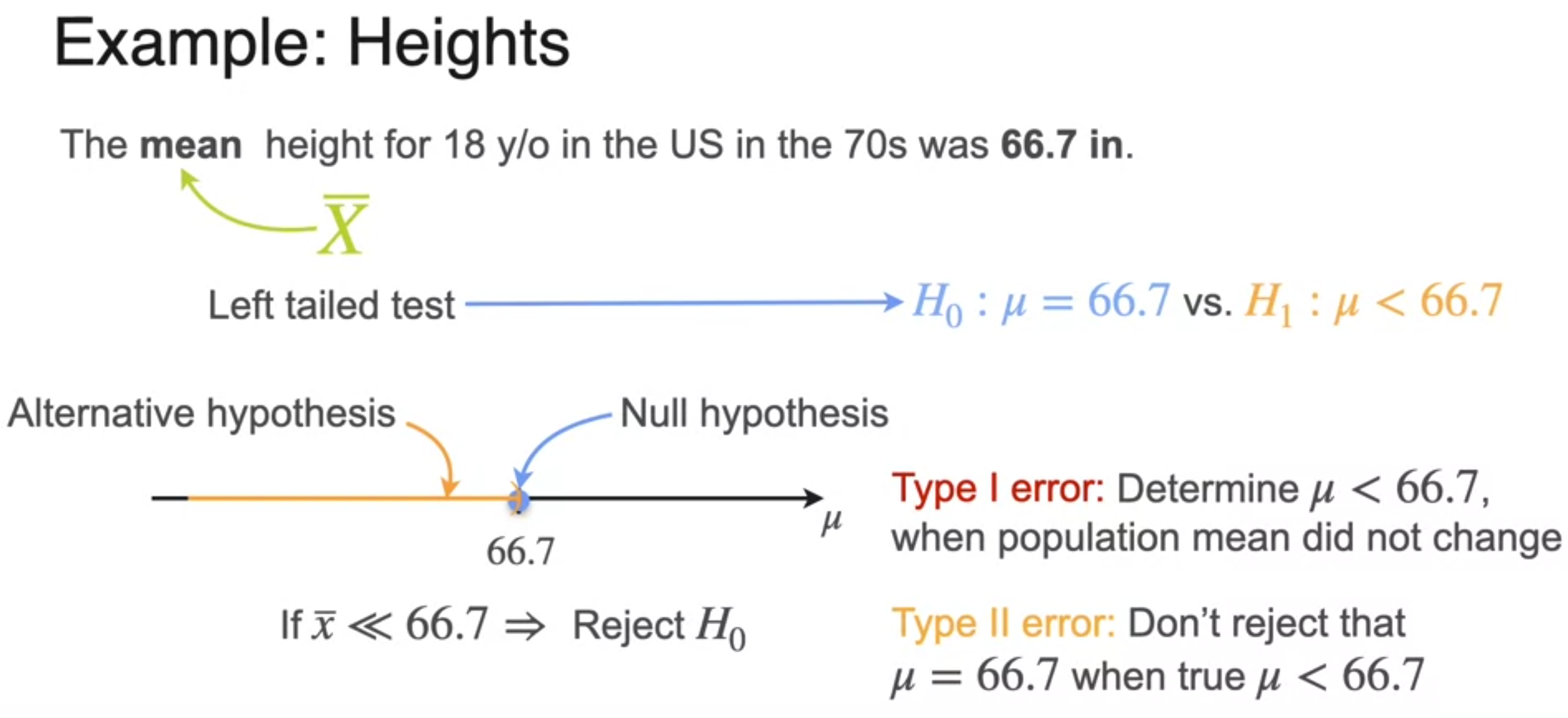
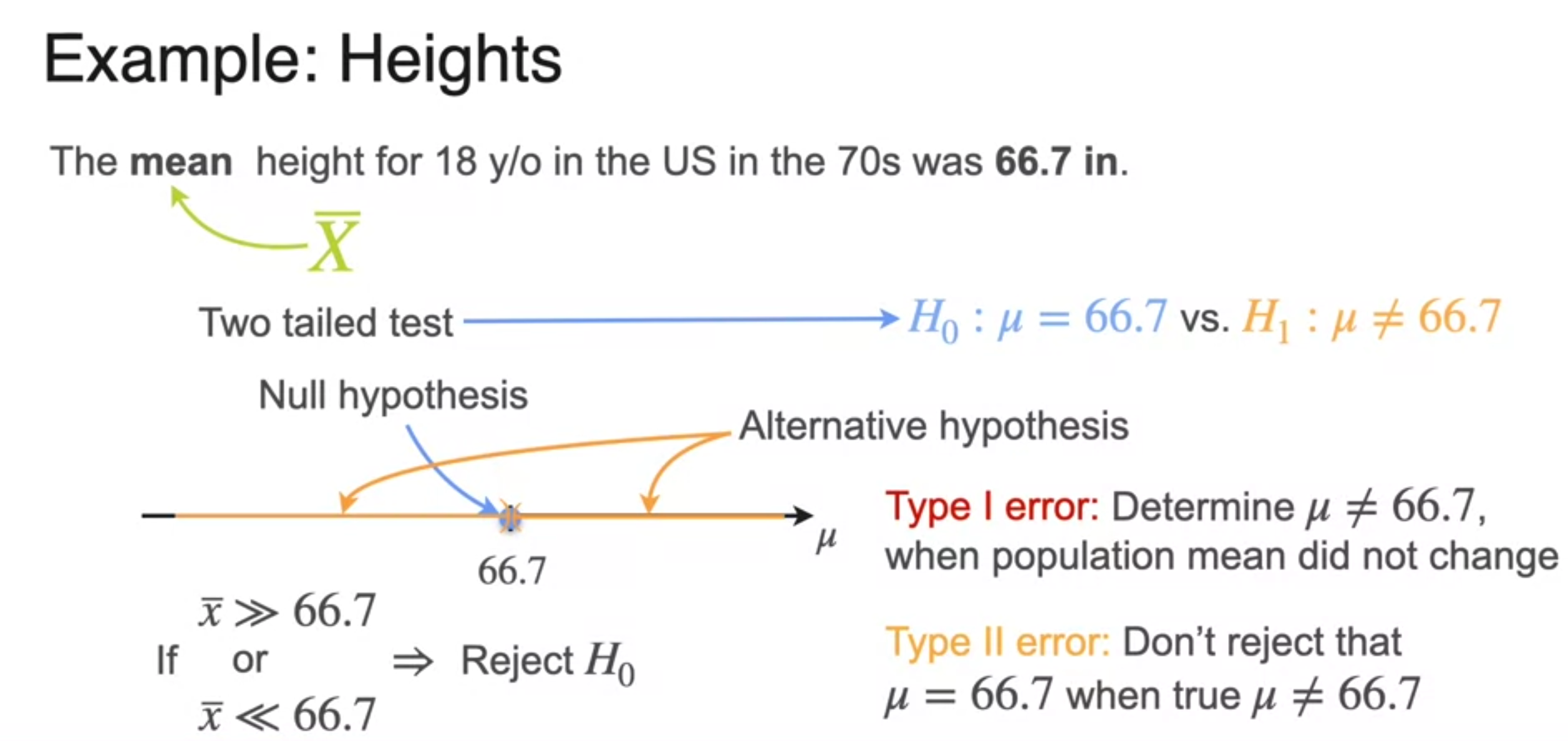
p-Value

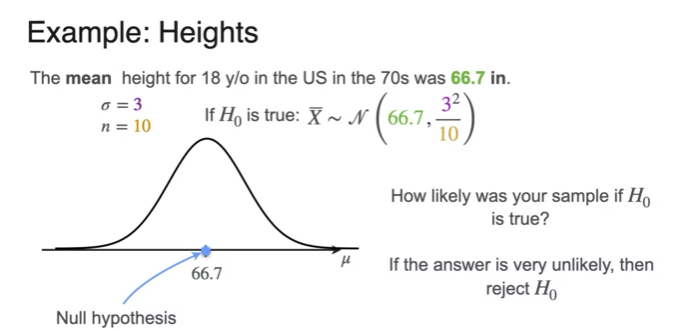
• p-value유의확률
  • 너무 작으면 귀무가설 거절(0.05, 근래에는 0.005로 조정 권고)

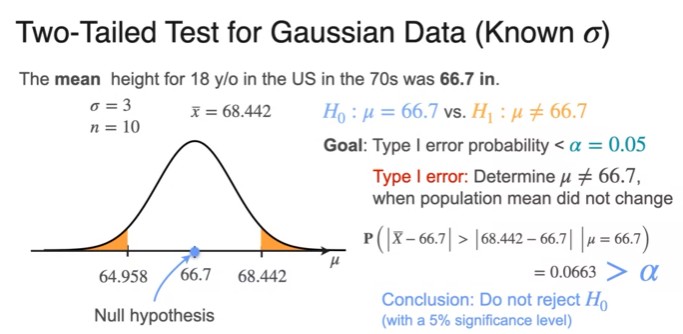
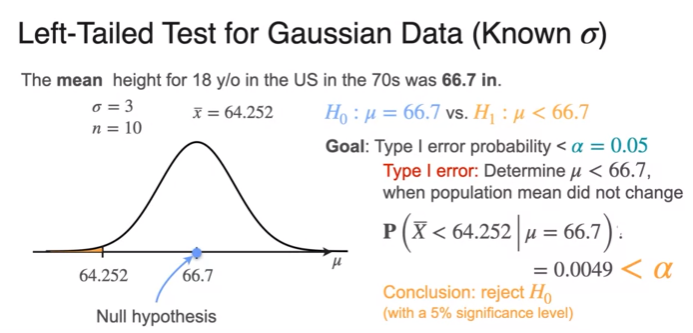
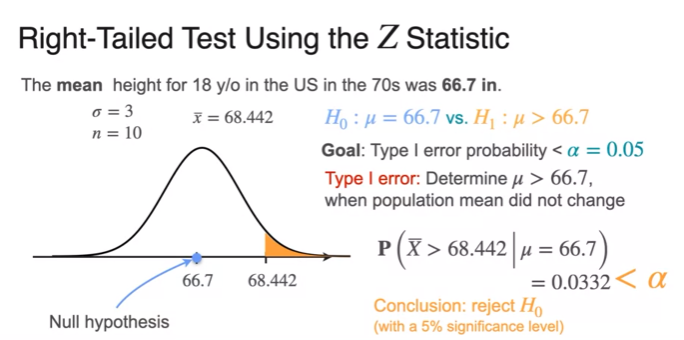
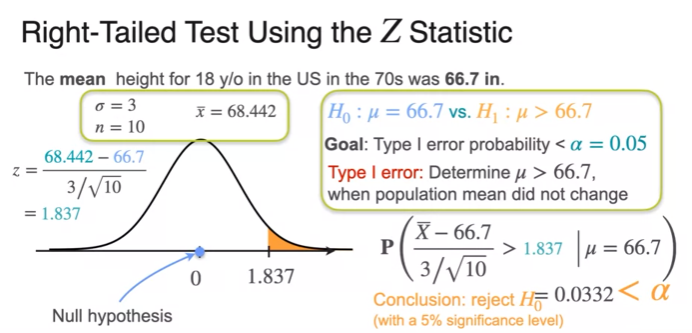
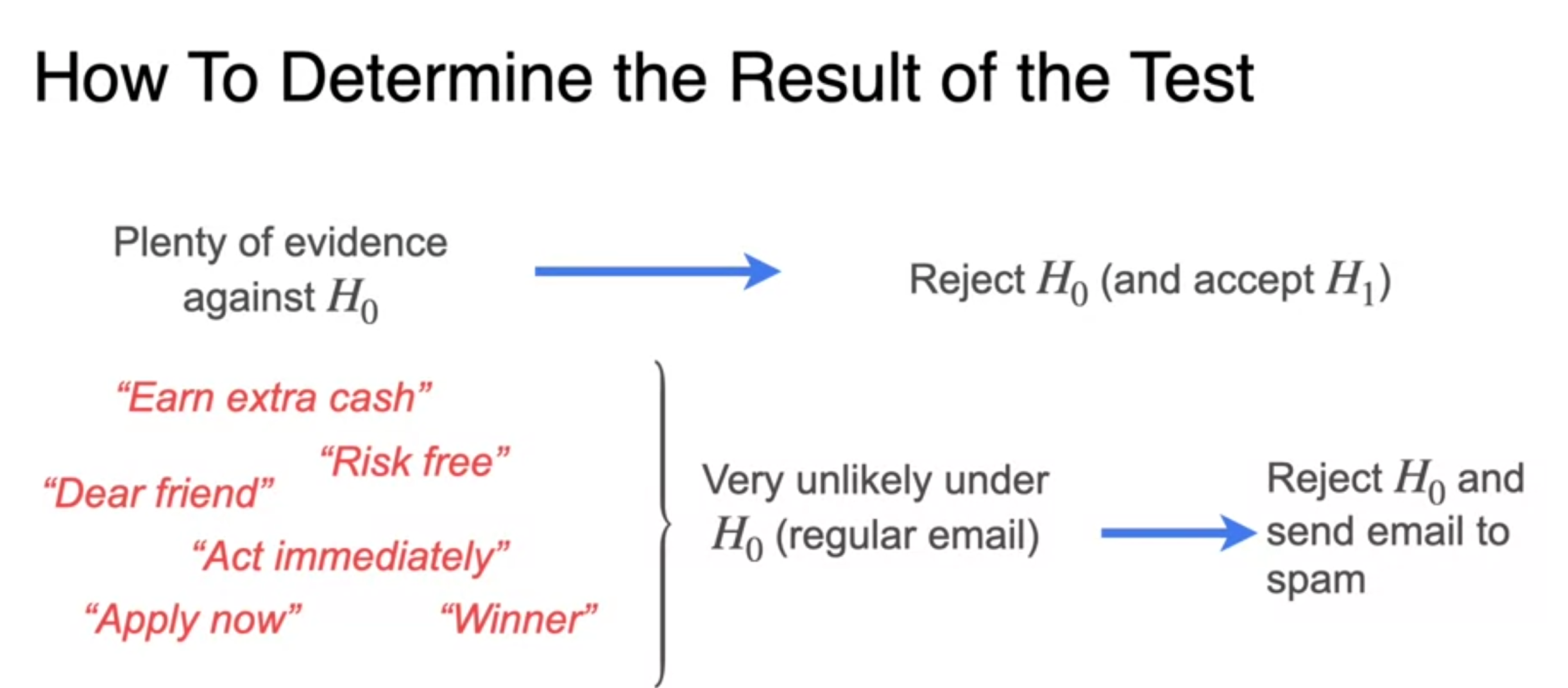
Critical Values

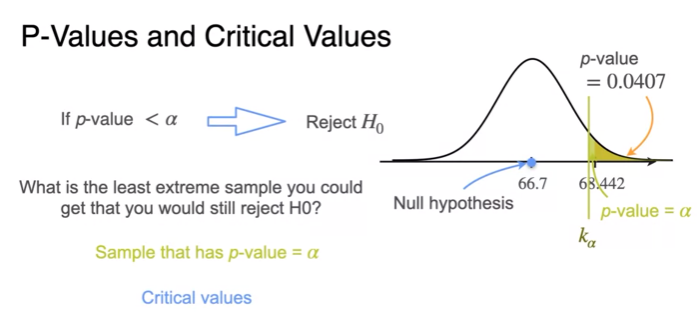
• p-value is smaller than significant level $\alpha$
  • reject $H_0$
• p-value = $\alpha$
  • Critical value

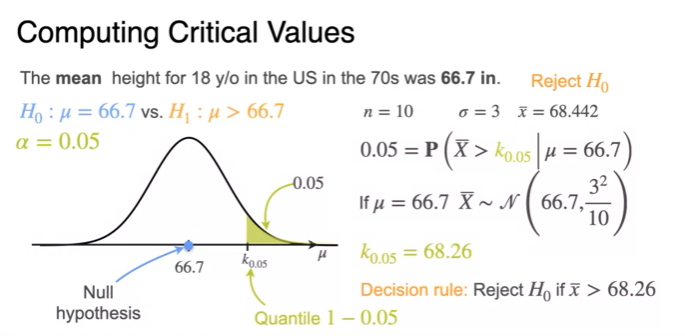
• can reject

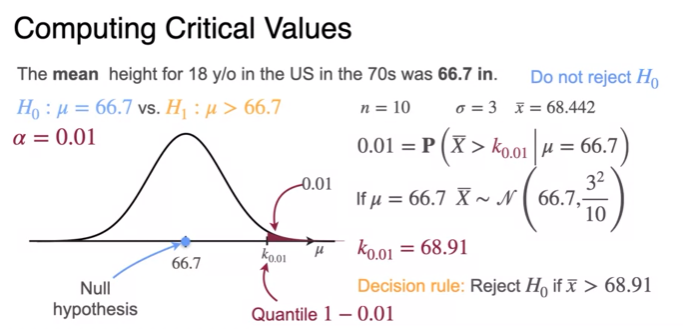
• can not reject

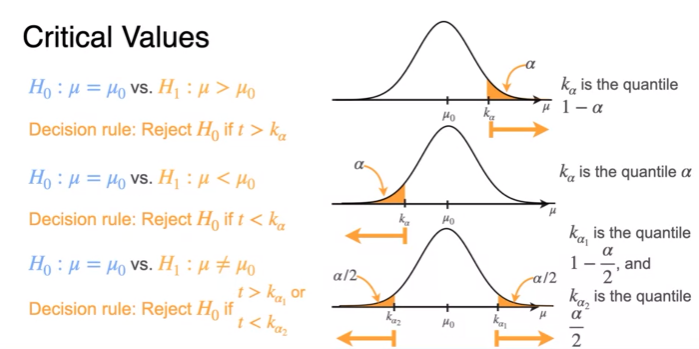
• quantile분위수(절단점)

Power of a Test

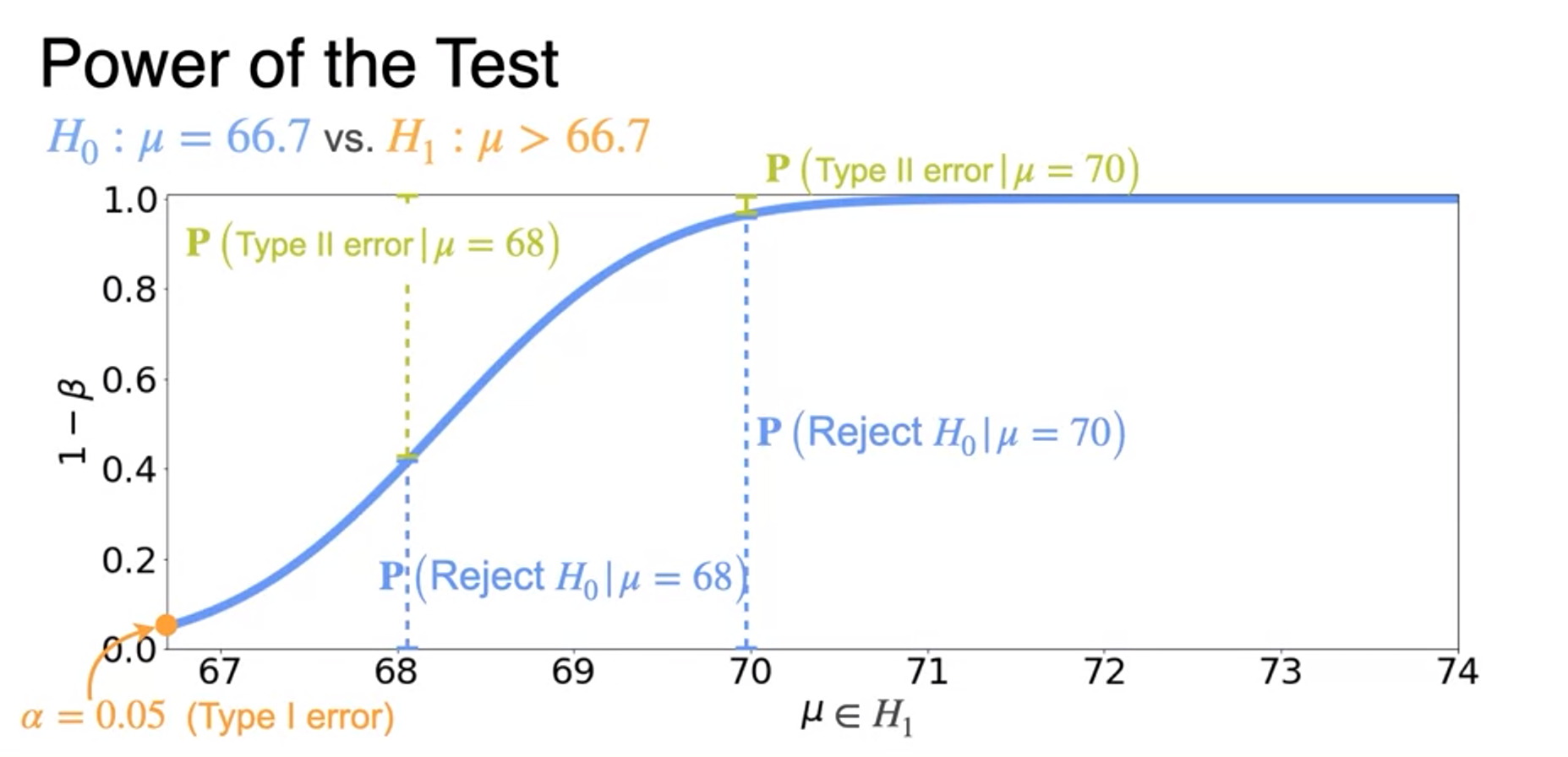
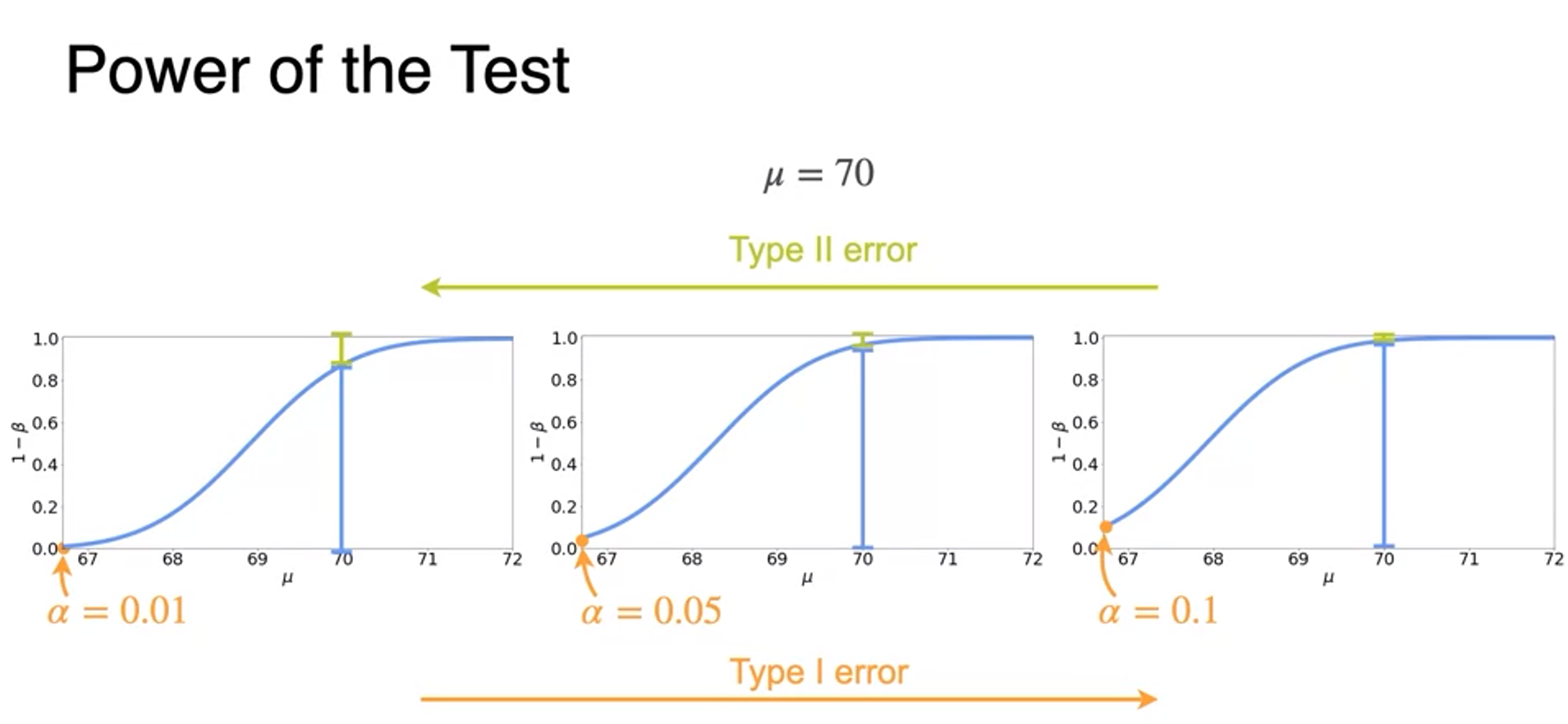
• recall재현율
  TP / TP + FN(type2 error)
  실제로 사실인 것 중에 모델이 사실이라고 한 비율
  모델 정확도가 높을수록 상승
• precision정밀도
  TP / TP + FP(type1 error)
  모델이 사실이라고 한 것 중에 실제로 사실인 비율

Interpreting Results

• for a fixed sample size, the type 1 and type 2 error probabilities are entangled.

• small p-value rejects null hypothesis doesn't represent the probability that the hypothesis is true
• p-value represent seeing the observed data by chance

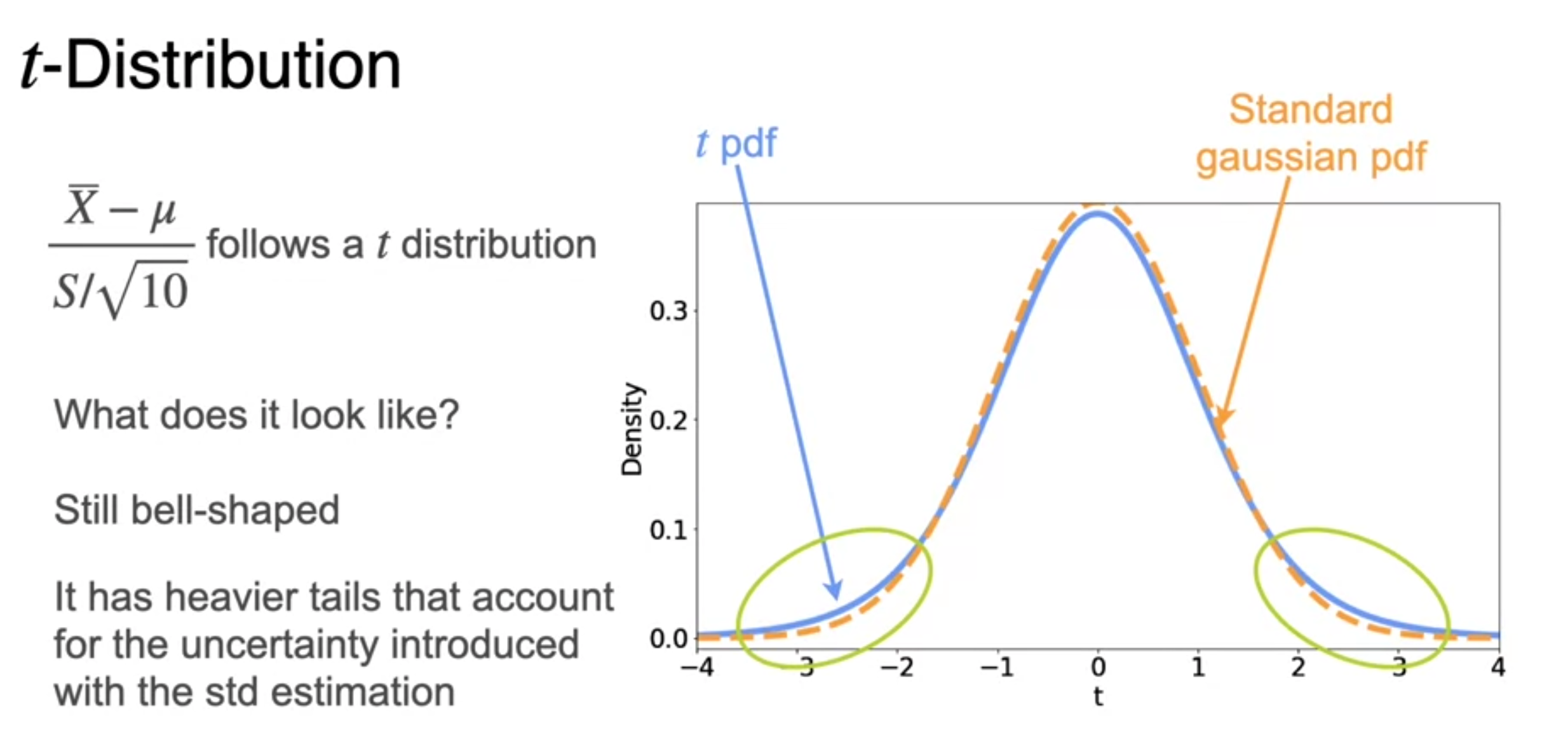
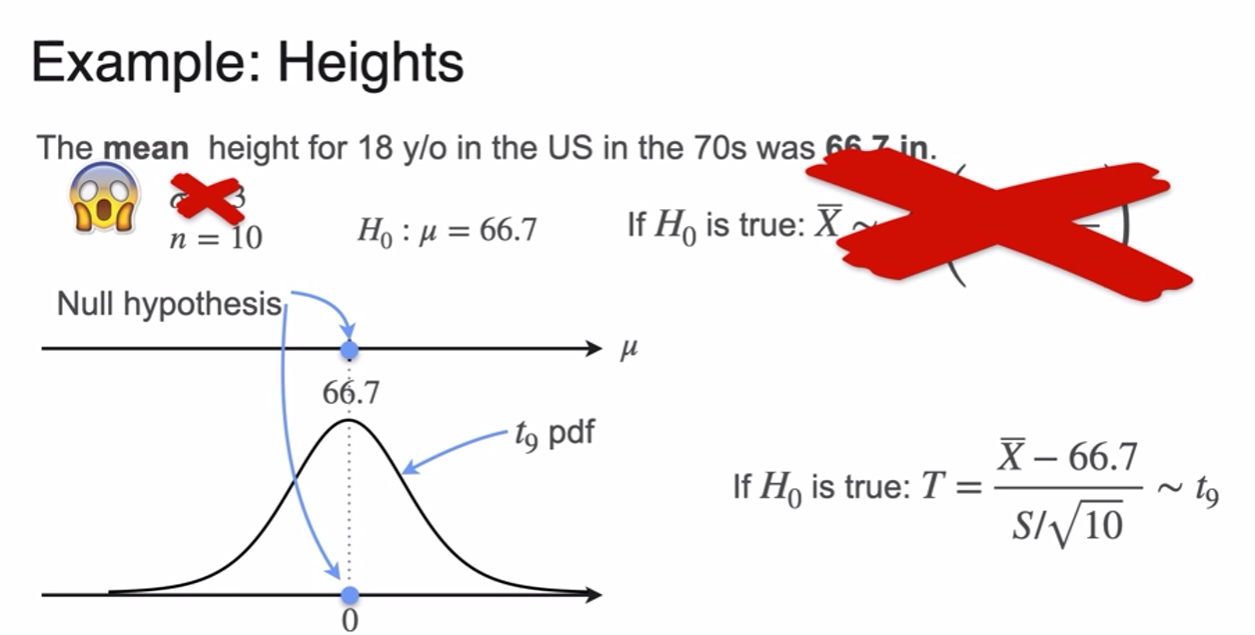
t-Distribution

• you don't actually know sigma
  • replace the sigma in the standardization formula by its estimate S
  • S is almost variance of sample except you divide it by n-1
  • but it follow t-distribution not normal distribution

• $\nu$ as the degrees of freedom increases

• when $\nu$ is near 30 the Gaussian PDF and the TPF looks almost alike

  • that's why we take 30 samples because t-distribution and the Gaussian are very similar

t-Tests

Two Sample t-Test

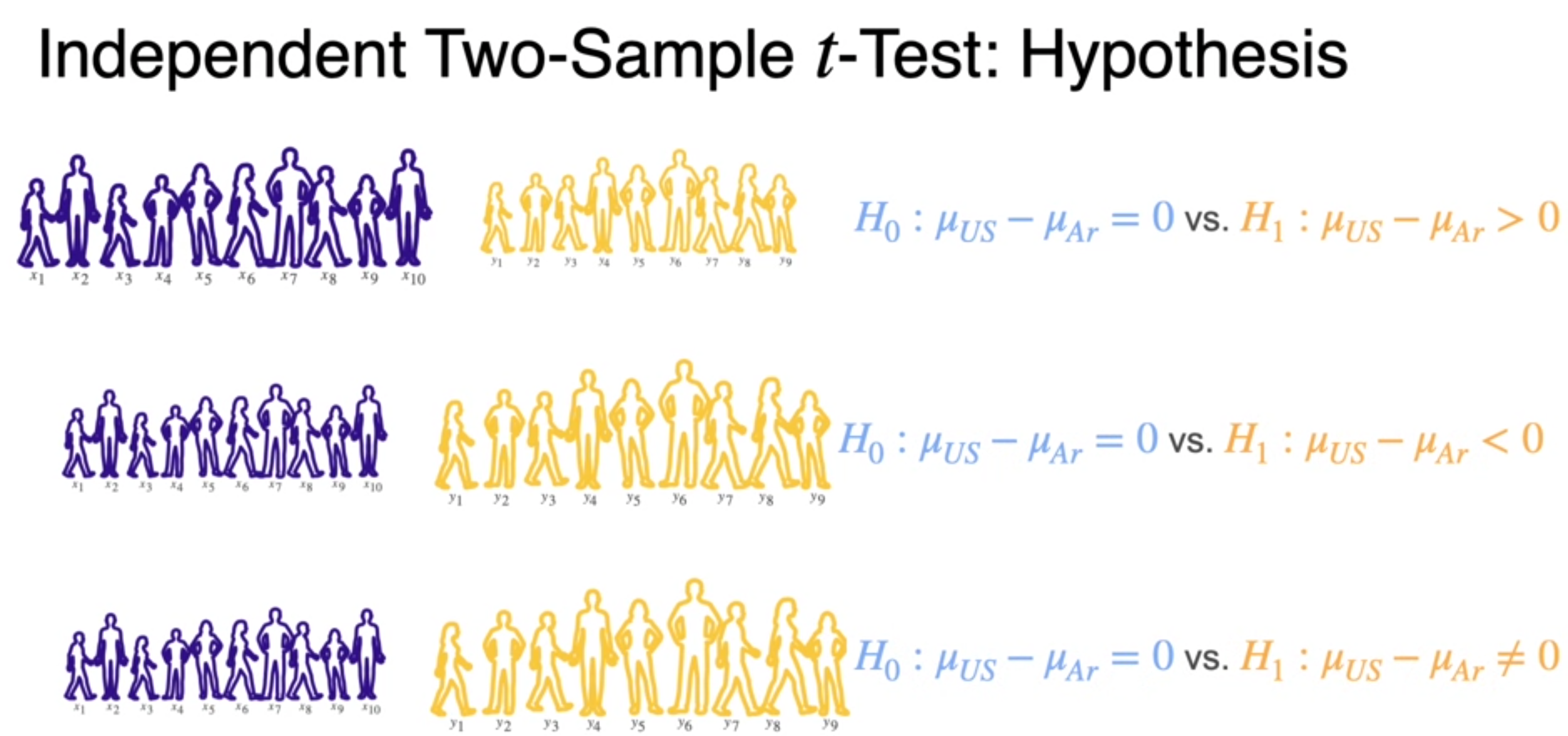
• uses difference between population means

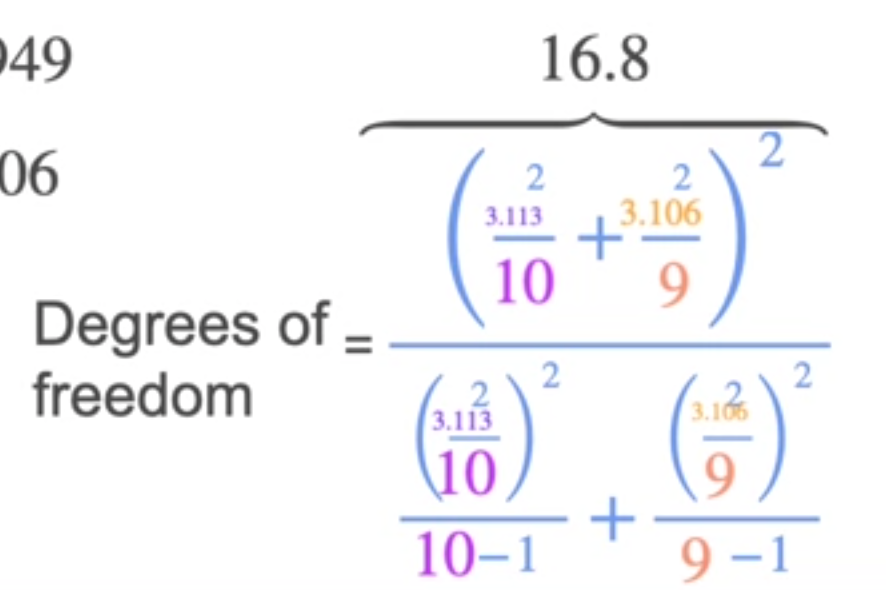
• very complicated Degrees of freedom calculation

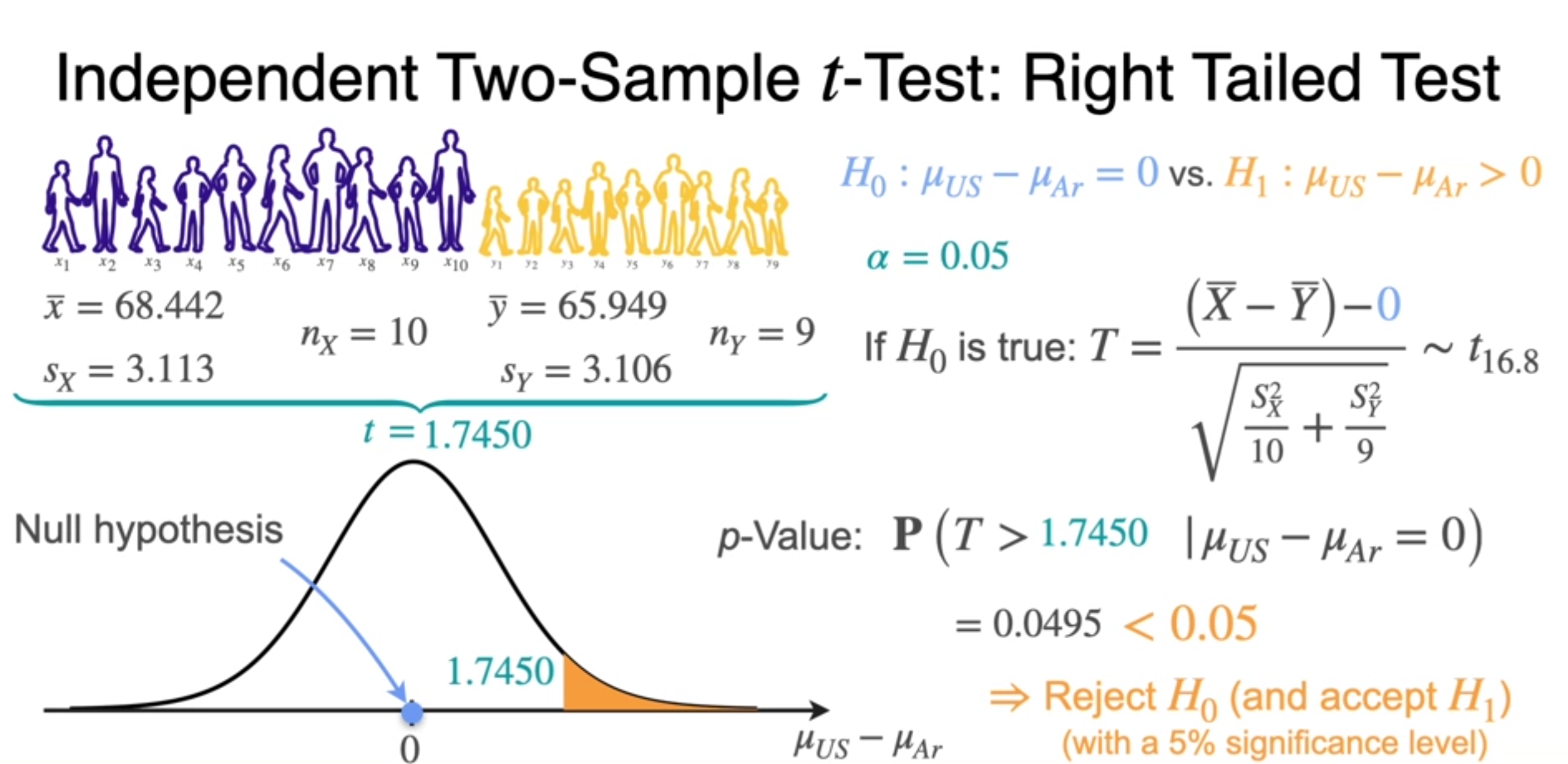
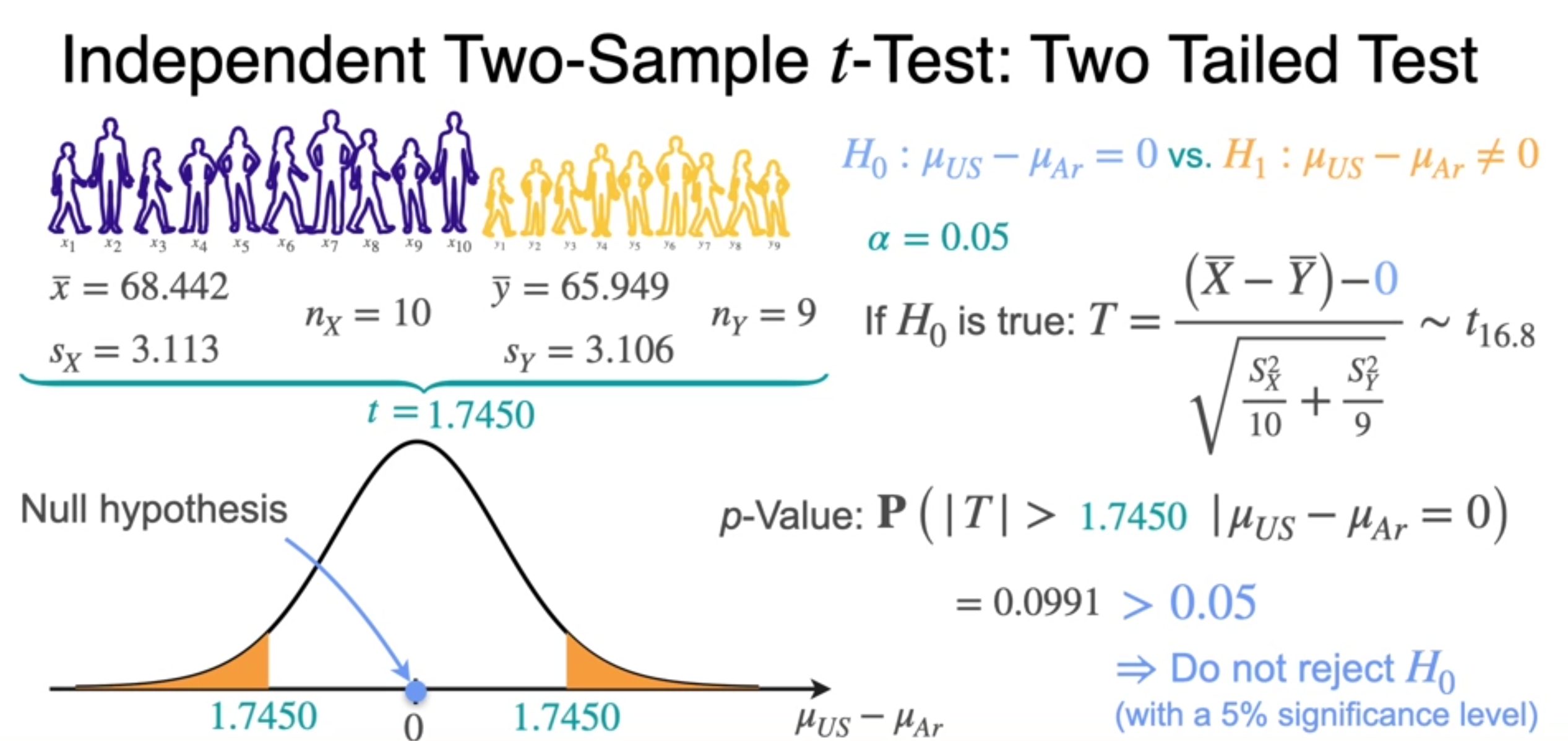
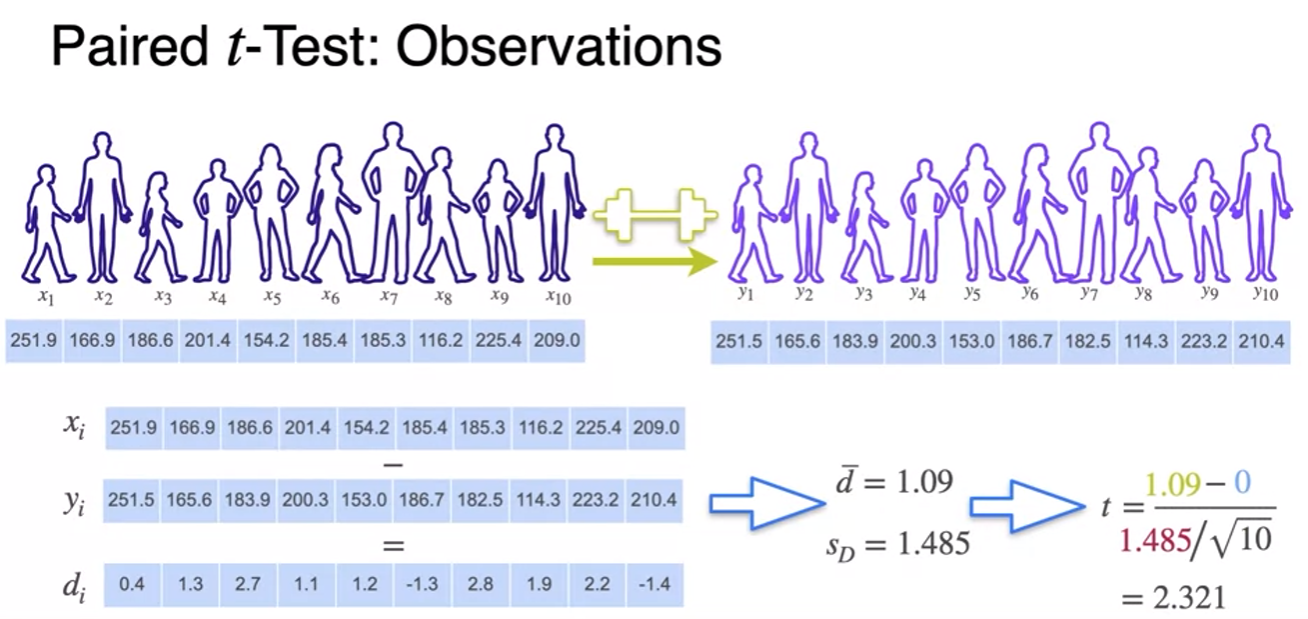
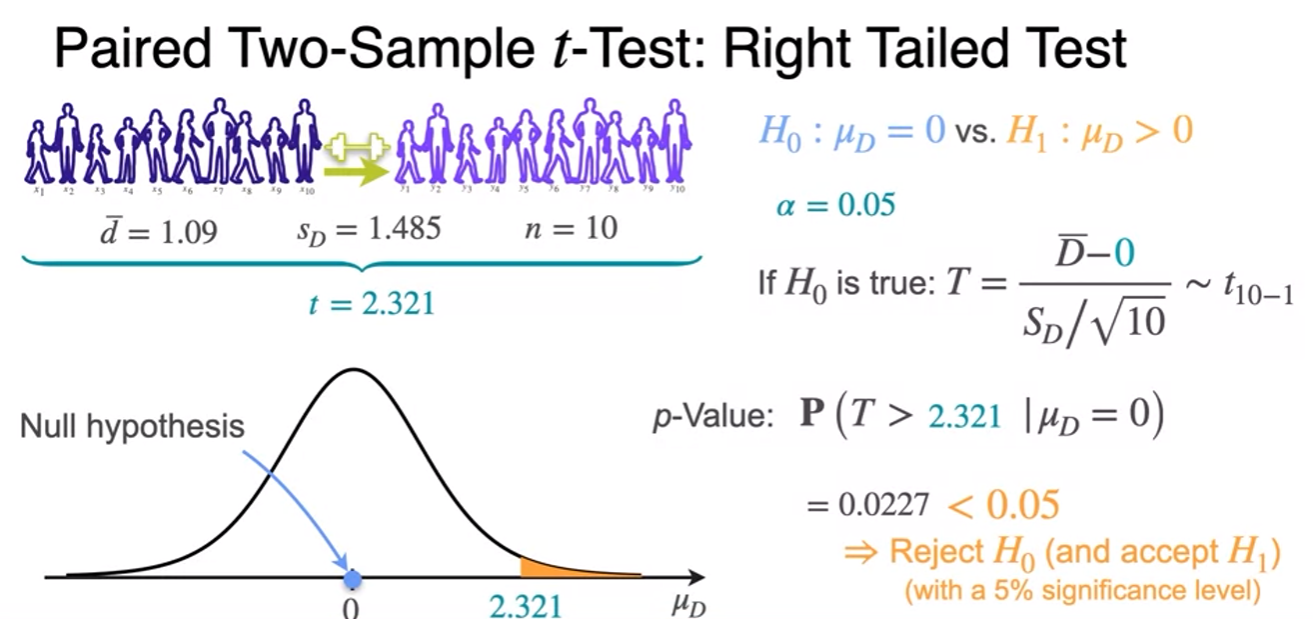
Paired t-Test

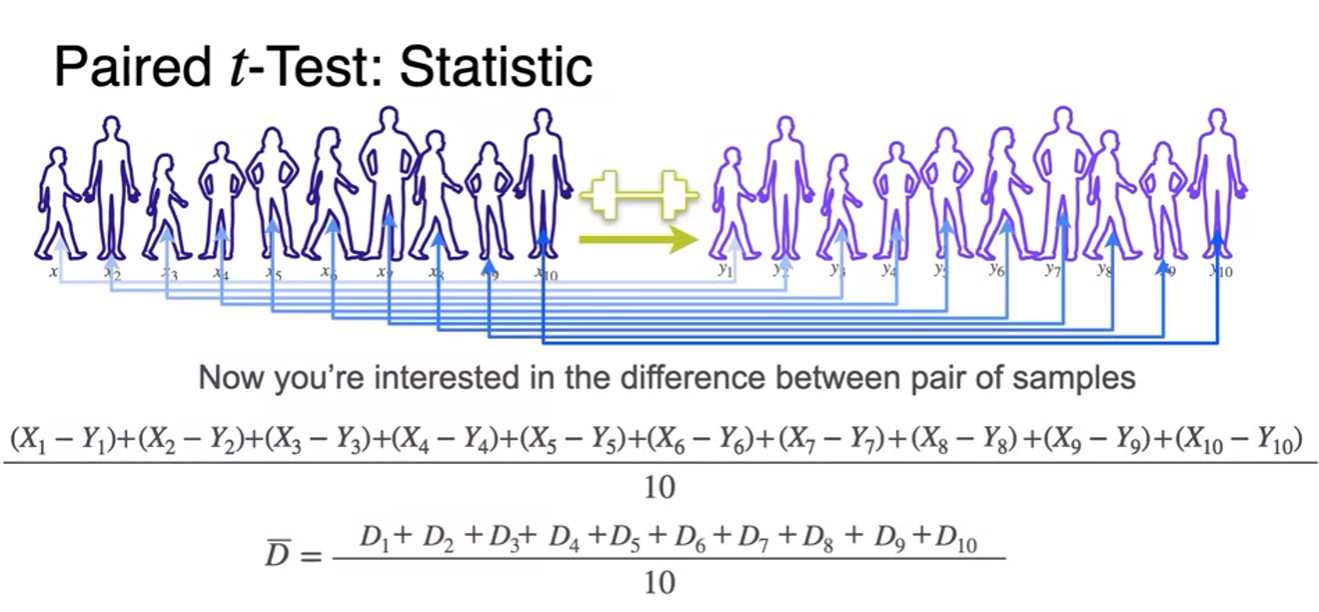
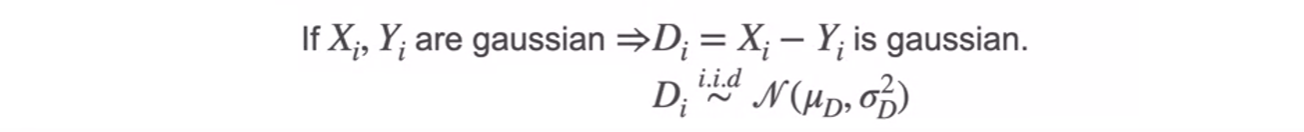
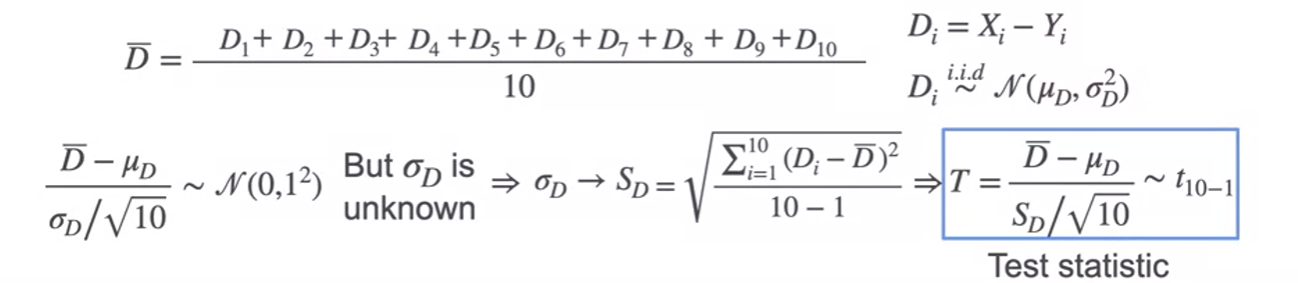
• replace population standard deviation(unknown) by the sample standard deviation

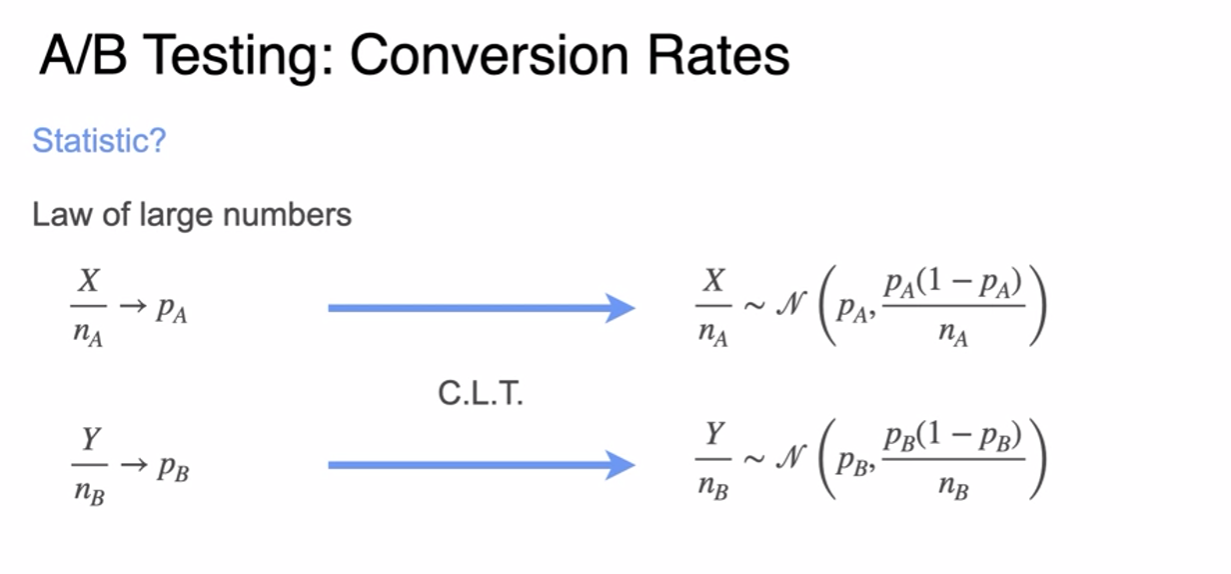
ML Application: A/B Testing

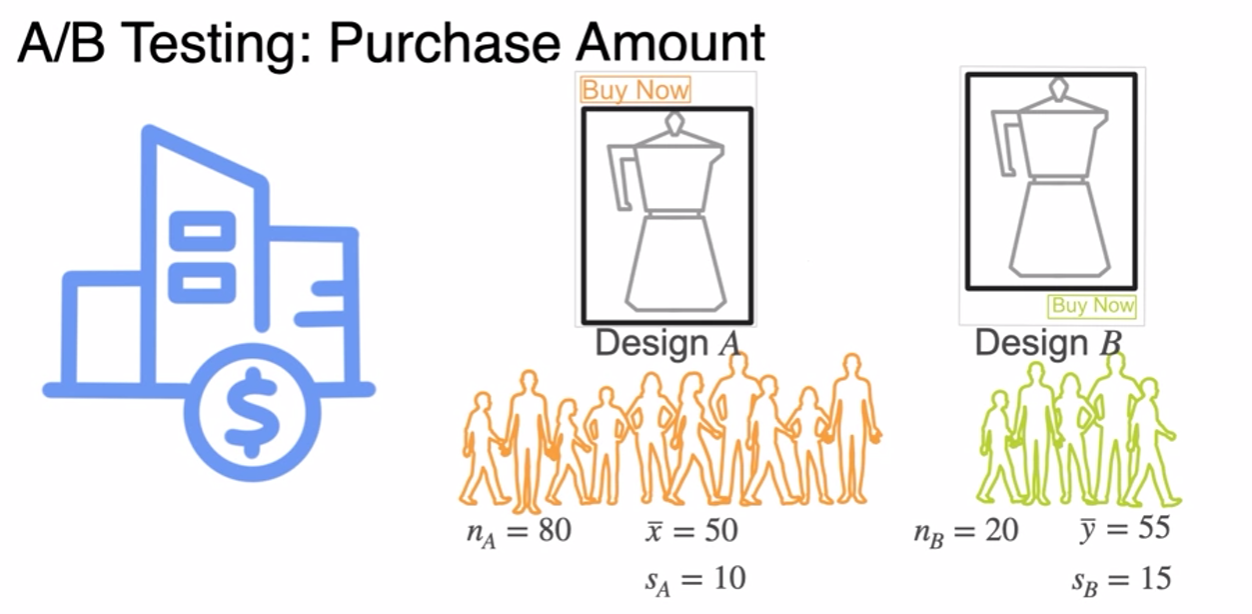
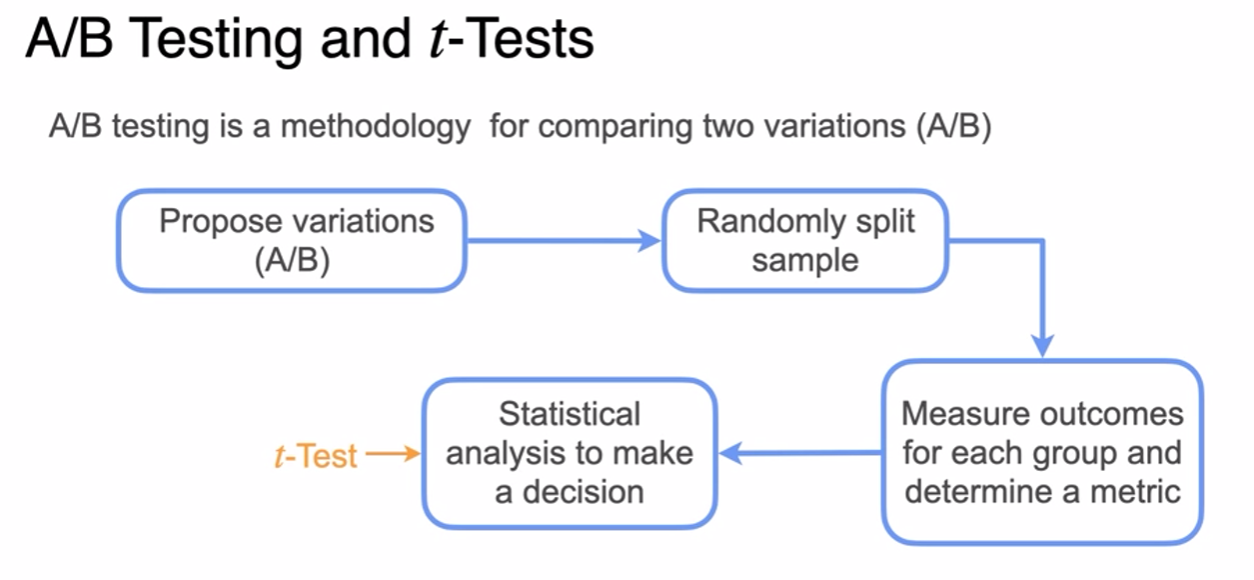
• is B better?