Sampling and Point examination - Week 3

Lesson 1 - Population and Sample

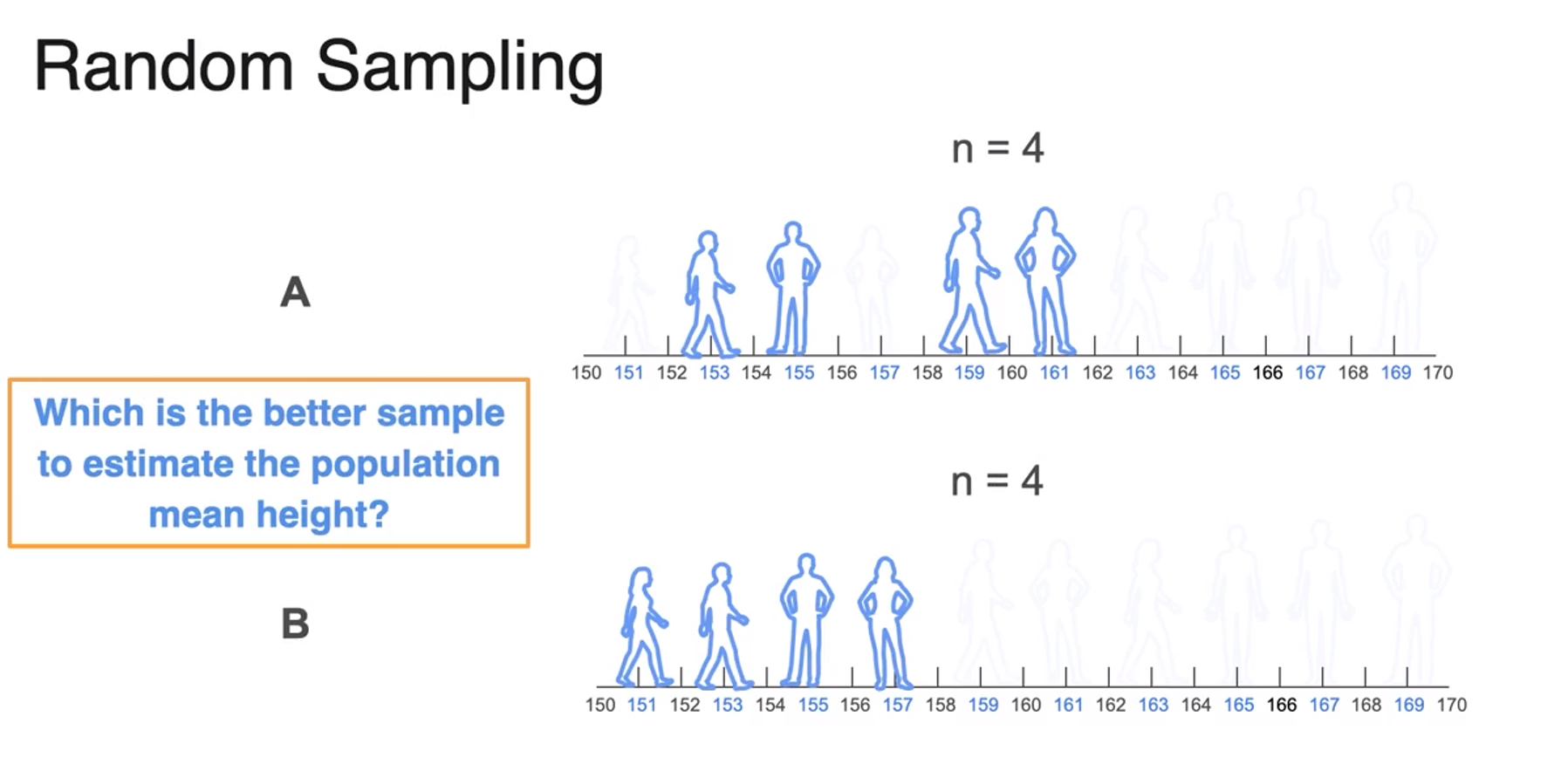
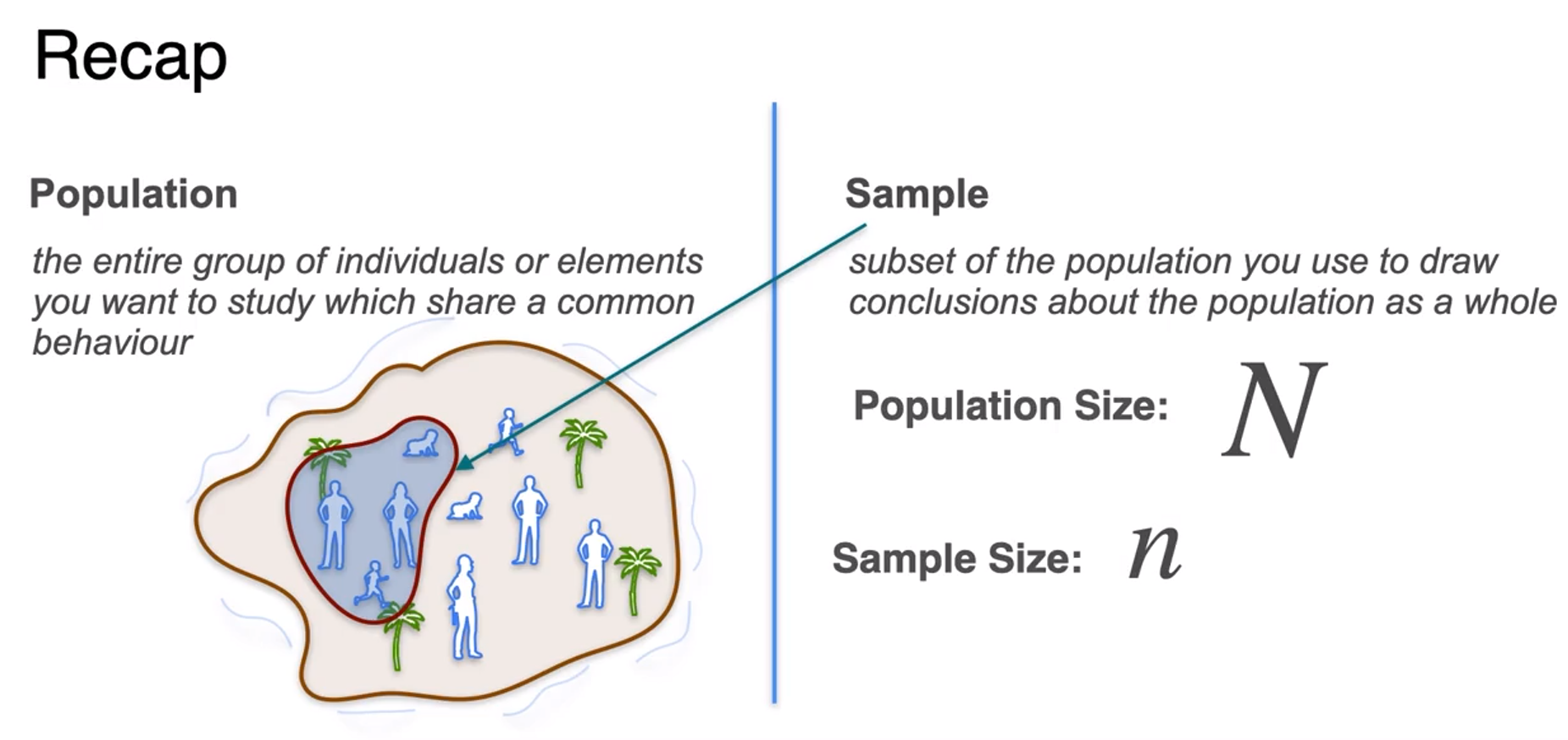
Population and Sample

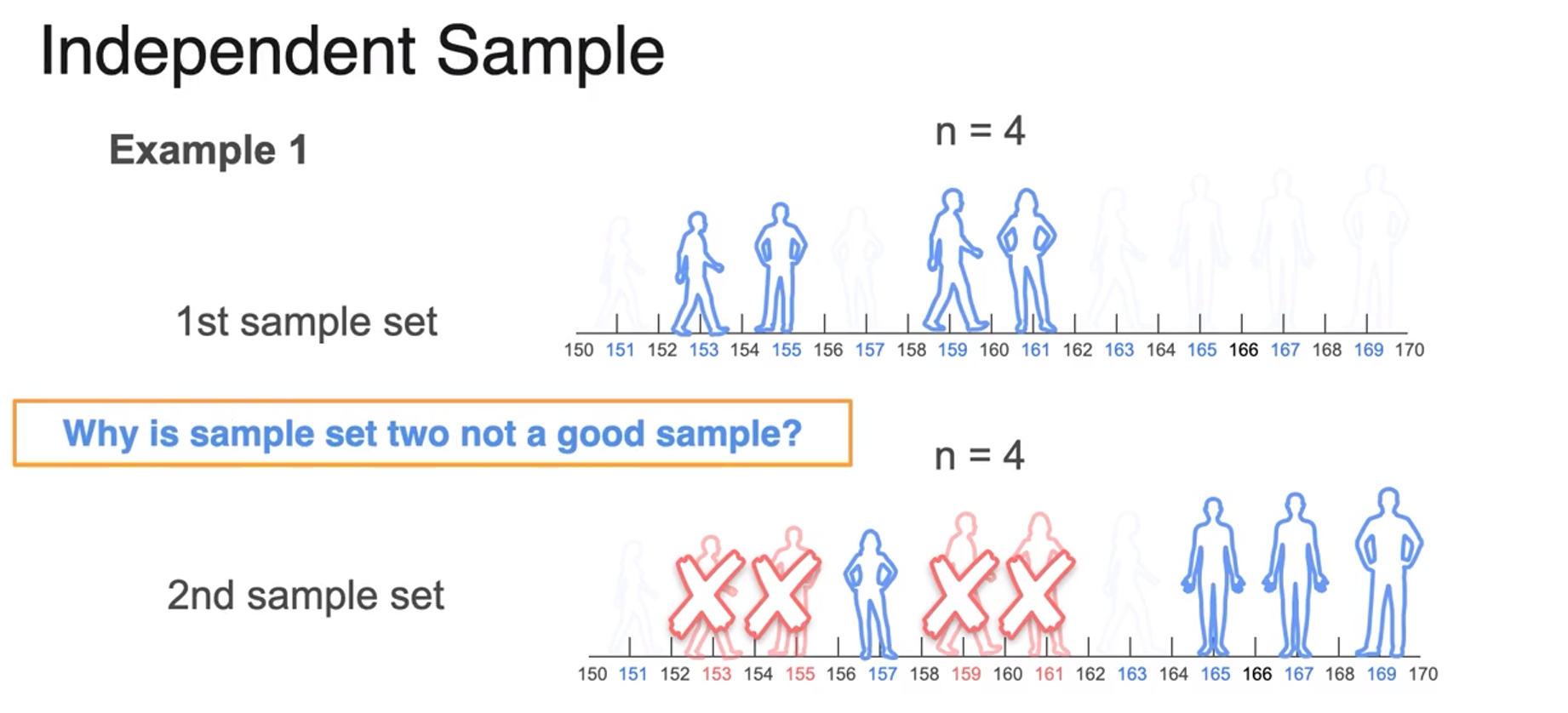
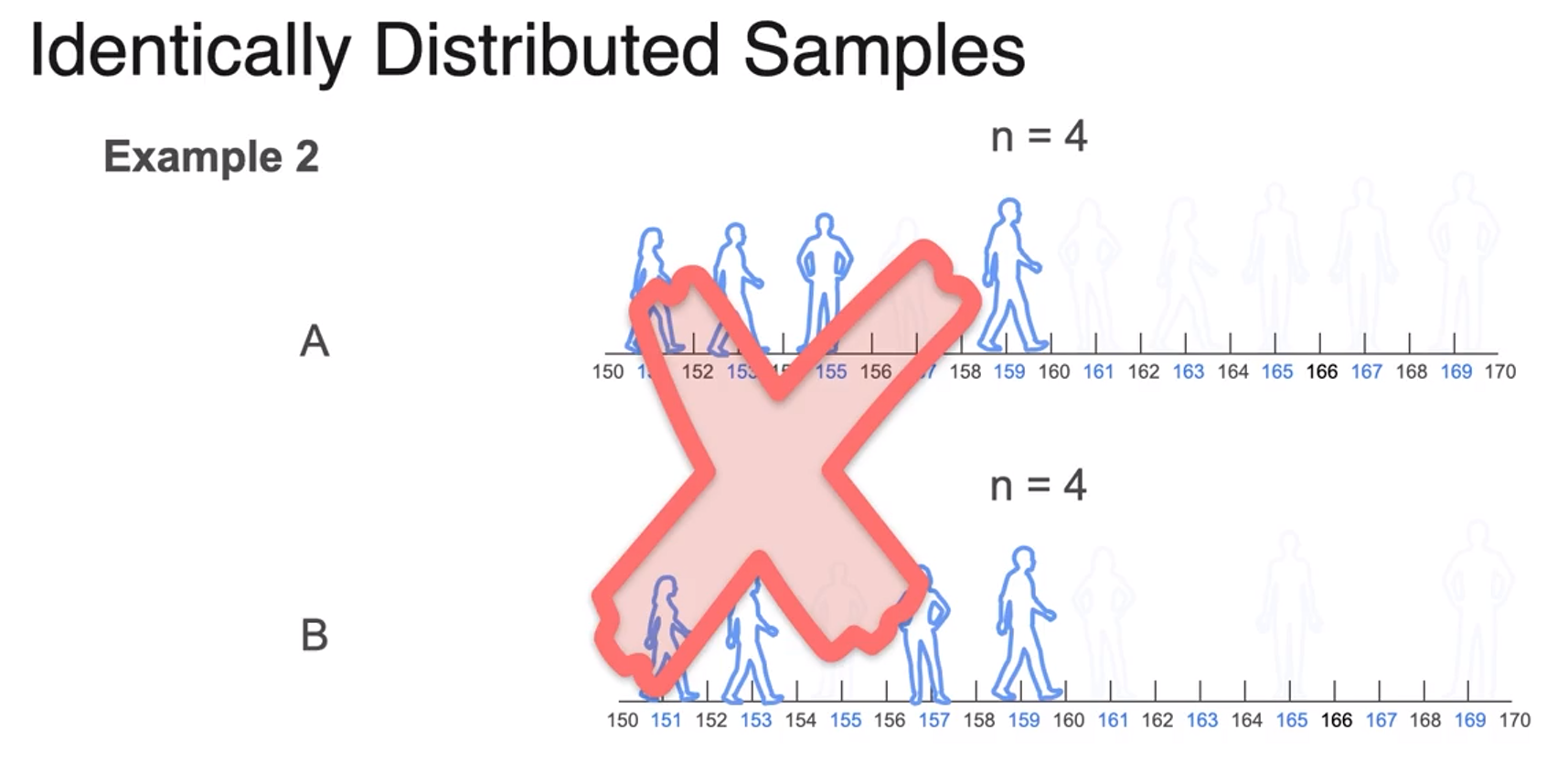
• this is bad sample because it depends on 1st sample.

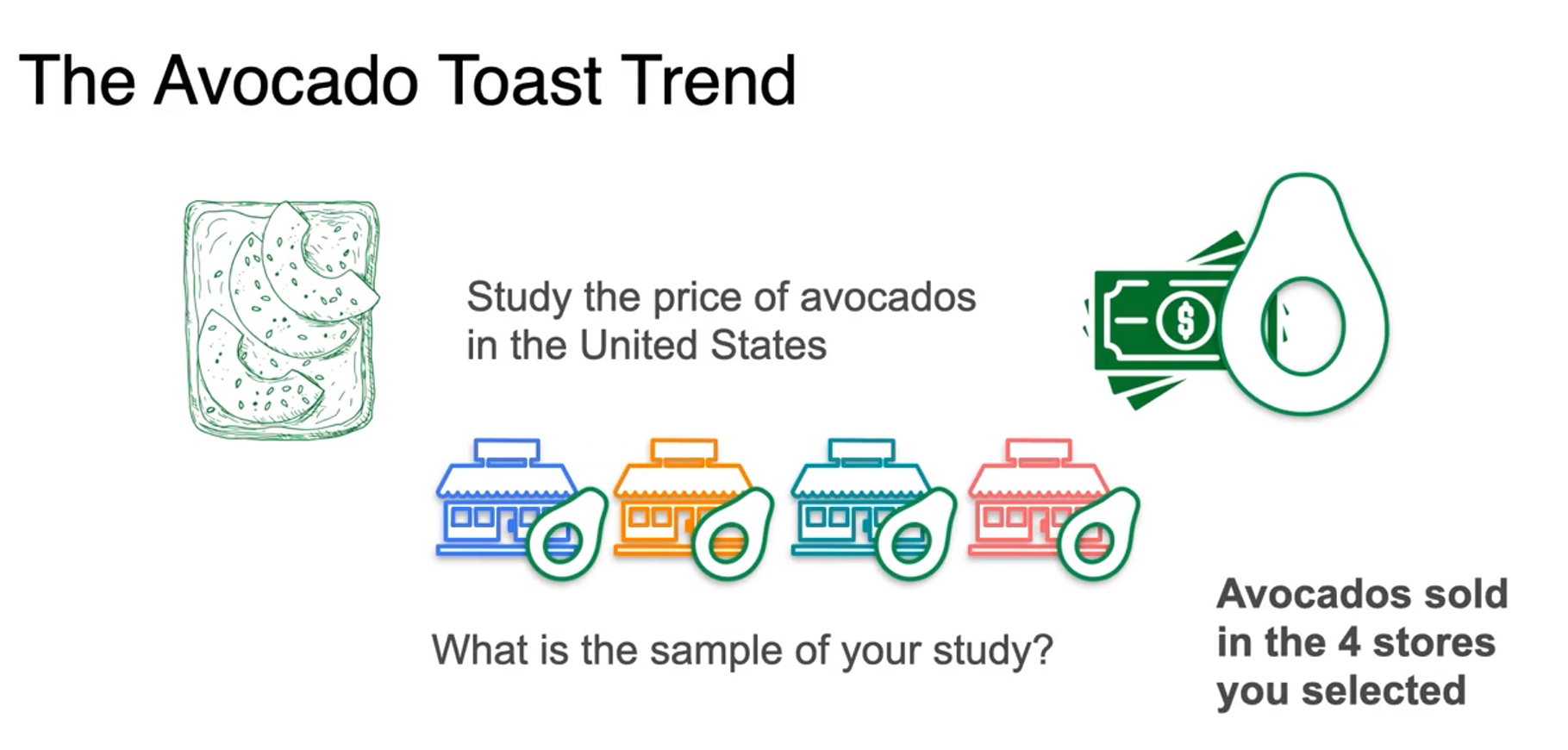
• population is sold avocados in us

• sample is sold avocados in 4 stores

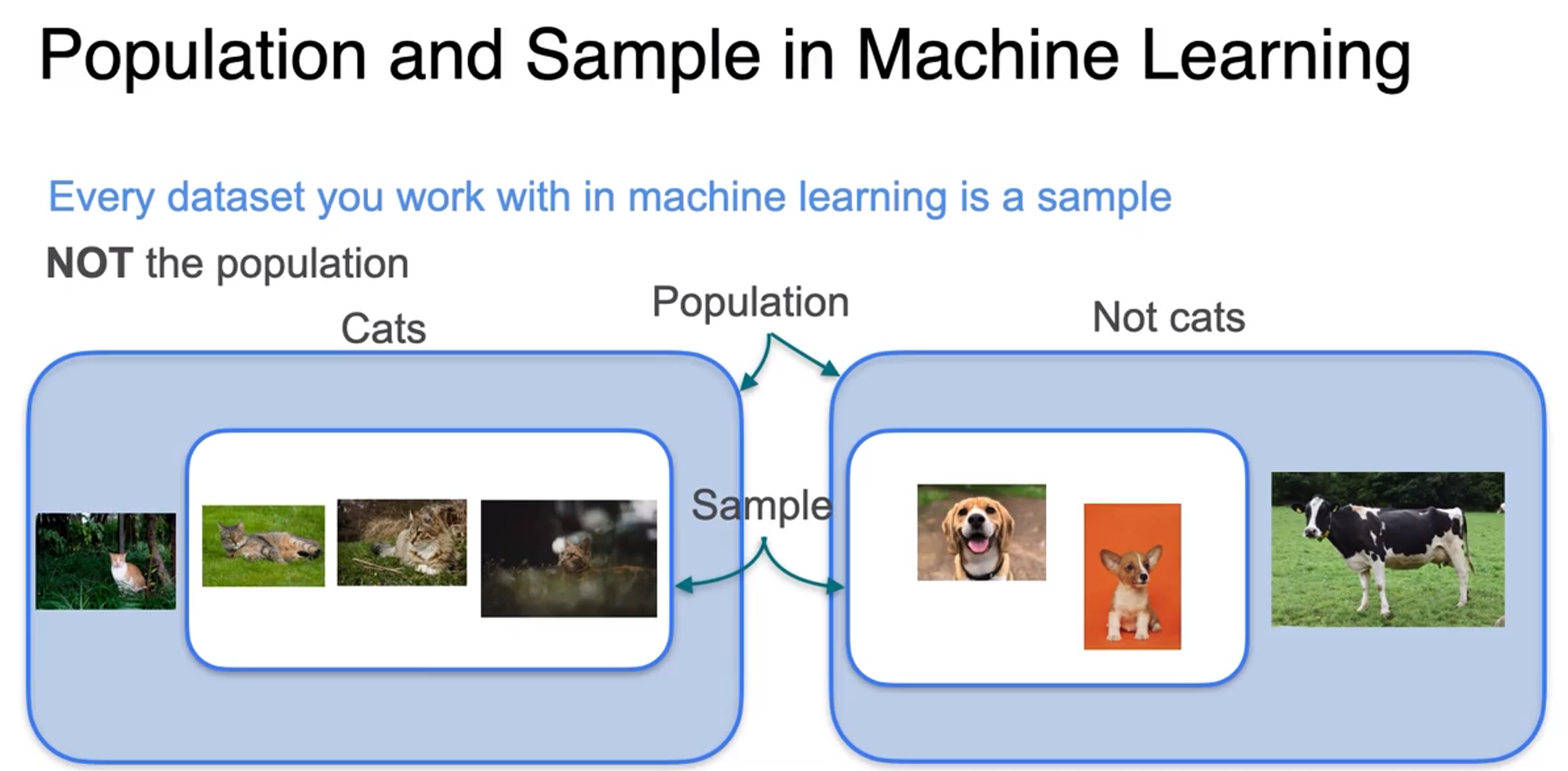
• In ML every dataset you work it is sample no matter how big the dataset is.

Sample Mean

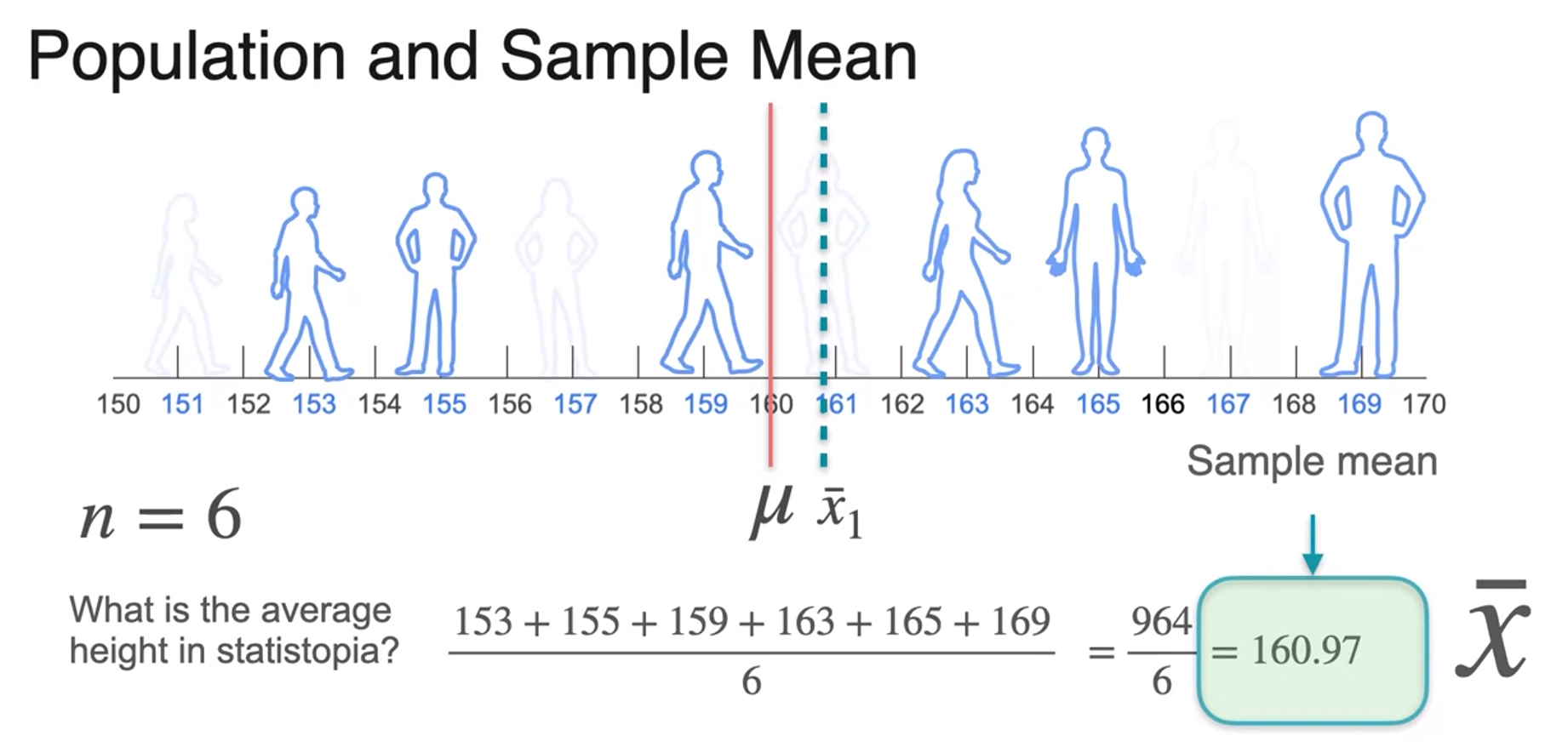
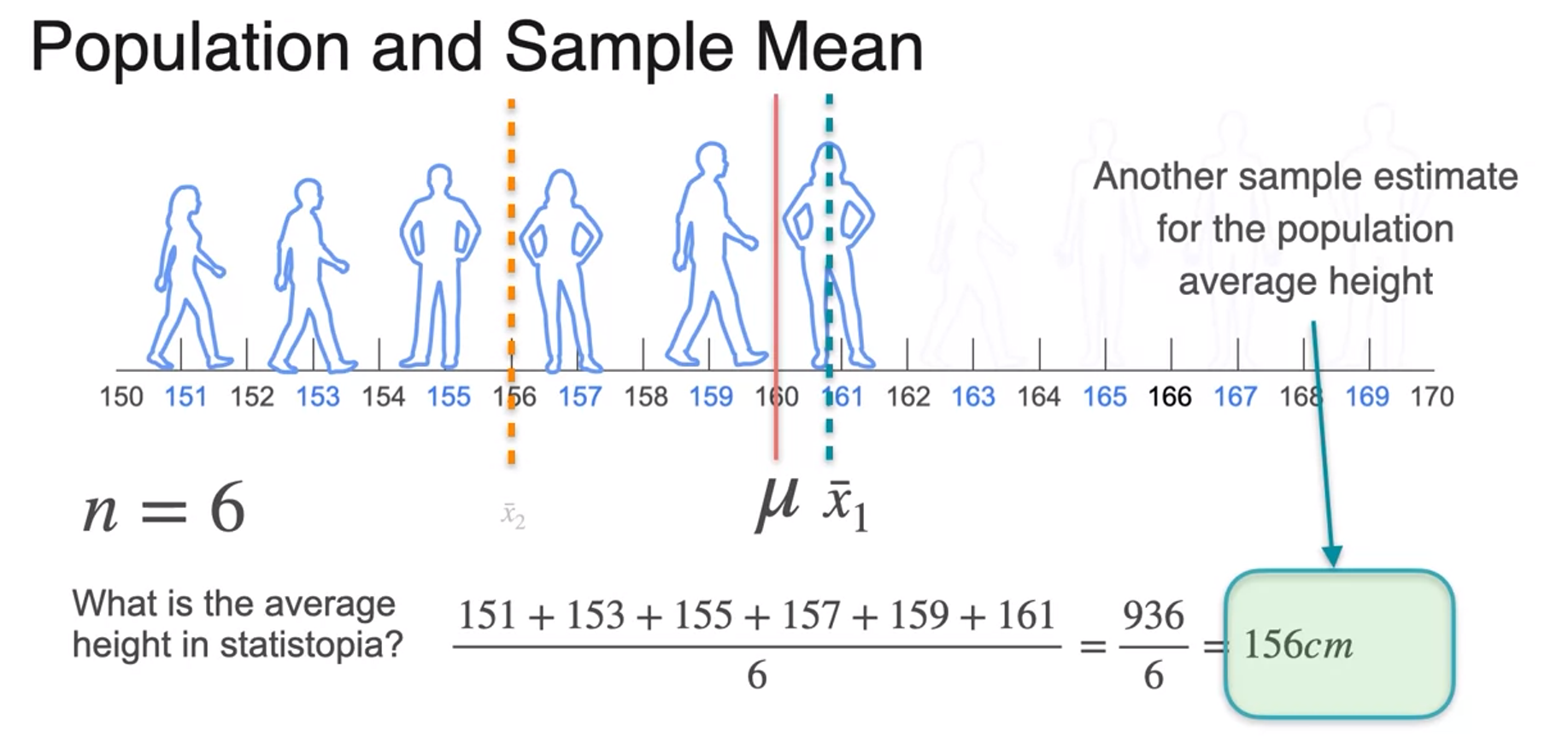
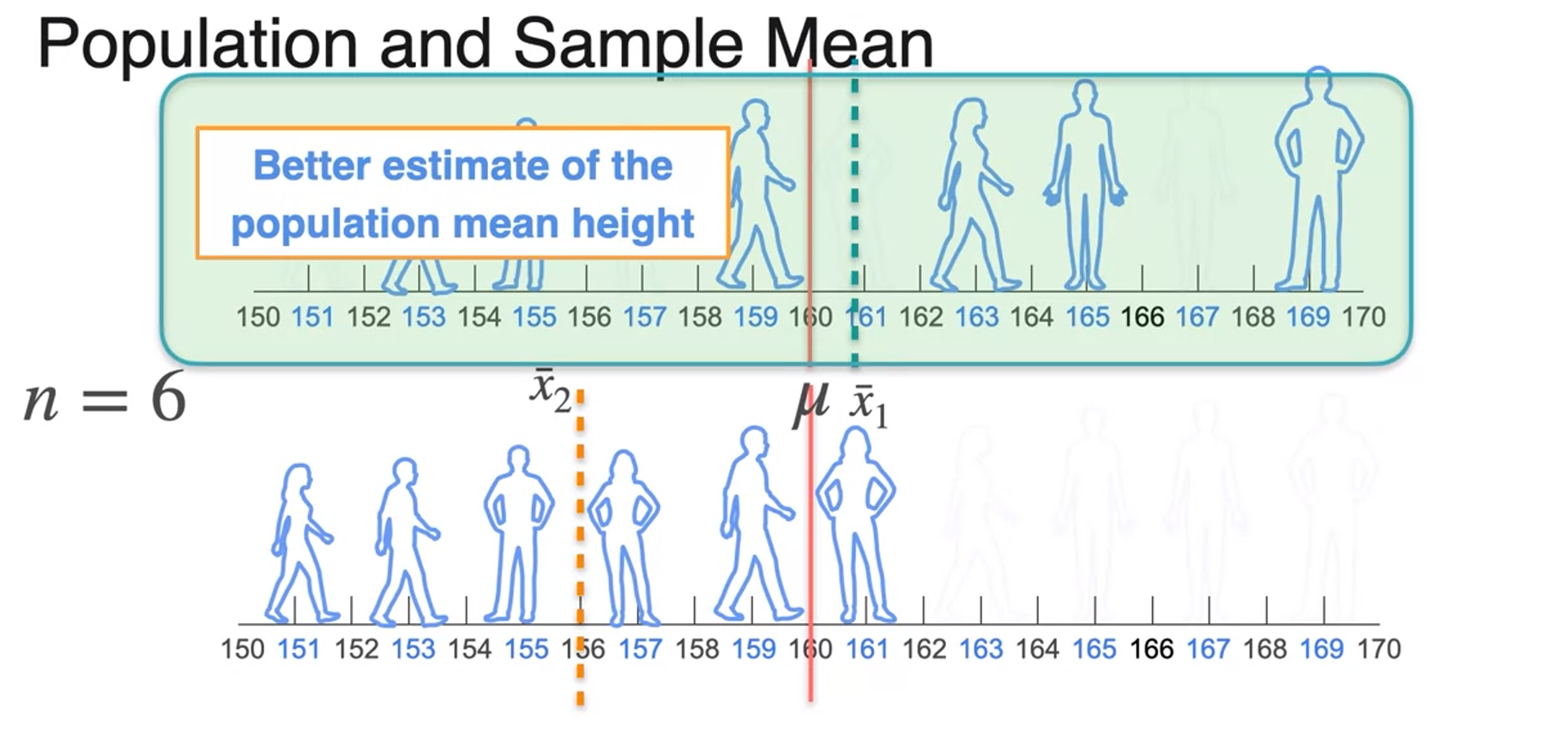
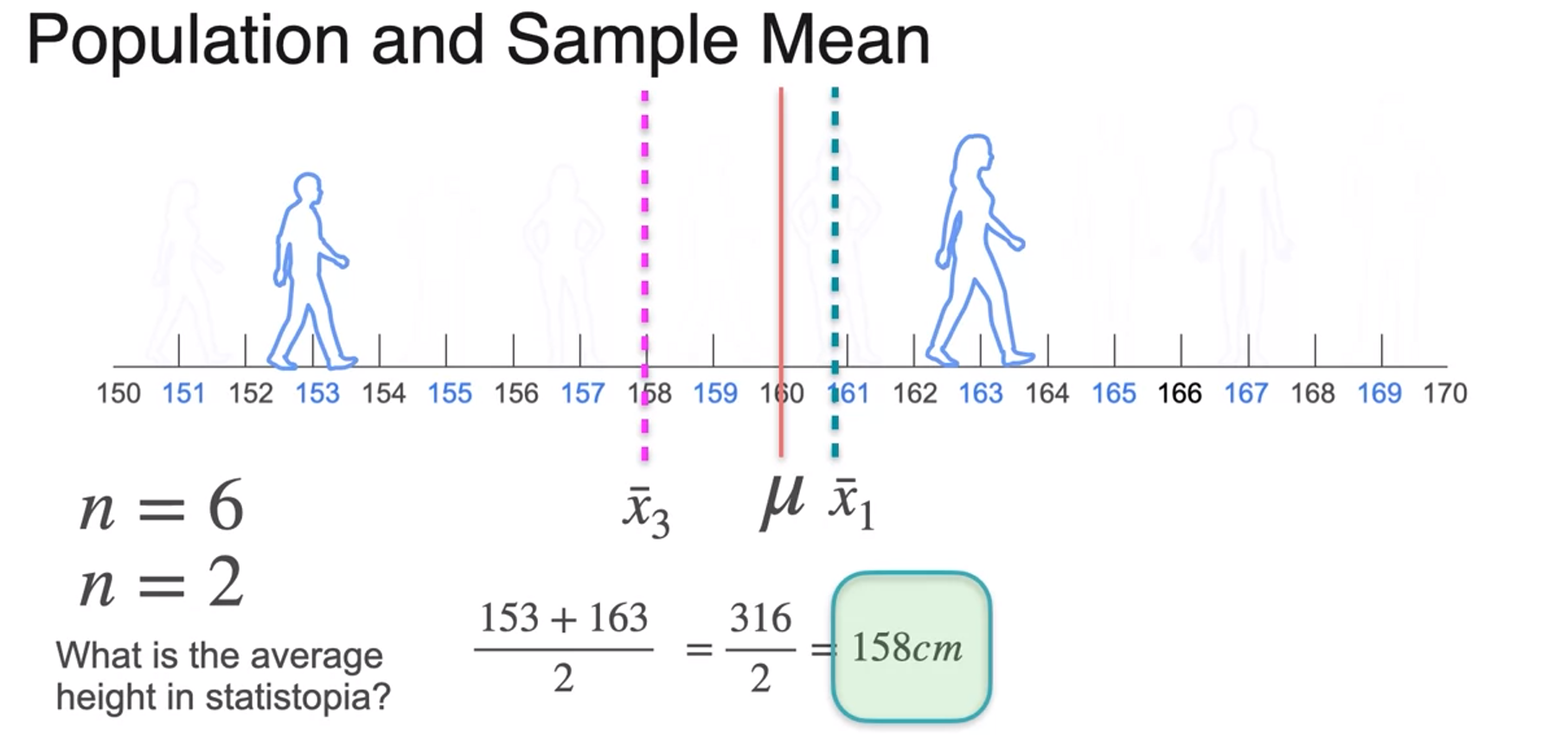
• The bigger sample size the better the estimate you're going to get

Sample Proportion

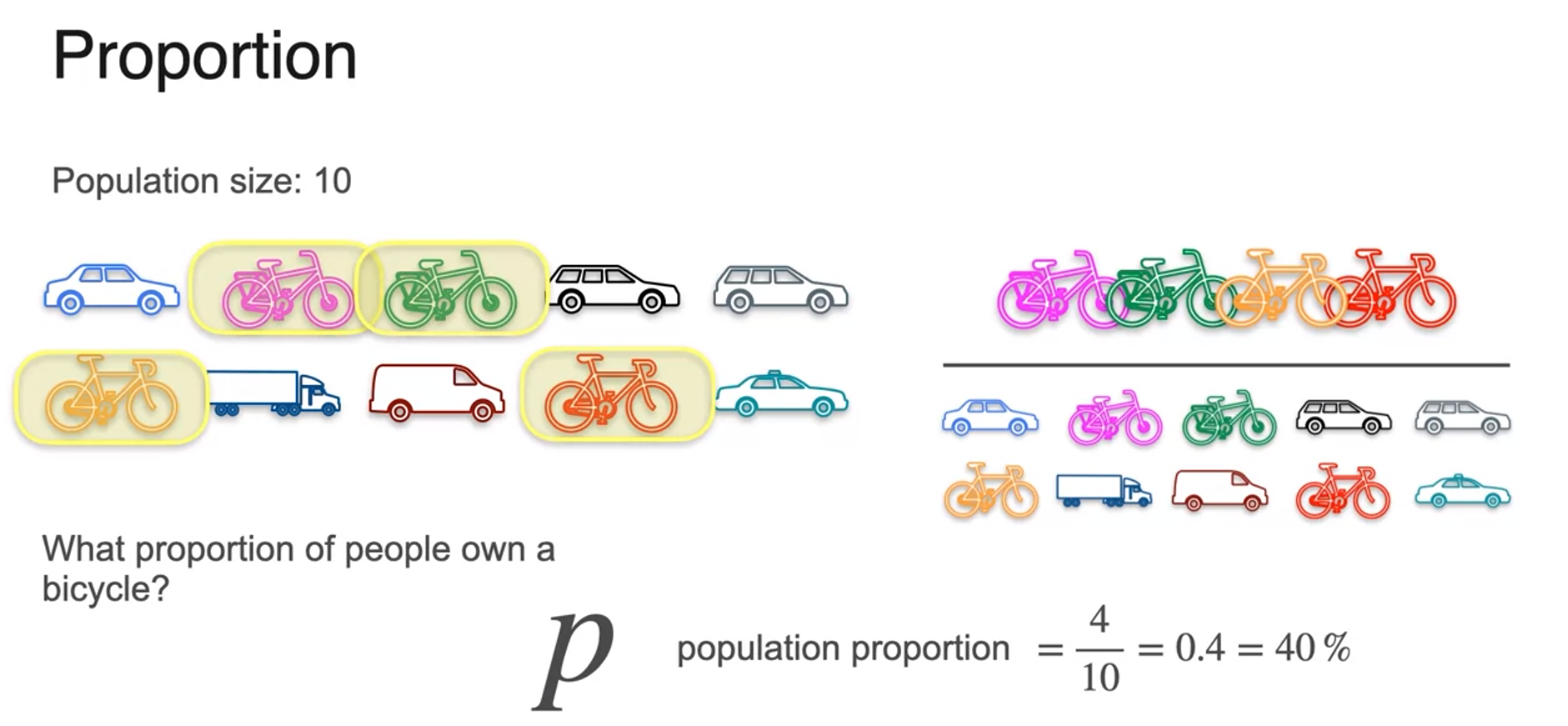
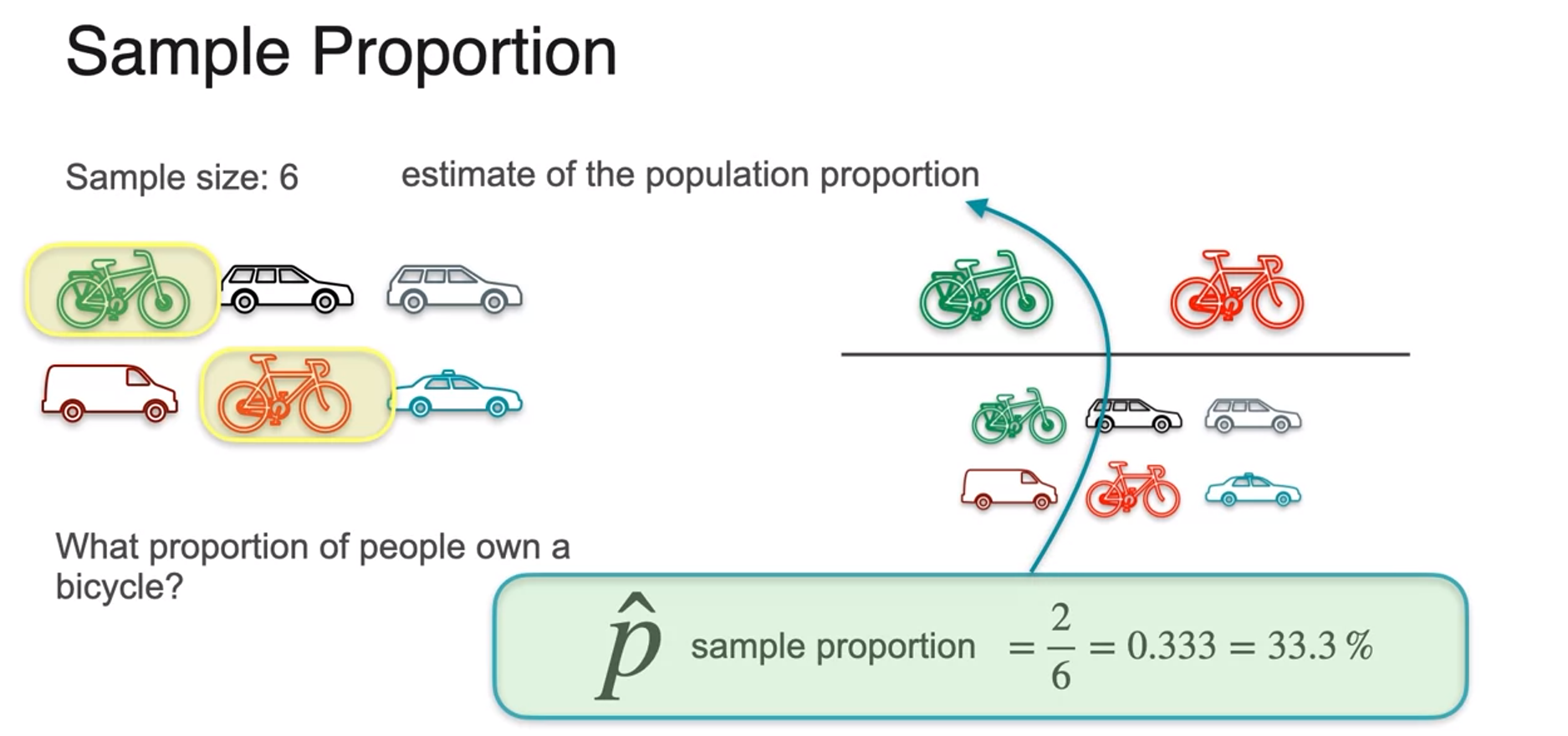
• if you don't have access to the population size?
  • using randomly sample data

Sample Variance

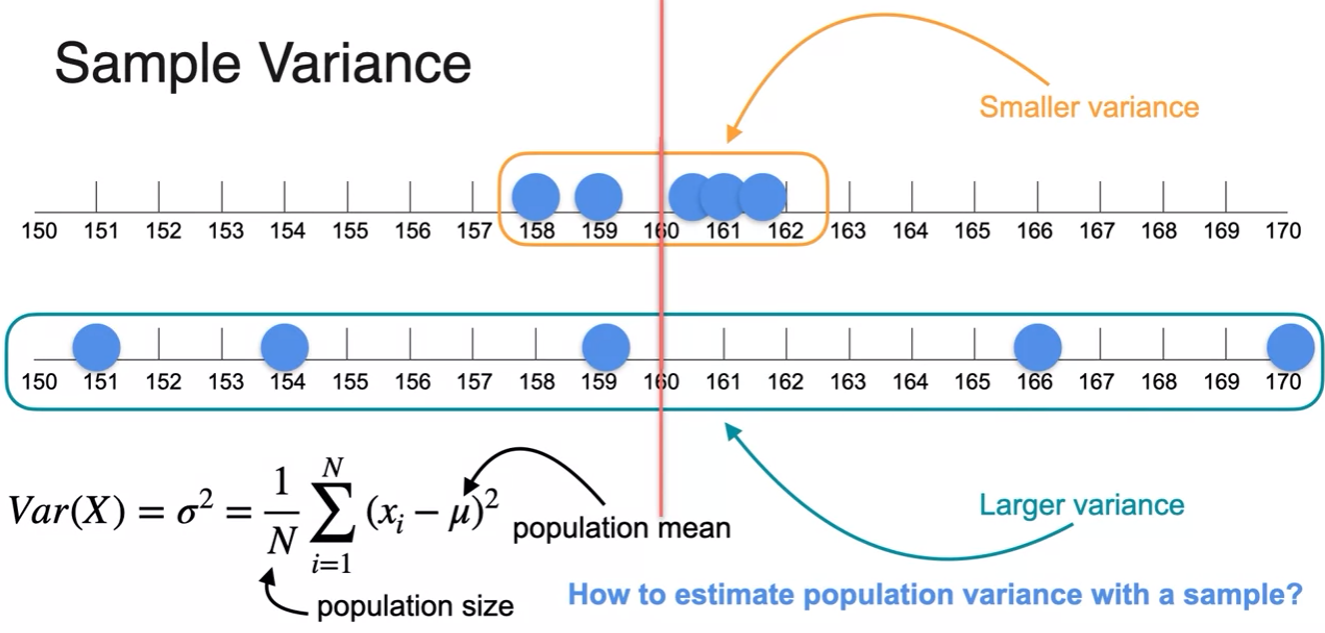
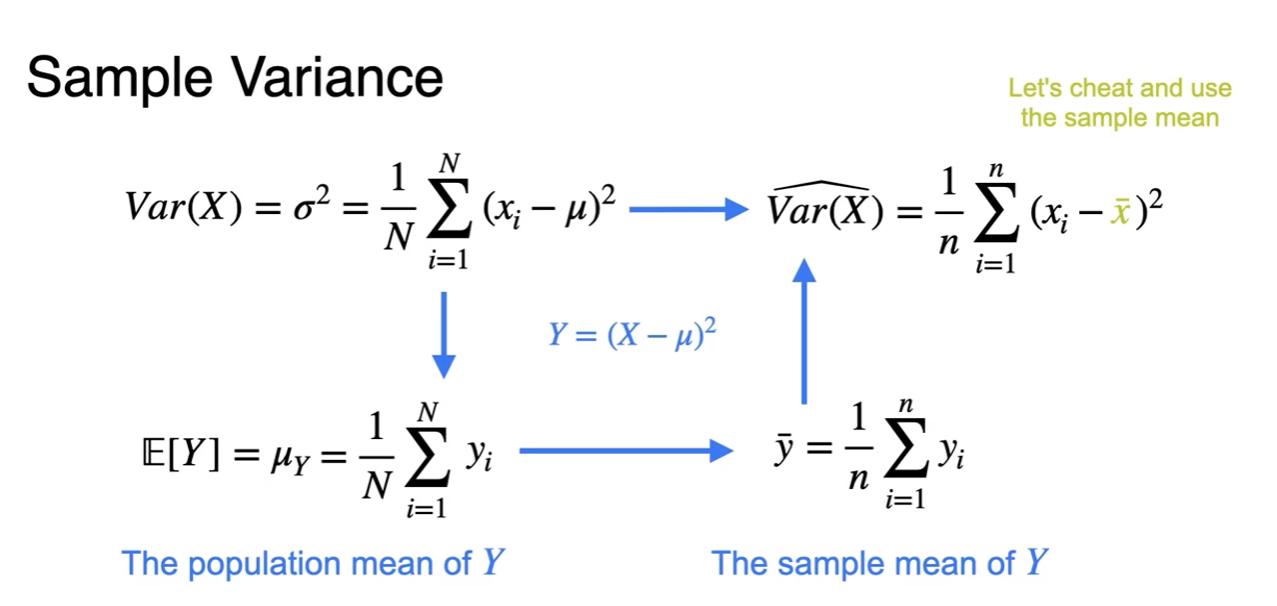
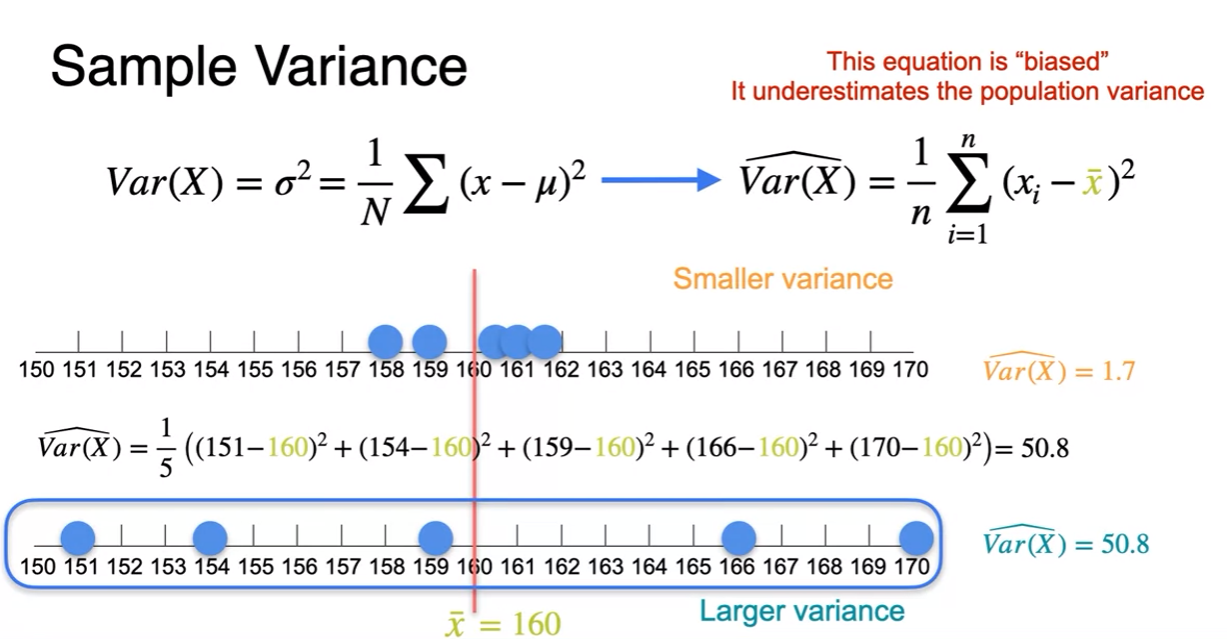
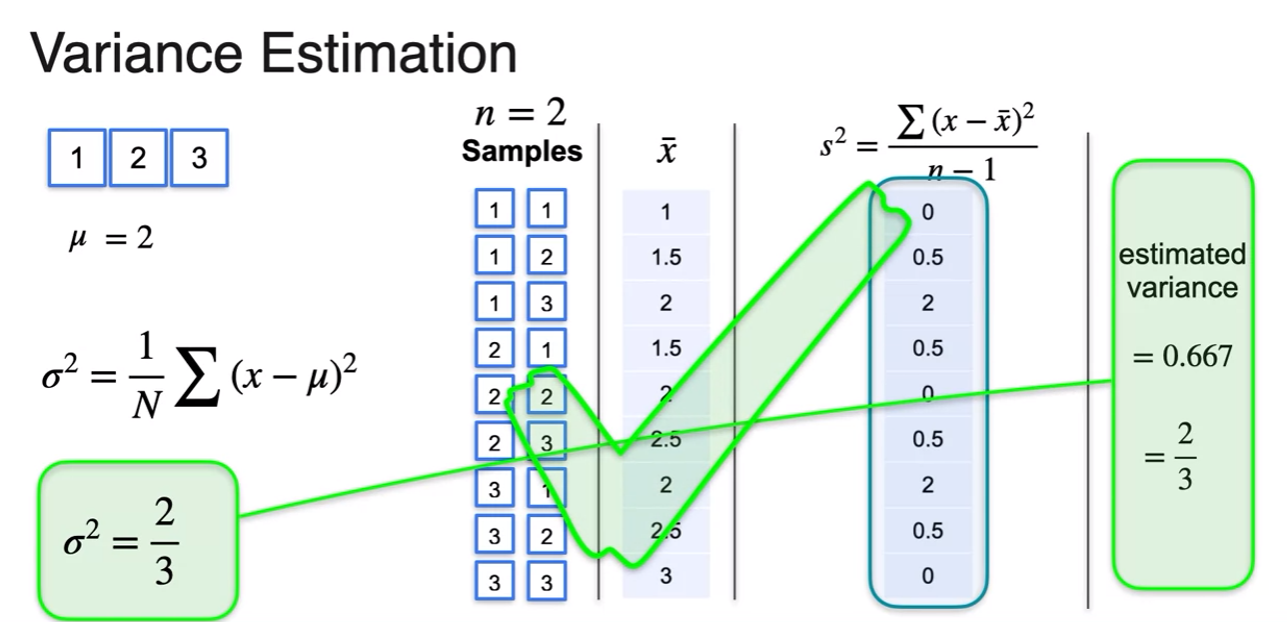
• so using only given sample various as below
  $s^2 = \frac{\Sigma(x-\overline{x})^2}{n-1}$

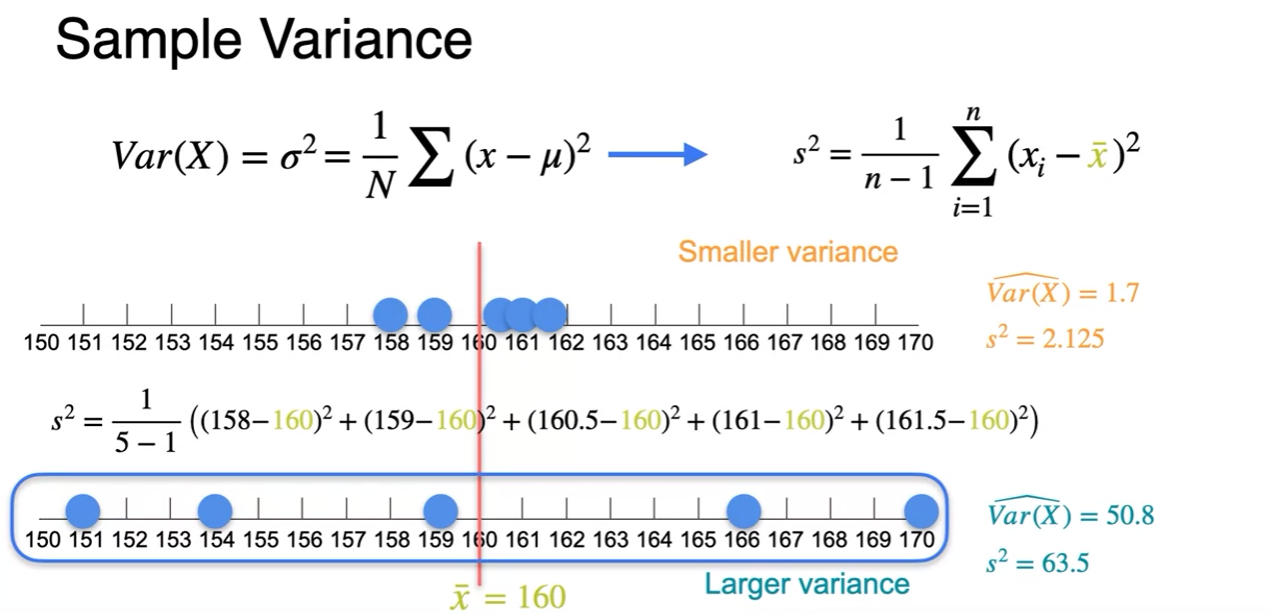
• estimated increased slightly

• For sample variance formula sample when unkown population mean, use sample mean $\overline{x}$

Law of Large Numbers

• there is always scale issue

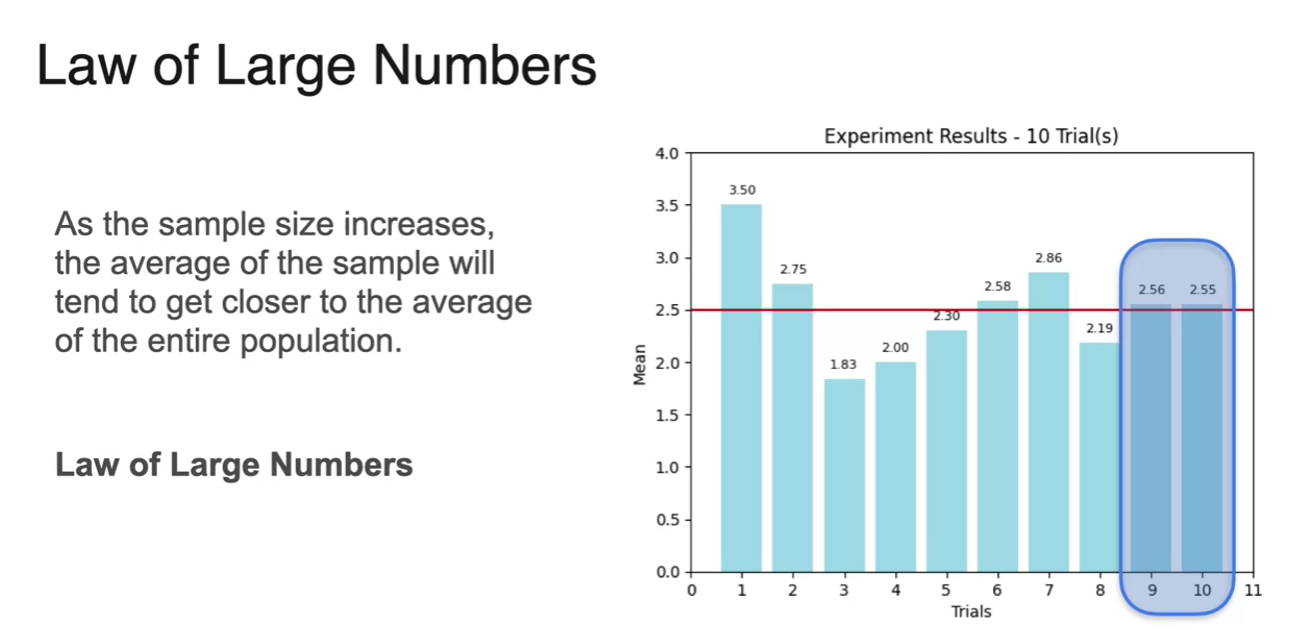
• Law of large numbers happen under this condition

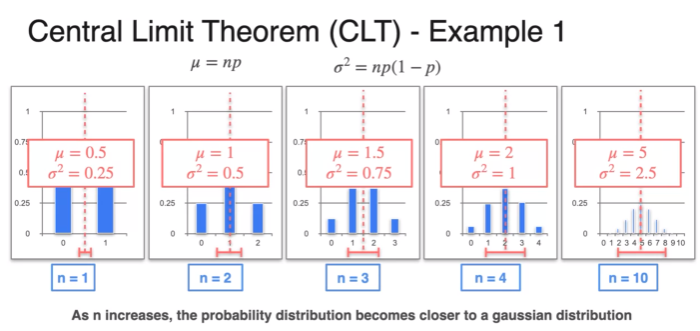
Central Limit Theorem - Discrete Random Variable

• as you increase number of variables become more look like gaussian distribution

Central Limit Theorem - Continuous Random Variable

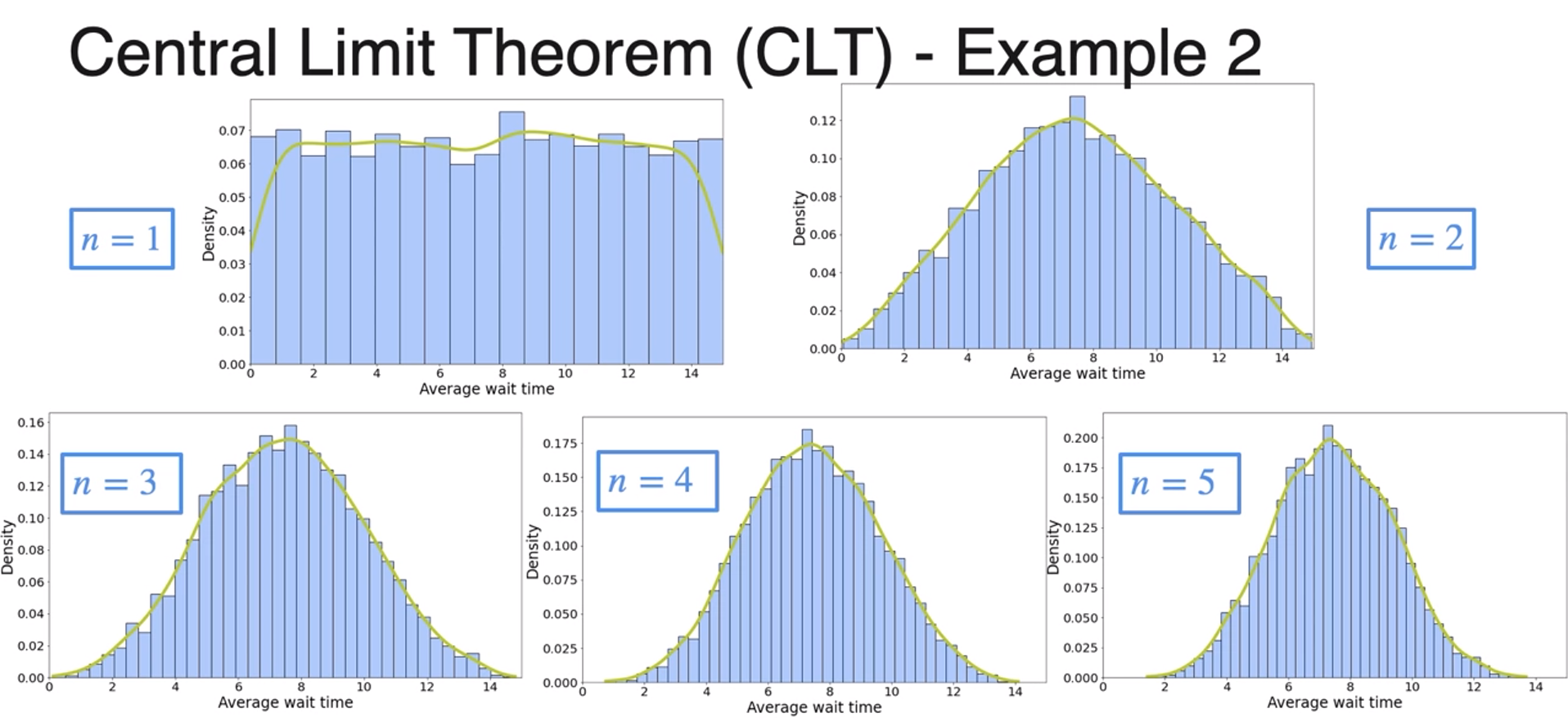
• getting more symmetrical around 7.5

• with n grows so does the variance of the average

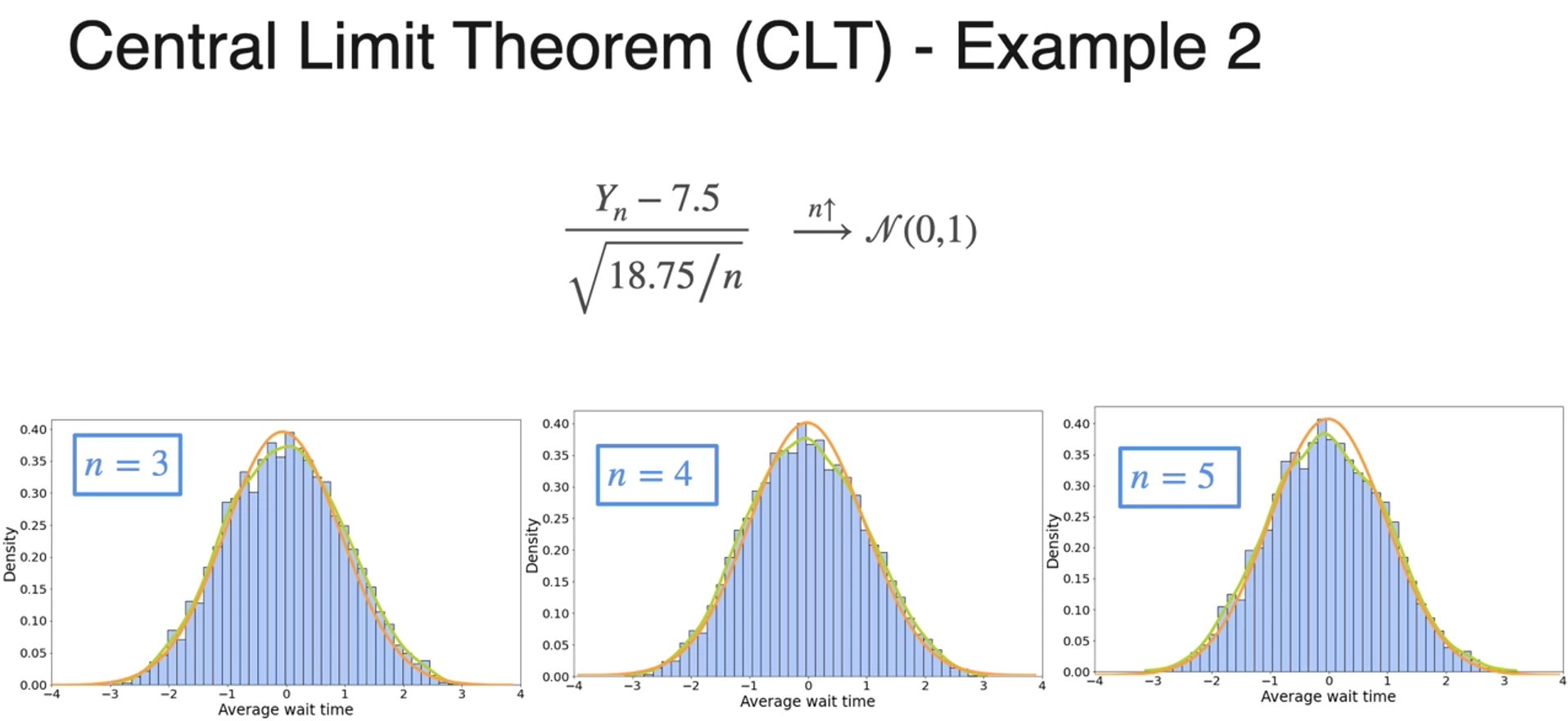
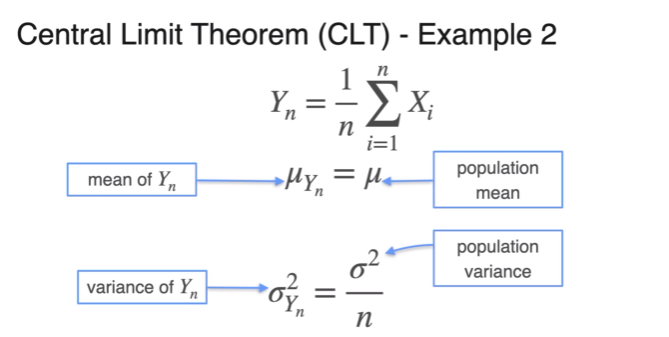
• mean stays and variance get smaller

• in practice this is true around 30 or higher

Lesson 2 - Point Estimation

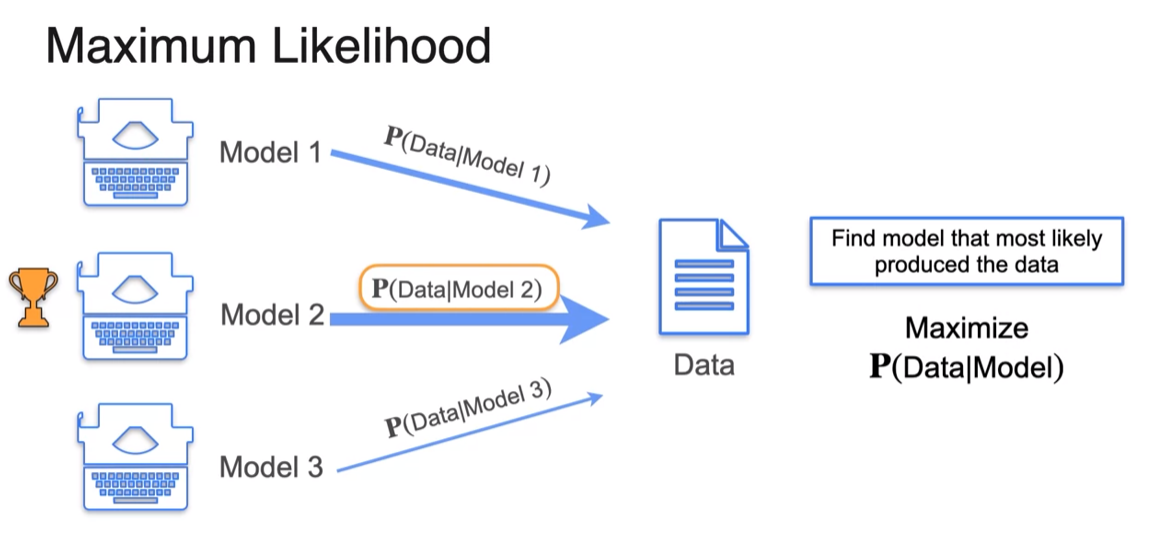
Point Estimation

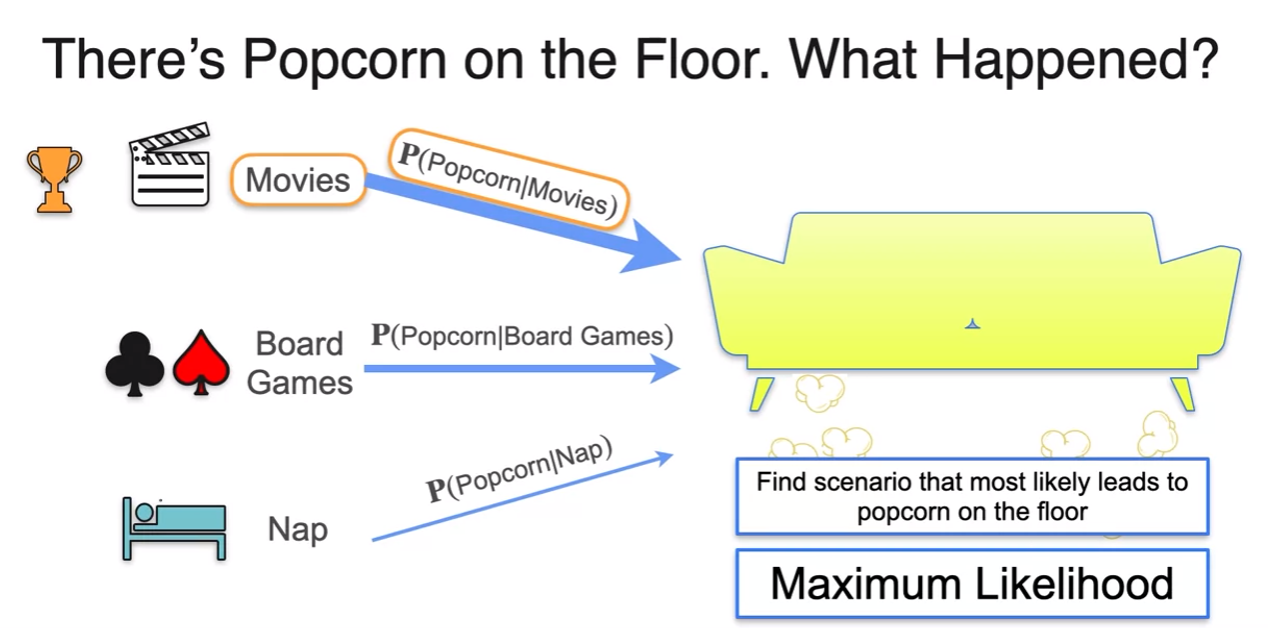
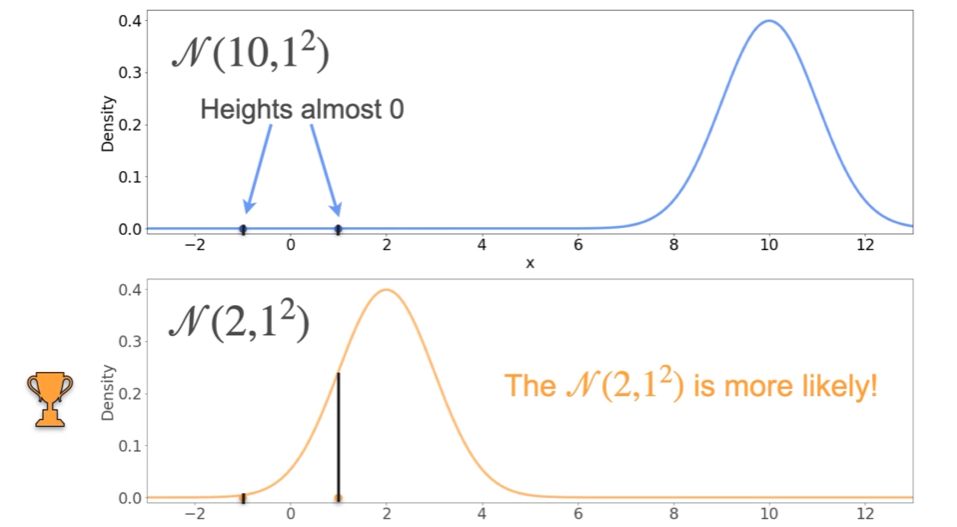
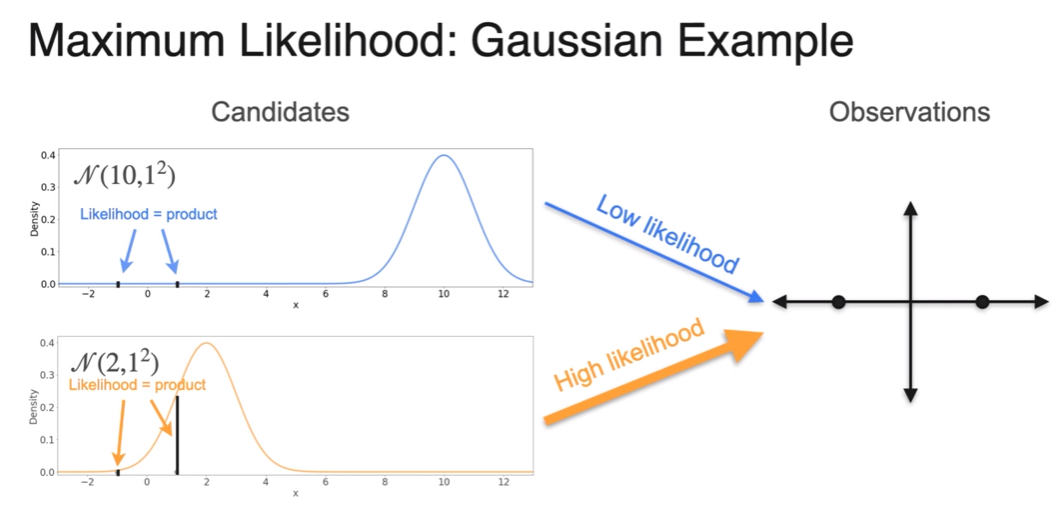
• we picked the scenario that made the evidence more likely

MLE: Bernoulli Example

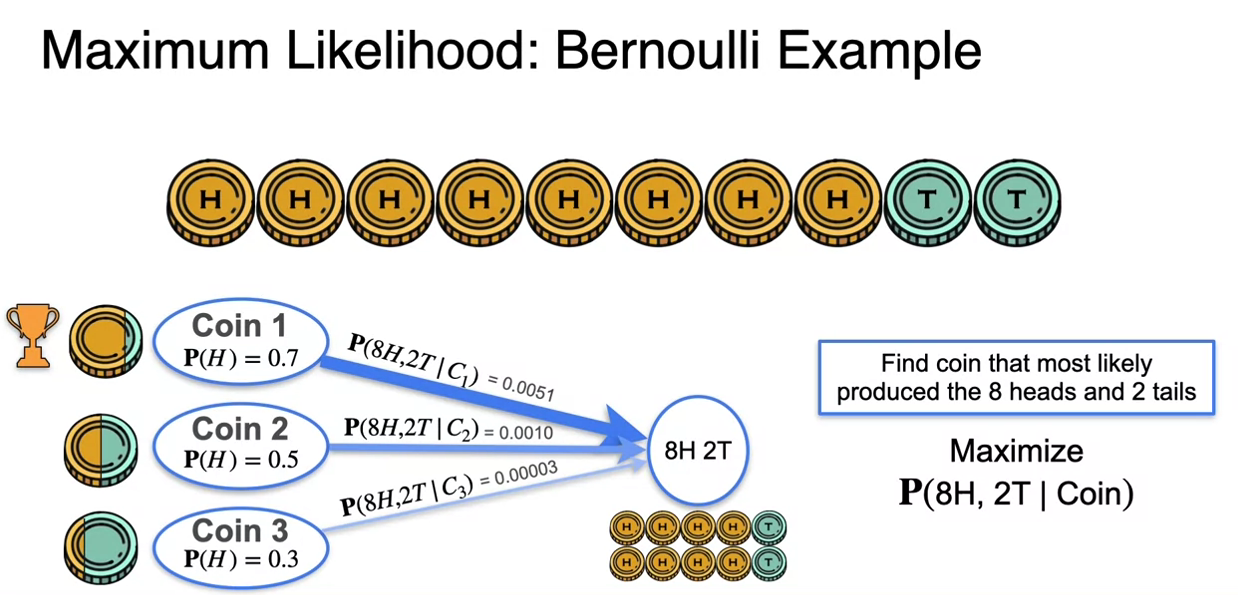
• so the best possible coin we would have generated this flips is a coin probability of heads is 8 over 10.

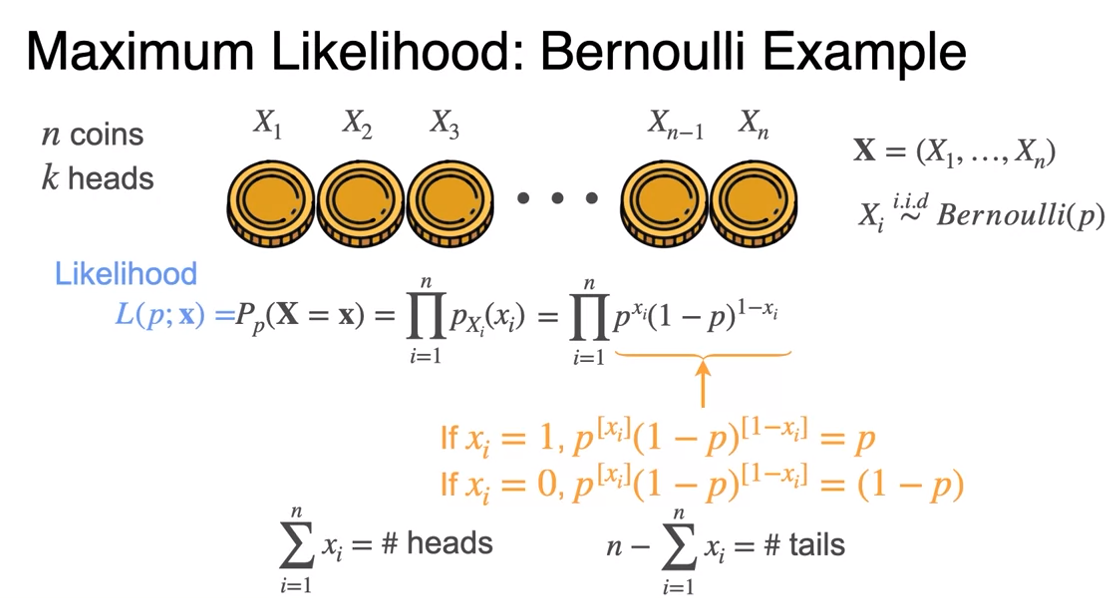
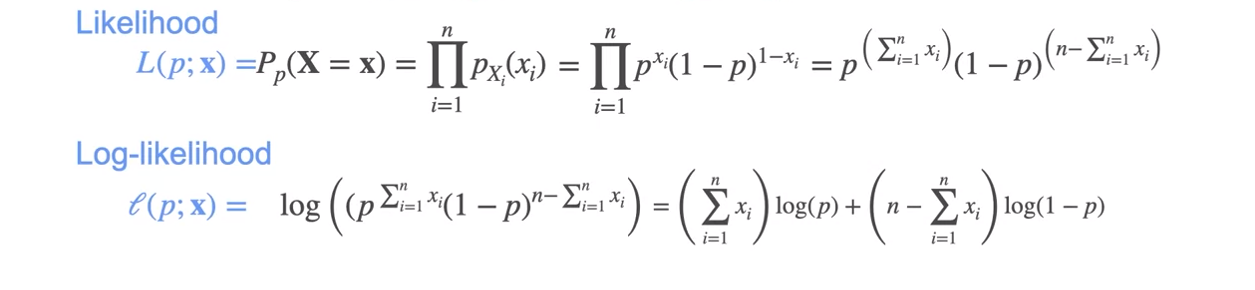
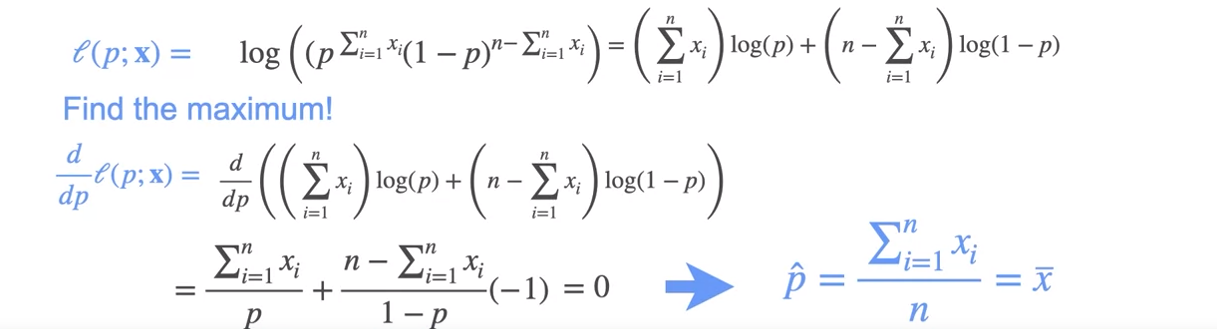
MLE: Gaussian Example

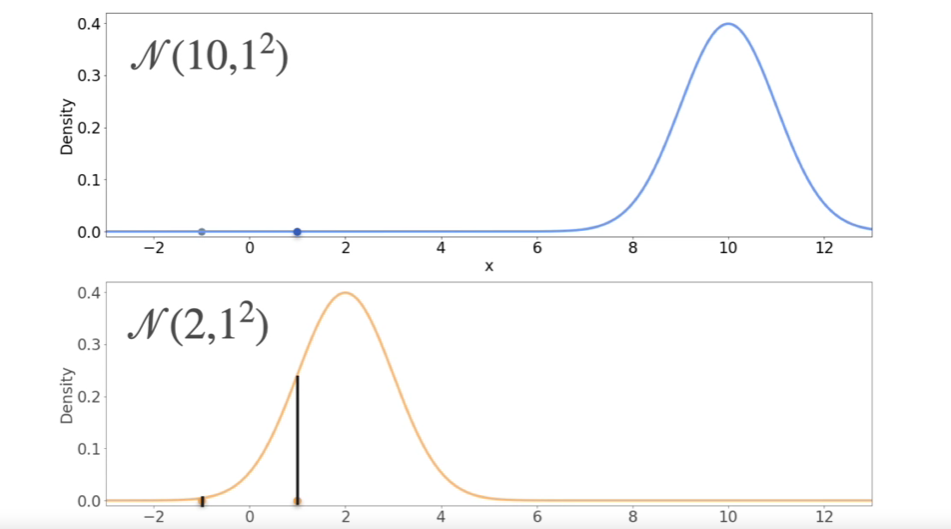
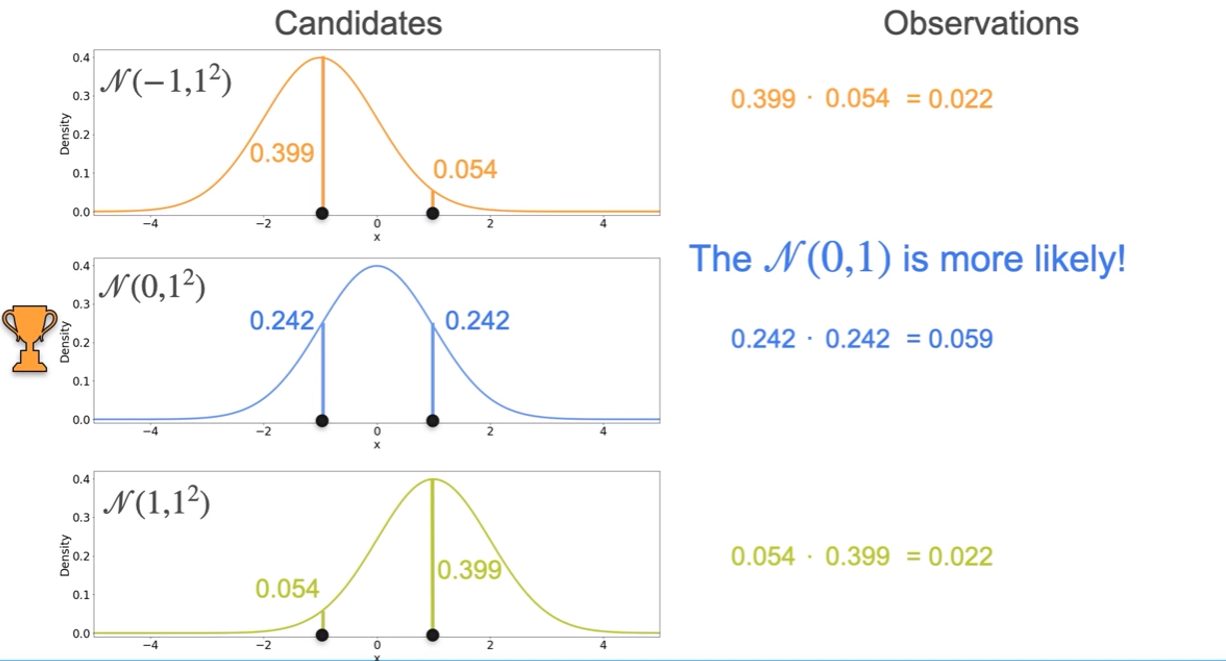
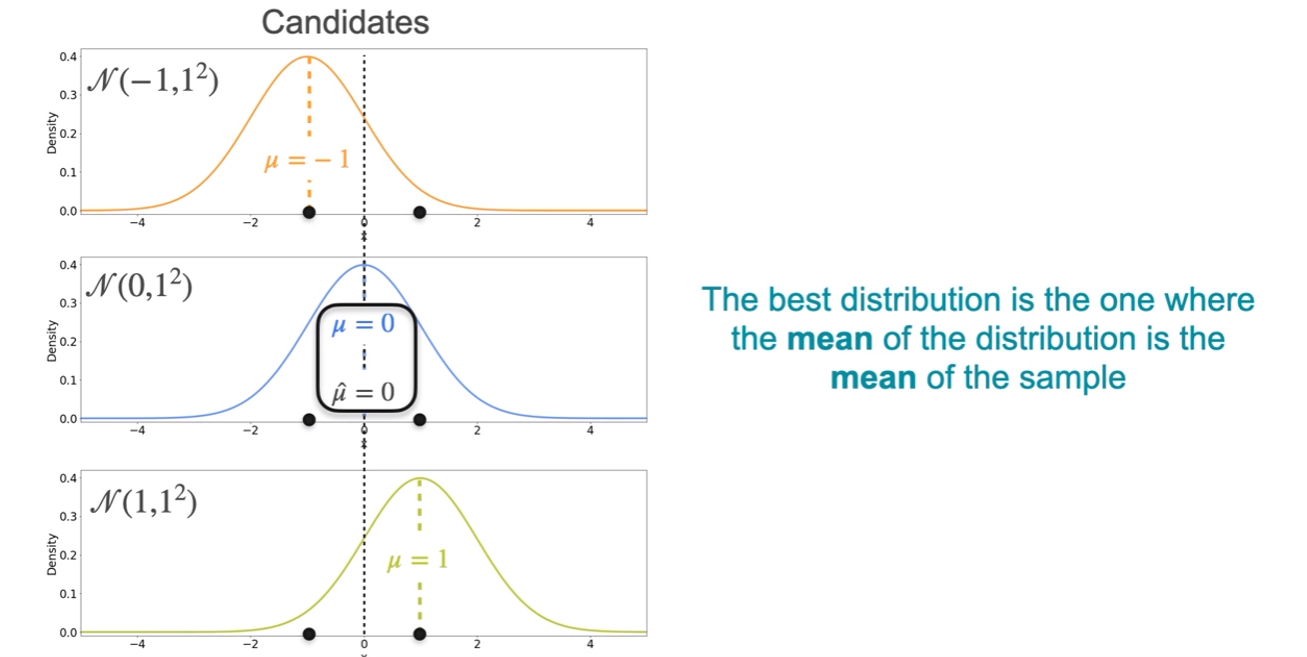
• given 1 and -1 second has more likelyhood.

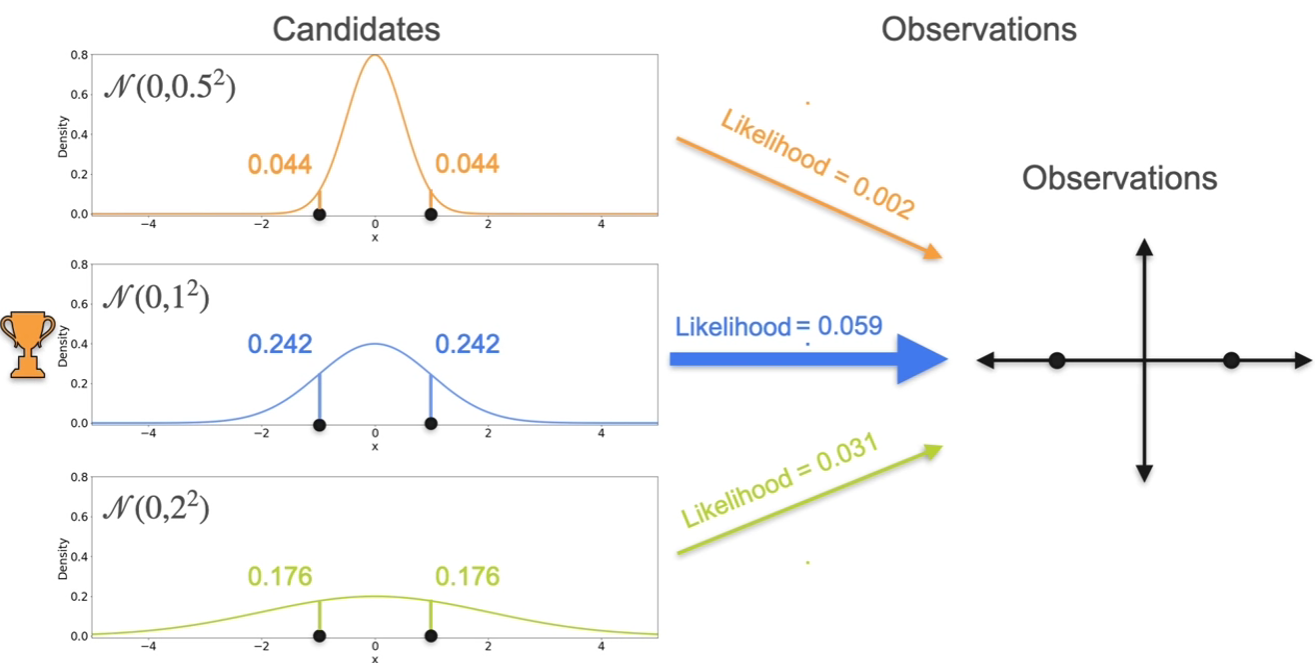
• what about 3 gaussians?

MLE: Linear Regression

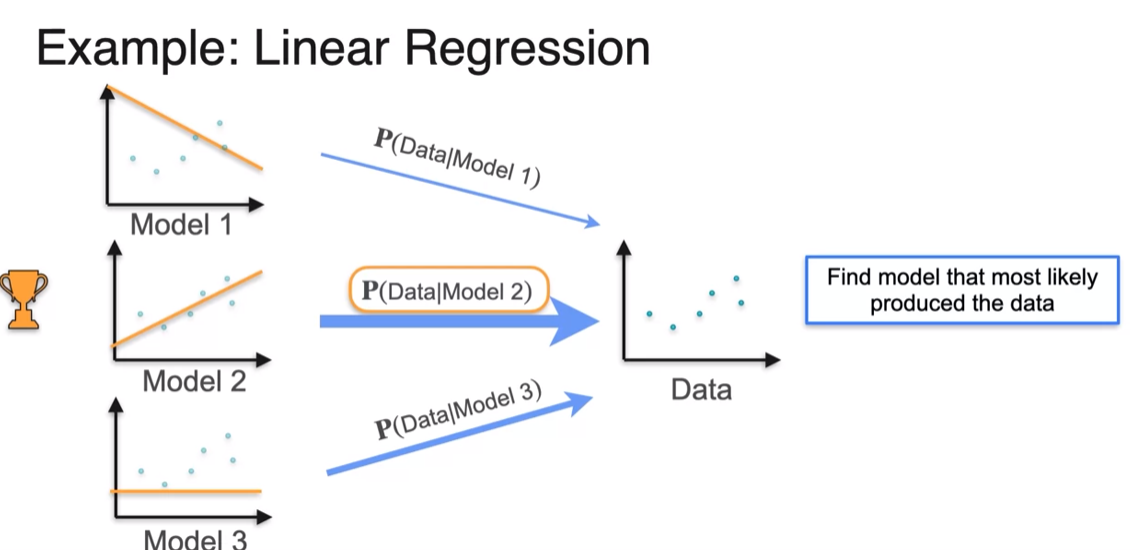
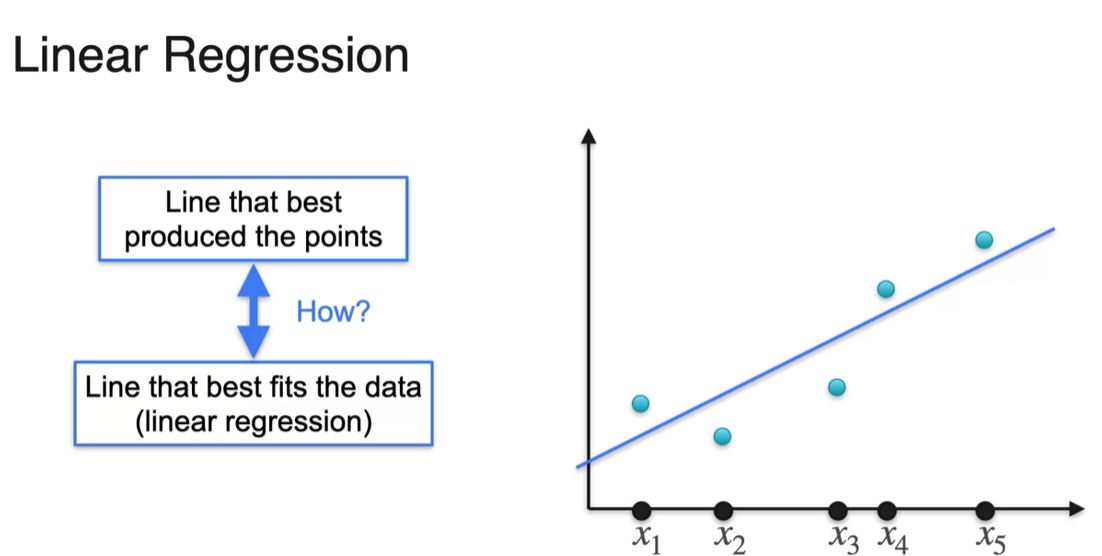
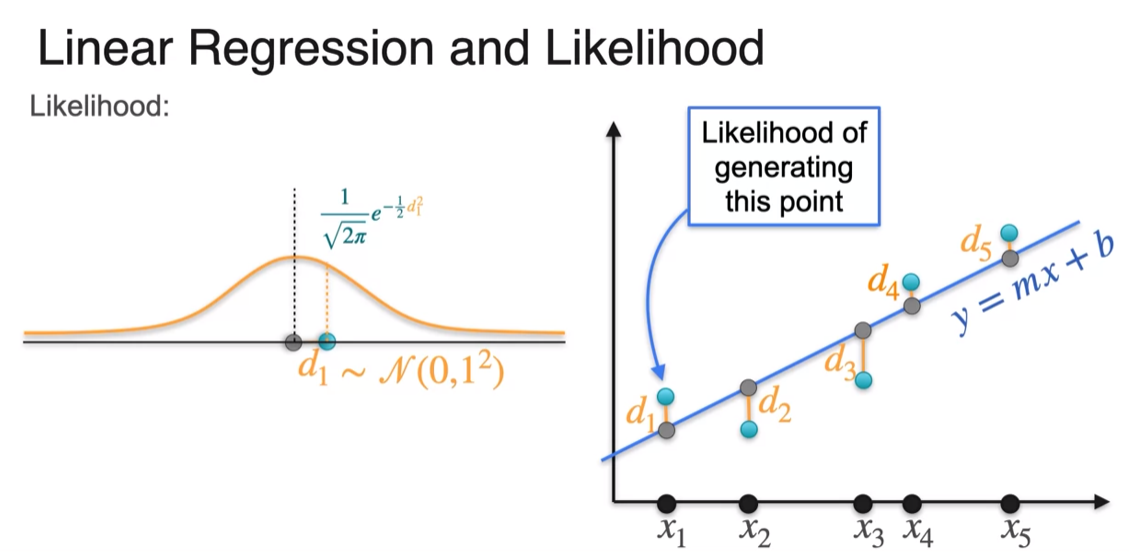
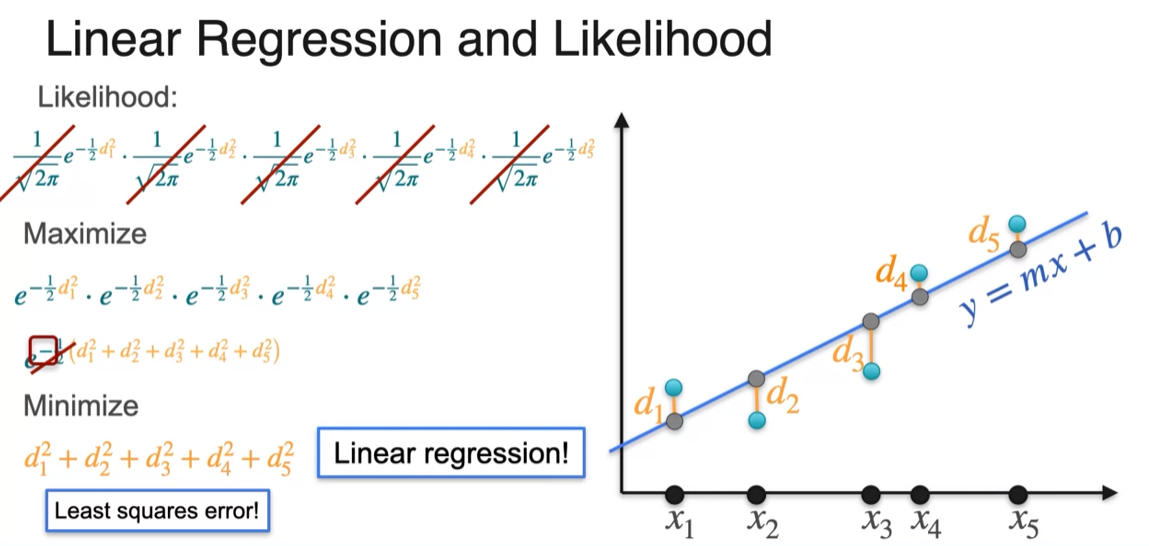
• finding the line most likely produce point using maximum likelihood is same as minimizing the leash square error using linear regression

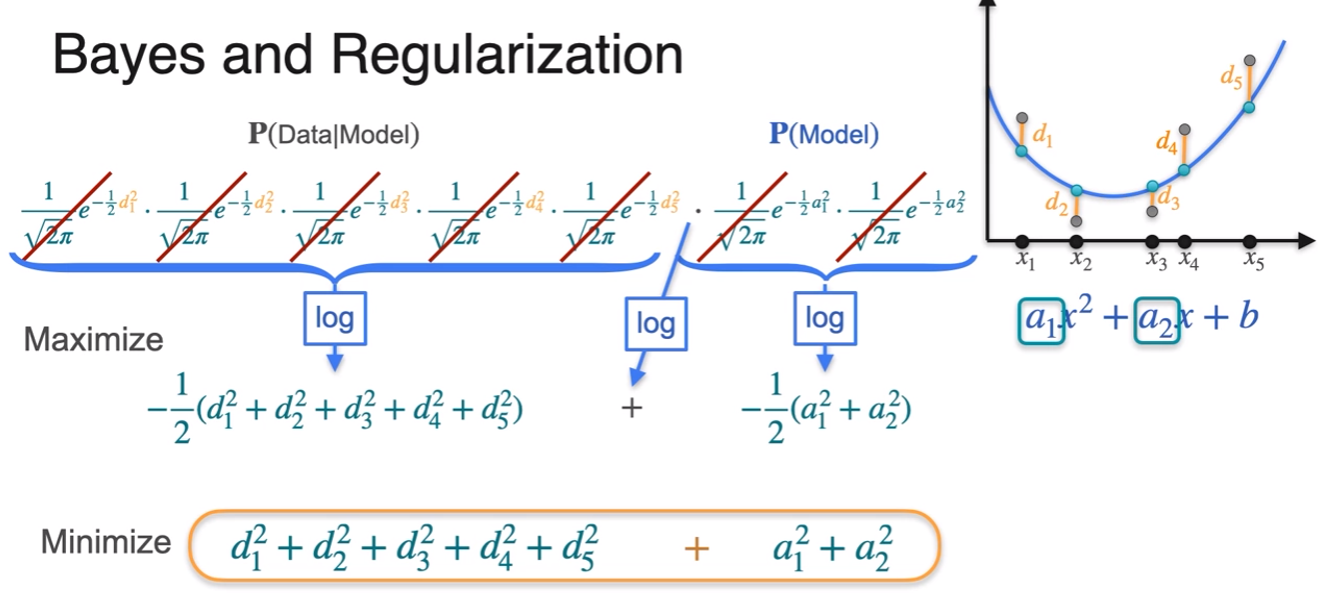
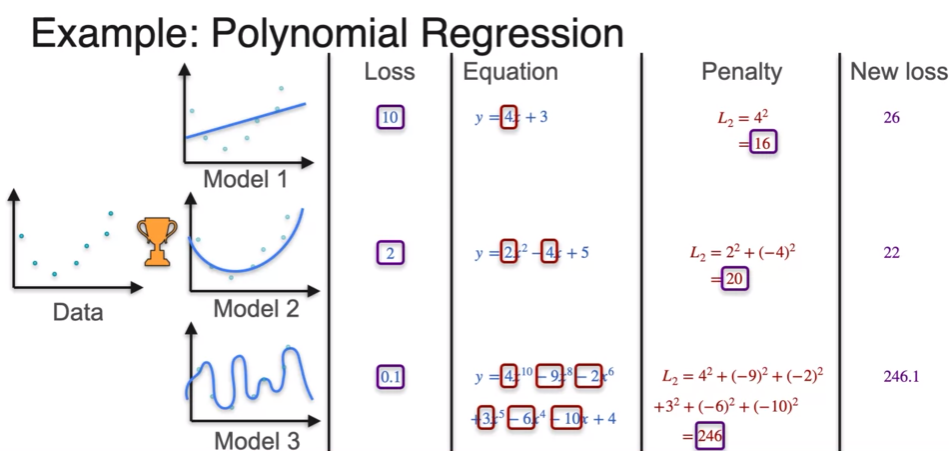
Regularization

Back to "Bayesics"

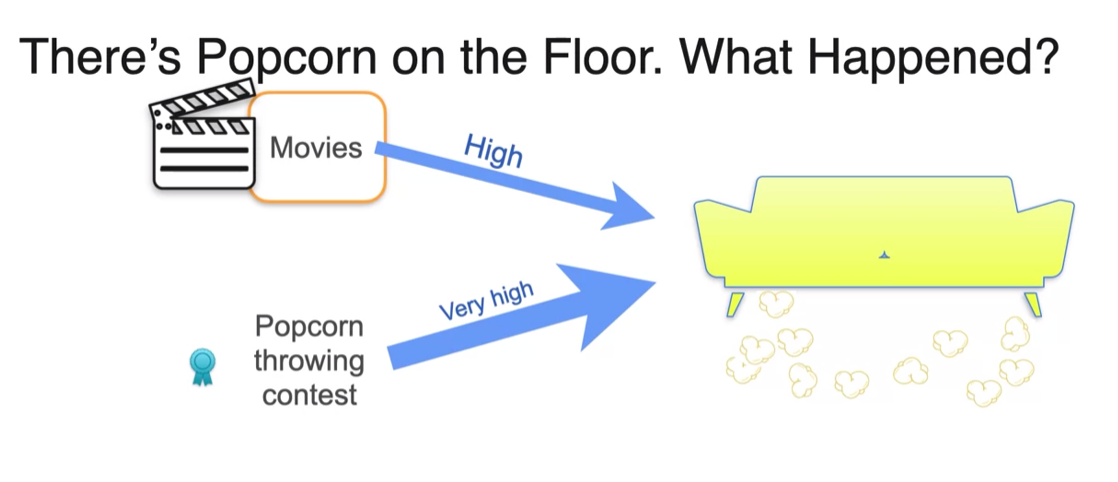
• Even though it's more likely generate the evidence, it's less likely to have happened on its own.

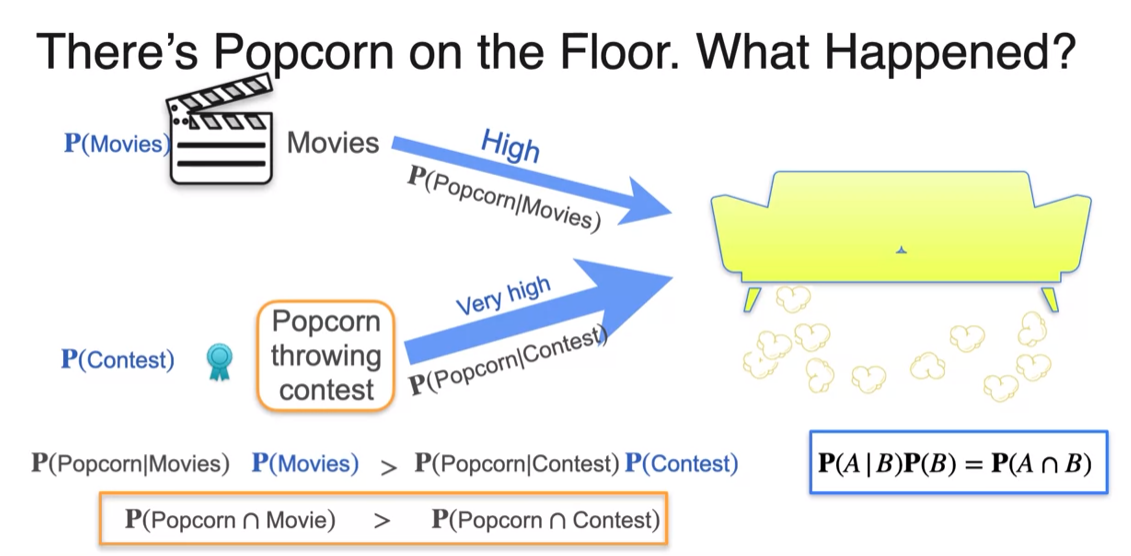
Bayesian Statistics - Frequentist vs. Bayesian

• Frequentist vs Bayesian
  빈도주의적 추론 vs 베이지안 추론

• all the point estimations follow a fequentist approach

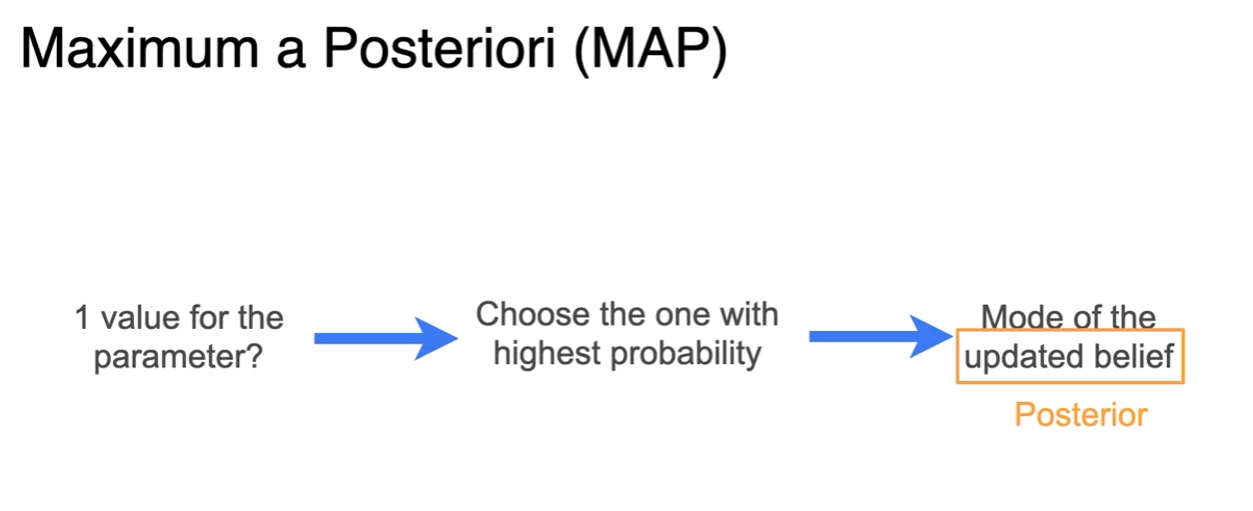
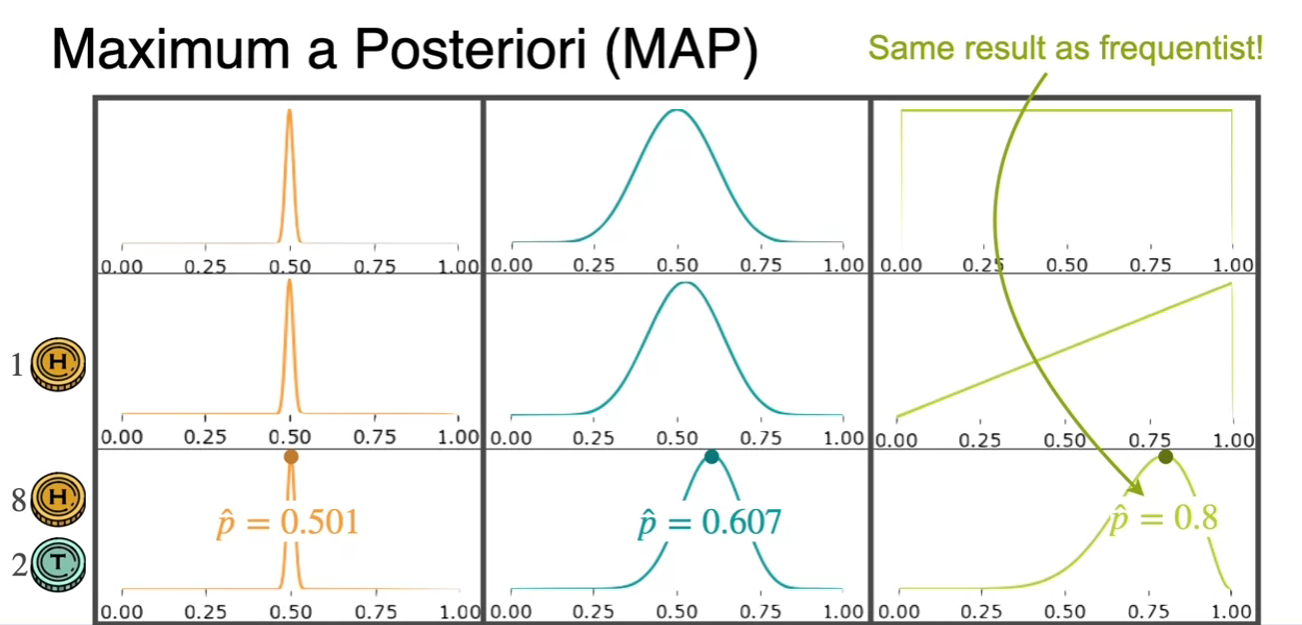
Bayesian Statistics - MAP

Bayesian Statistics - Updating Priors

• how to actually update belief

• all you're doing is taking your prior beliefs on the probability of an event and updating them to create new beliefs or posterior beliefs based on new evidence.

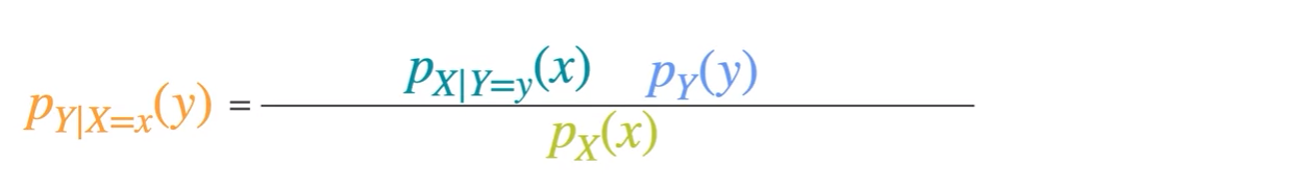
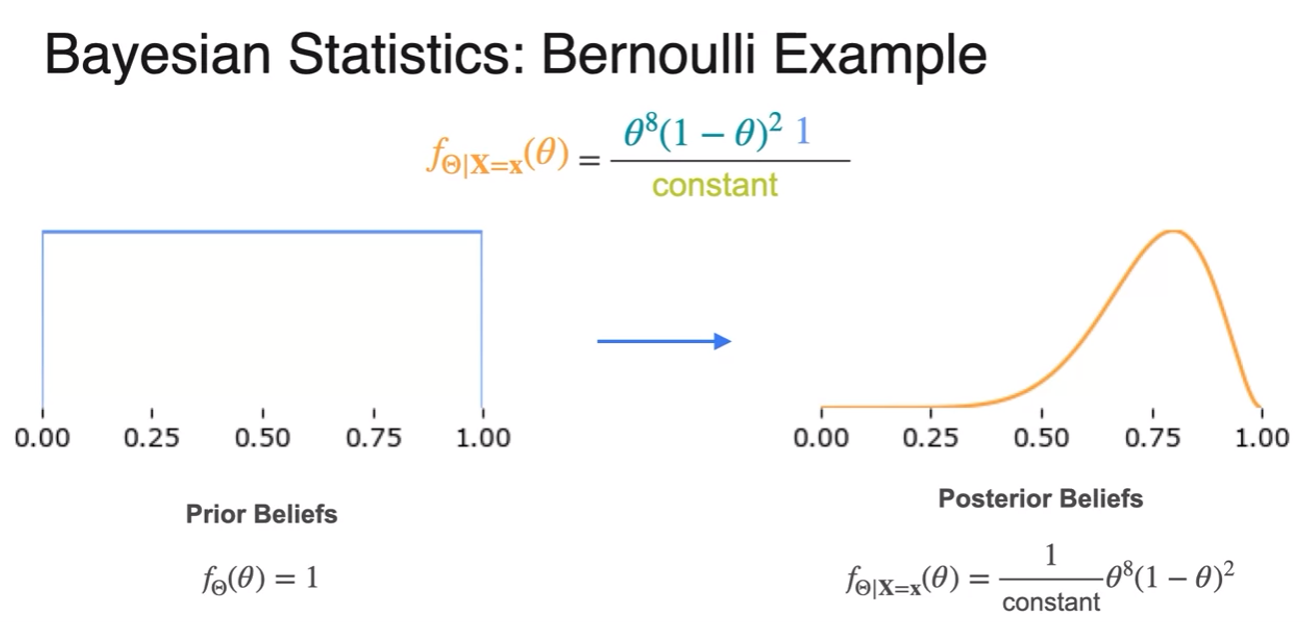
Bayesian Statistics - Full Worked Example

• cirano cheated the prior to make it easier
• this is Beta Distribution

• How your beliefs changed after considering the data.

• the value of theta that made the posterior maximum

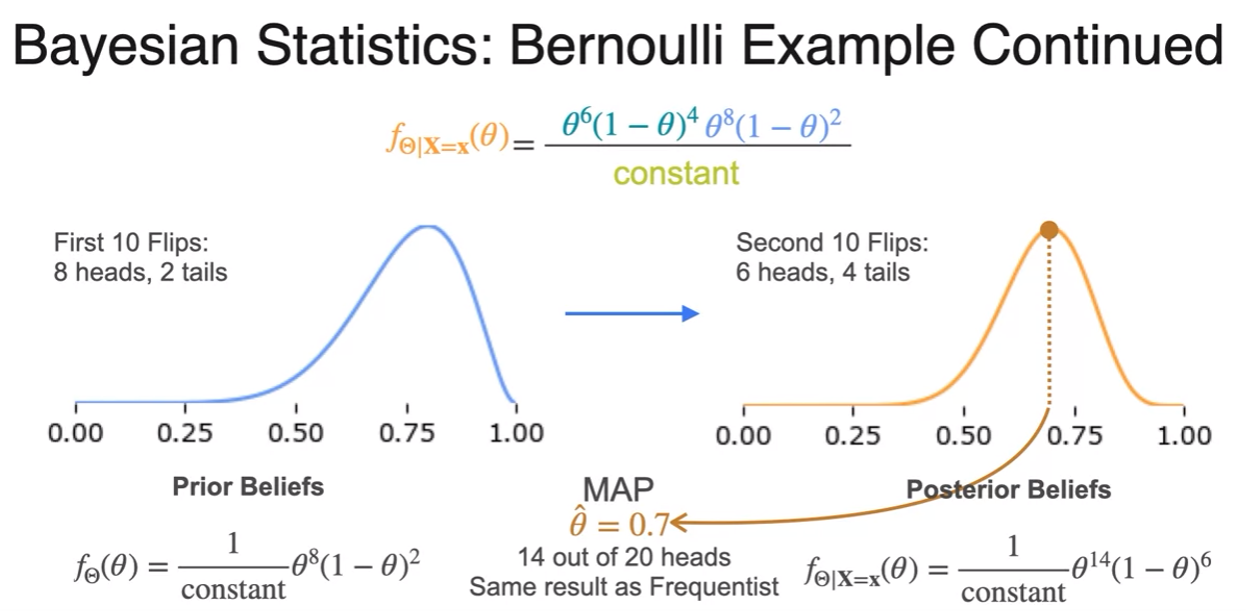
Relationship between MAP, MLE and Regularization

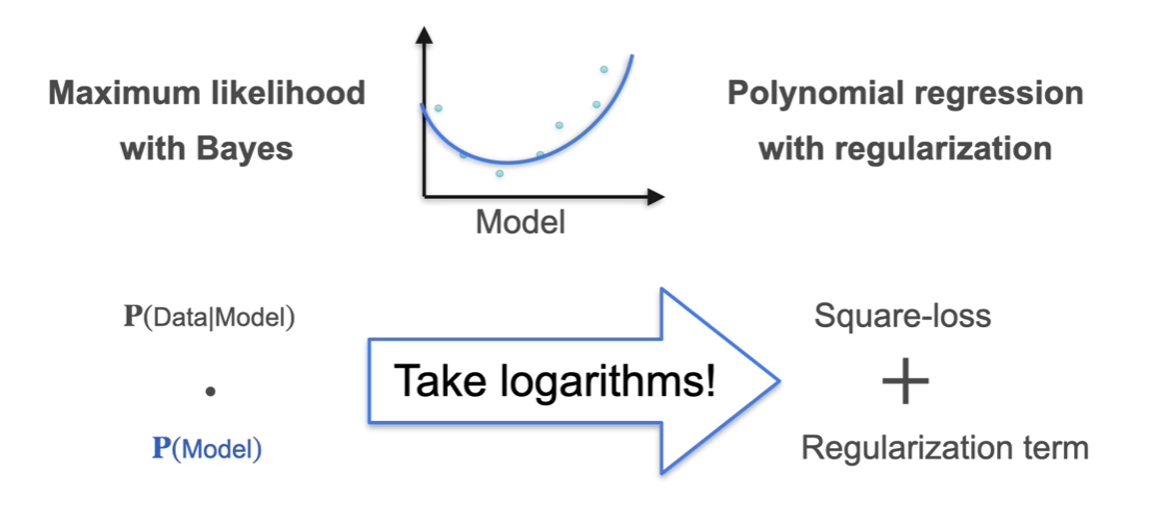
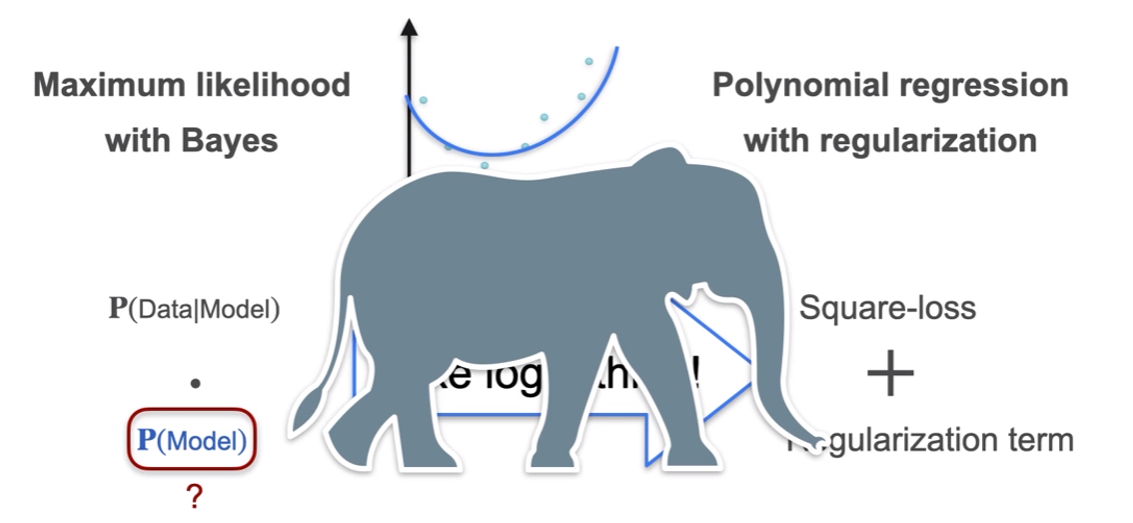
• Elephant in this room!

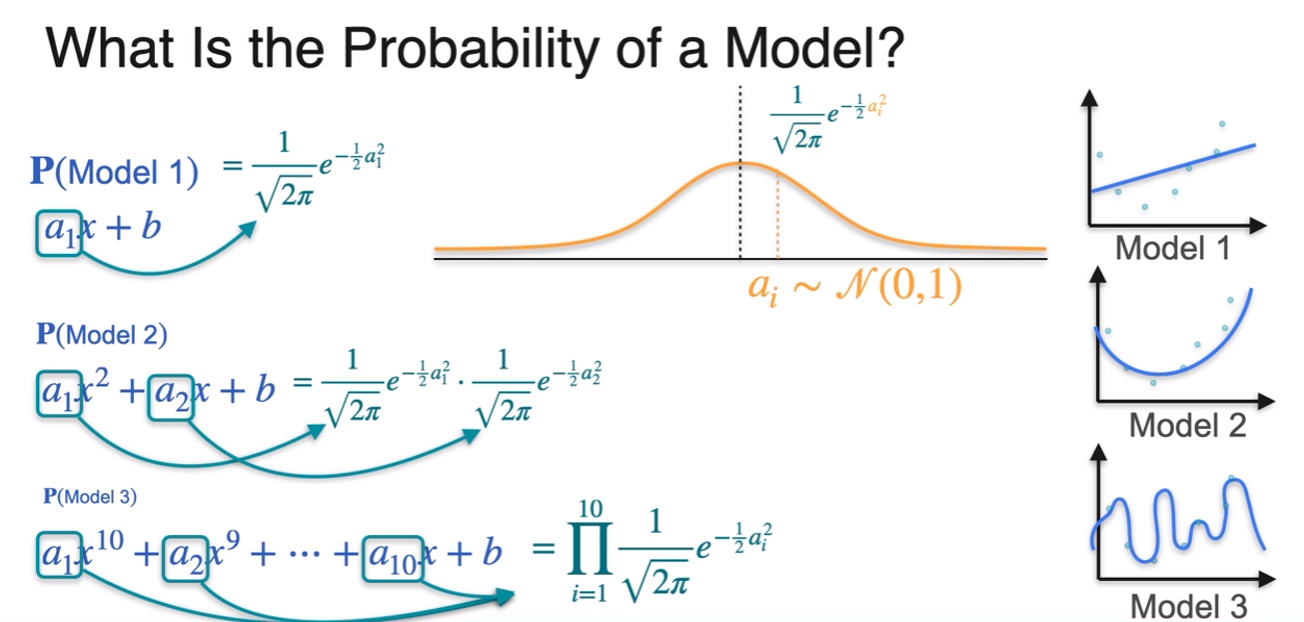
• a = likelyhood