오늘의 한 마디
드디어 최소 스패닝 트리를 배웠다.
- Baekjoon 문제 링크
- 현재 백준 문제집: 단기간 성장을 풀고 있습니다.
문제
그래프가 주어졌을 때, 그 그래프의 최소 스패닝 트리를 구하는 프로그램을 작성하시오.
최소 스패닝 트리는, 주어진 그래프의 모든 정점들을 연결하는 부분 그래프 중에서 그 가중치의 합이 최소인 트리를 말한다.
입력
첫째 줄에 정점의 개수 V(1 ≤ V ≤ 10,000)와 간선의 개수 E(1 ≤ E ≤ 100,000)가 주어진다. 다음 E개의 줄에는 각 간선에 대한 정보를 나타내는 세 정수 A, B, C가 주어진다. 이는 A번 정점과 B번 정점이 가중치 C인 간선으로 연결되어 있다는 의미이다. C는 음수일 수도 있으며, 절댓값이 1,000,000을 넘지 않는다.
그래프의 정점은 1번부터 V번까지 번호가 매겨져 있고, 임의의 두 정점 사이에 경로가 있다. 최소 스패닝 트리의 가중치가 -2,147,483,648보다 크거나 같고, 2,147,483,647보다 작거나 같은 데이터만 입력으로 주어진다.
출력
첫째 줄에 최소 스패닝 트리의 가중치를 출력한다.
예제 입력 1
3 3
1 2 1
2 3 2
1 3 3예제 출력 1
3발상
스패닝 트리 = 신장 트리
필자가 과거에 작성한 트리의 정의 내용에 따르면, 트리란 사이클이 없이 모든 정점이 연결되어있는 그래프다. 사이클이 없는 그래프이므로 정점의 개수가 V개이면 간선의 개수는 V-1개이다.
스패닝 트리는 트리의 정의와 크게 다를게 없다.
다만, 어떤 그래프의 부분 그래프를 지칭한다는 점에서 차이가 있다.
어떤 그래프(트리가 아니어도 됨)가 있고,
그 그래프의 모든 정점을 지나는 트리를 만들면, 그게 바로 스패닝 트리다.
Stack Overflow 글에 좋은 예시가 하나 있어서 가져와봤다.

위 사진에서 세번째에 나온 그래프는, 트리이긴 하지만 스패닝 트리는 아닌 예시다.
최소 스패닝 트리(Minimum Spanning Tree; MST)
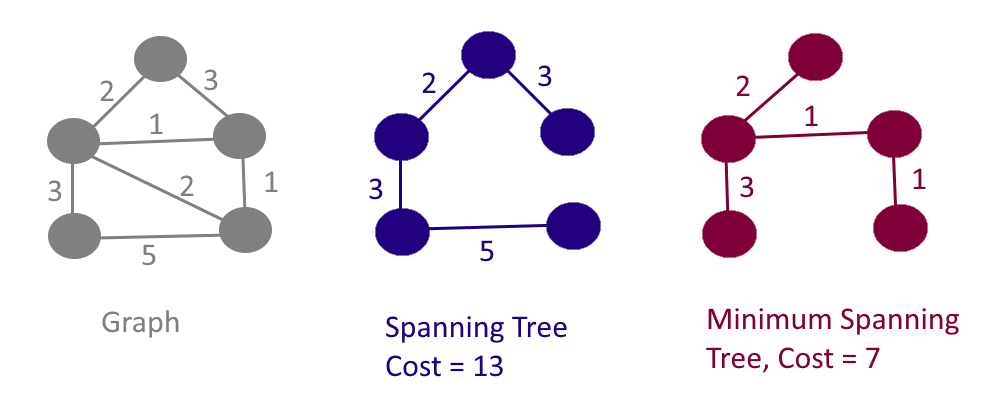
Graph에서 만들 수 있는 스패닝 트리의 예시가 두번째, 세번째에 나와 있다.
Graph에는 각 간선의 가중치가 주어져 있으며, 따라서 스패닝 트리 별로 가중치의 합 역시 얻을 수 있다.
최소 스패닝 트리는, 스패닝 트리의 가중치 합을 최소로 하는 스패닝 트리를 의미한다.
당연히 유일하다는 보장은 하지 못한다.
최소 스패닝 트리를 어디에다 쓰는지는...
백준 알고리즘 분류 - 최소 스패닝 트리 문제들을 참고하기 바란다.
크루스칼 알고리즘(Kruskal Algorithm)
최소 스패닝 트리를 구하는 방법은 다양하지만,
가장 대중적인 것이 바로 이번에 소개할 크루스칼 알고리즘이다.
이 링크에 시각화가 매우 잘 되어 있으니, 한번 보시길 추천한다.
알고리즘의 동작 과정을 설명하자면 다음과 같다.
- 모든 간선을 가중치 오름차순으로 정렬한다.
- 가중치가 가장 낮은 간선부터 순회하면서,
- 이 간선이 추가된다면 사이클을 발생시키는지 확인한다.
- 사이클을 발생시킨다면,
continue - 사이클을 발생시키지 않는다면 추가한다.
- 사이클을 발생시킨다면,
그렇게 모든 간선을 돌고 나면, 추가된 간선들이 바로 최소 신장 트리다.
사이클을 발생시키는지 확인하는 방법?
사이클이라고 하니까, 필자가 과거에 풀었던 문제 중에 백준 1956. 운동이라는 문제가 떠올랐다.
위 문제에서는 플로이드-워셜을 사용할 때 arr[i][i] 요소를 0이 아닌 INF로 초기화한 채 3중 for문을 돌리면 arr[i][i]에 (사이클이 발생할 경우) 사이클의 최소 가중치가 들어가 있는 방식으로 문제를 해결했다.
하지만 위 문제에서 정점은 400개 이하로 매우 적었고, 양수 가중치만 주어졌기 때문에 플로이드-워셜을 사용했던 것이다.
이번 최소 스패닝 트리 문제는 정점도 많고, 가중치가 음수가 될 수 있을 뿐 아니라, 근본적으로 스패닝 트리를 만드는 과정에서 간선이 바뀔 수 있기 때문에 플로이드-워셜로 푸는 것은 매우 부적절하다.
그 대신, 매우 직관적인 방법인 Union-Find를 활용한다.
n, m = map(int, sys.stdin.readline().rstrip().split())
parent = [i for i in range(n+1)]
def get_parent(x):
if parent[x] == x:
return x
parent[x] = get_parent(parent[x]) # get_parent 거슬러 올라가면서 parent[x] 값도 갱신
return parent[x]
def union_parent(a, b):
a = get_parent(a)
b = get_parent(b)
if a < b: # 작은 쪽이 부모가 된다. (한 집합 관계라서 부모가 따로 있는 건 아님)
parent[b] = a
else:
parent[a] = b
def same_parent(a, b):
return get_parent(a) == get_parent(b)이 알고리즘을 그대로 가져다 쓴다.
아래 풀이를 보면 매우 쉽게 이해할 수 있을 것이다.
풀이
import sys
input = lambda: sys.stdin.readline().rstrip()
V, E = map(int, input().split())
# Kruskal Algorithm
# https://techblog-history-younghunjo1.tistory.com/262
edges = []
for _ in range(E):
A, B, C = map(int, input().split())
edges.append((A, B, C))
edges.sort(key=lambda x: x[2]) # C(Cost)가 적은 것부터 정렬
# Union-Find
parent = [i for i in range(V+1)]
def get_parent(x):
if parent[x] == x:
return x
parent[x] = get_parent(parent[x]) # get_parent 거슬러 올라가면서 parent[x] 값도 갱신
return parent[x]
def union_parent(a, b):
a = get_parent(a)
b = get_parent(b)
if a < b: # 작은 쪽이 부모가 된다. (한 집합 관계라서 부모가 따로 있는 건 아님)
parent[b] = a
else:
parent[a] = b
def same_parent(a, b):
return get_parent(a) == get_parent(b)
answer = 0
for a, b, cost in edges:
# cost가 작은 edge부터 하나씩 추가해가면서 같은 부모를 공유하지 않을 때(사이클 없을 때)만 확정
if not same_parent(a, b):
union_parent(a, b)
answer += cost
print(answer)