[CS:APP] Horner의 방법이 더 느리다?

발상 출처 : 컴퓨터 시스템 제3판(김형신 역), pp.508-509

CS:APP는 원저 제목인 Computer Systems : A Programmer's Perspective의 줄임말입니다.

Horner의 방법(호너의 방법; Horner's Method)

Horner의 방법은 다항식(polynomial)의 결과를 더 적은 연산 수로 도출해내려 할 때 쓰인다.

연산 수가 적으면 연산 시간도 단축되는 것이 일반적이기 때문에, 이런 최적화 기법들은 컴퓨터공학에서 다루어지는 주제 중 하나이다.

컴퓨터공학에서는 계수를 a, b, c가 아니라 별도의 배열에 차수에 대응하여 a[0], a[1], a[2]와 같이 저장하는 것이 일반적이므로, 다항식을 다음과 같이 표현할 수도 있다.

함께 P(x)를 계산하는 알고리즘을 짜보자.

1. 기본 방법

double calculatePolynomial(double a[], double x, long degree)
{
    double result;
    double x_power;
    
    result = 0;
    for (long i = 0; i <= degree; i++) {

        x_power = 1;
        for (long j = 1; j <= i; j++)
            x_power *= x;
        
        result += a[i] * x_power;        
    }
    return result;
}

편의상 degree를 n으로 표현한다.

• 덧셈은 result +=에서만 사용되기 때문에, n+1회 사용된다.
• 곱셈은 result +=에서도 사용되기 때문에, 일단 n+1회 사용된다.
  • 더하여 x_power를 계산하는 데에도 사용되기 때문에, 0 + 1 + 2 + ... + n회 사용되며,

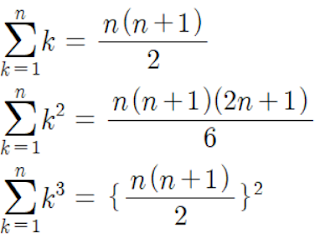
에 따라 n(n+1) / 2회로 바꾸어 쓸 수 있다.

• 정리하면, 덧셈은 n+1회, 곱셈은 (n(n+1) / 2) + n+1회 사용된다.

2. x_power 캐싱

이미 깨달았겠지만, 매번 x_power를 계산할 필요가 전혀 없다.

double calculatePolynomial(double a[], double x, long degree)
{
    double result;
    double x_power;
    
    result = 0;
    x_power = 1;
    for (long i = 0; i <= degree; i++) {
        result += a[i] * x_power;
        x_power *= x;
    }
    return result;
}

저번까지 계산했던 x_power에 x만 한 번 곱해주면, 다음번 루프에서 사용할 x_power가 되기 때문이다.

• 덧셈은 위와 같이 n+1회 사용된다.
• 곱셈은 n+1회가 두번 사용될 뿐이다. 즉, 2n+2회 사용된다.

곱셈 횟수를 O(n^2)에서 O(n)으로 줄였다! 아주 획기적인 발전이다

2.5. a[0]만 루프에서 빼기

double calculatePolynomial(double a[], double x, long degree)
{
    double result;
    double x_power;
    
    result = a[0];
    x_power = x;
    for (long i = 1; i <= degree; i++) {
        result += a[i] * x_power;
        x_power *= x;
    }
    return result;
}

뭐... 최적화라고 하기도 부끄럽다.
result에 0 대신 a[0]으로 시작해버리면서 루프를 그저 1회 줄였다.

• 덧셈은 n회 사용된다.
• 곱셈은 2n회 사용된다.

3. Horner의 방법

여기서 곱셈 횟수를 더 줄이는 방법이 바로 Horner의 방법이다.

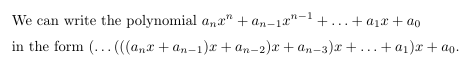
같은 다항식을 위의 방법으로 바꾸어 쓸 수 있다!

처음에는 굉장히 비직관적으로 보이겠지만, 풀어서 계산해보면 똑같은 식이 된다는 것을 알 수 있다.

이렇게 굳이 바꾸어 표현하는 이유가 있냐고 물어본다면, 알고리즘으로 짜보면 그 이유를 알 수 있다.

double calculatePolynomial(double a[], double x, long degree)
{
    double result;
    
    result = a[degree];
    for (long i = degree-1; i >= 0; i--)
        result = a[i] + x*result;
    return result;
}

천천히 살펴보면 다음과 같은 과정을 반복한다.

1. a_(n-1) + x*a_n을 계산한다.
2. 그 값에 x를 곱한 뒤 a_n-2를 더한다.
   (후략)

• 덧셈은 n회 사용된다.
• 여기서 핵심은 곱셈도 n회 사용된다는 점이다!

무려 곱셈을 n번이나 줄였다!!

---

Ver 2.5와 Horner의 방법 소요시간 비교

코드

#include <time.h>
#include <stdio.h>
#include <stdlib.h>

#define DEGREE 424242
#define ATTEMPT 4242

double generate_random_real_number(void); // 0.0 ~ 100.0

double poly(double a[], double x, long degree);
float calculate_poly_elapsed_time(double a[], double x, long degree);

double poly_horner(double a[], double x, long degree);
float calculate_poly_horner_elapsed_time(double a[], double x, long degree);

int main(void)
{
	double a[DEGREE];
	for (int i = 0; i < DEGREE; i++)
		a[i] = generate_random_real_number();

	float diff1, diff2;
    float sum1 = 0, sum2 = 0;

	for (int i = 1; i <= ATTEMPT; i++) {
		diff1 = calculate_poly_elapsed_time(a, 42, DEGREE);
		diff2 = calculate_poly_horner_elapsed_time(a, 42, DEGREE);

        printf("[Attempt %4d] Ver2.5 -> %.3fms  |  Horner -> %.3fms\n", i, diff1, diff2);

		sum1 += diff1;
		sum2 += diff2;
	}
    float avg1 = sum1 / ATTEMPT;
    float avg2 = sum2 / ATTEMPT;

    printf("\n");
    printf("============== RESULT ===============\n");
	printf("Version 2.5 Elapsed Time Average : %.3fms\n", avg1);
	printf("Horner's Method Elapsed Time Average : %.3fms \n", avg2);
    printf("\n");
    printf("%.3f / %.3f = %.3fx\n", avg2, avg1, avg2 / avg1);
}

double poly(double a[], double x, long degree)
{
    double result;
    double x_power;
    
    result = a[0];
    x_power = x;
    for (long i = 1; i <= degree; i++) {
        result += a[i] * x_power;
        x_power *= x;
    }
    return result;
}

double poly_horner(double a[], double x, long degree)
{
    double result;
    
    result = a[degree];
    for (long i = degree-1; i >= 0; i--)
        result = a[i] + x*result;
    return result;
}

float calculate_poly_elapsed_time(double a[], double x, long degree)
{
	clock_t start, end;

	start = clock();
	poly(a, x, degree);
	end = clock();
    return (end - start) / 1000.0;
}

float calculate_poly_horner_elapsed_time(double a[], double x, long degree)
{
	clock_t start, end;

	start = clock();
	poly_horner(a, x, degree);
	end = clock();
    return (end - start) / 1000.0;
}

double generate_random_real_number(void) // 0.0 ~ 100.0
{
	srand(time(NULL));
	return (rand() / (double)RAND_MAX) * 100.0;
}

결과

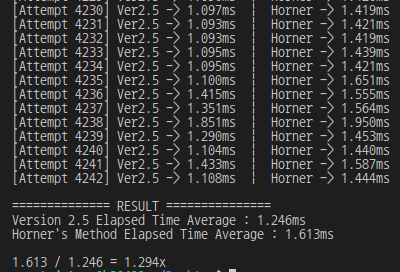
degree가 충분히 큰 상태(위의 코드에서는 degree = 424242)라면, 연산 횟수에 차이가 크게 발생하므로 연산 시간도 줄어들 것이라고 생각했지만 결과는 정반대였다.

double poly(double a[], double x, long degree)
{
    double result;
    double x_power;
    
    result = a[0];
    x_power = x;
    for (long i = 1; i <= degree; i++) {
        result += a[i] * x_power;
        x_power *= x;
    }
    return result;
}

덧셈을 n번 하고, 곱셈을 2n번 했던 Version 2.5의 평균 소요시간은 1.246ms,

double poly_horner(double a[], double x, long degree)
{
    double result;
    
    result = a[degree];
    for (long i = degree-1; i >= 0; i--)
        result = a[i] + x*result;
    return result;
}

덧셈을 n번 하고, 곱셈도 n번 했던 Horner의 방법 알고리즘의 평균 소요시간은 1.613ms로 나타났다. 즉, Horner의 방법이 1.294배 더 느린 것이다.

과연 이유가 무엇일까?

---

처리량 경계값

CS:APP
- Chapter 5 프로그램 성능 최적화하기
  - 5.7 최신 프로세서 이해하기
  	- 5.7.2 기능 유닛의 성능(pp.501-503)

그 이유를 쉽게 표현하자면, 꼭 이전 연산이 끝나야만 다음 연산을 시작할 수 있는 건 아니다라는 점인데...

이에 대해 더 자세히 알아보기에 앞서, 먼저 알아두어야 할 지식에 대해 짚고 넘어가자.

지연시간 경계값, 처리량 경계값

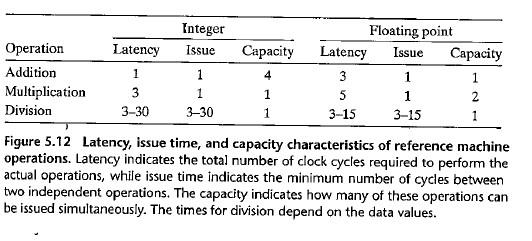
최신 프로세서에는 지연시간 경계값(latency bound)과 처리량 경계값(throughput bound)라는 두 가지 값을 갖는다.

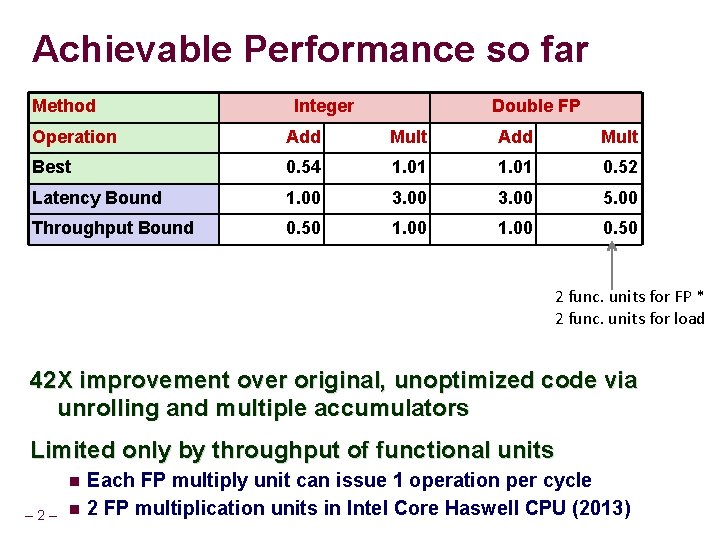
여기서의 지연시간이란, 해당 연산을 수행하는데 소요되는 전체시간을 의미한다.

위의 표에 따르면,

• 정수 덧셈의 경우 지연시간 경계값은 1.0, 처리량 경계값은 0.5,
• 정수 곱셈의 경우 지연시간 경계값은 3.0, 처리량 경계값은 1.0이다.
  (여기서 3.0이란 클럭이 3번 돌아야 연산이 완료된다는 뜻이다.)

어떻게 정수 덧셈 하나를 수행하는데 1.0이 걸리는데, 0.5 의 처리 속도를 만들 수 있단 말인가?
그리고 정수 곱셈 하나를 수행하는데 3.0이 걸리는데, 1.0의 처리 속도를 만들 수 있단 말인가?

그 이유는 위에서 말한 것처럼 꼭 이전 연산이 끝나야만 다음 연산을 시작할 수 있는 건 아니기 때문이다.

위 두 사진의 차이를 보고 감이 왔길 바란다.
이러한 방식을 두고 파이프라인이라고 한다.

발급 시간, 용량

여기서 우리는 또 다른 개념인 발급 시간(issue time)과 용량(capacity)에 대해 잠깐 짚고 넘어갈 필요가 있다.

정수 연산의 경우 지연시간은 위에서 살펴봤던 것처럼 덧셈은 1.0, 곱셈은 3.0이다.

하지만 위의 Instruction Pipeline 사진처럼 연산 여러개를 병렬적으로 수행하는 것이 가능하며, 정수 덧셈을 여러번 수행한다고 했을 때 첫번째 인스트럭션을 넣고 발급 시간만 지나면 첫번째 덧셈이 끝나지 않았다 하더라도 두번째 덧셈을 수행시킬 수 있다!

정수 덧셈은 어차피 지연시간이 1.0이라서 발급시간 득을 크게 못 보겠지만,
정수 곱셈의 경우 3.0을 다 기다릴 필요 없이 1.0만 지나면 두번째 곱셈을 시작시킬 수 있다는 점에서 매우 유리하다고 할 수 있다.

충분히 큰 횟수로 반복 실행되는 경우에 연산 당 평균 수행시간은, 지연시간은 거의 무시되고 발급시간에 수렴할 것이다.

두번째로 살펴볼 개념은 용량이다.

용량(capacity)이란 해당 연산을 수행할 수 있는 함수 유닛의 수를 나타낸다.
즉, 정수 덧셈의 경우 4개의 함수 유닛을 동시에 수행하는 것이 가능하며, 따라서 한 클럭 사이클 당 4개의 정수 덧셈을 수행할 수 있다. (하지만 실제로는 프로세서 제한으로 2개까지만 가능하다.)

처리량 경계값 구해보기

따라서 처리량 경계값은, 지연시간이 아니라 발급시간을 기준으로 하며, 용량이 1보다 크면 그 용량으로 나누어 계산할 수 있다.

• 정수 덧셈의 발급시간은 1.0, 용량은 4이지만 2로 제한되므로, 처리량 경계값은 1.0 / 2 = 0.5이다.
• 정수 곱셈의 발급시간은 1.0, 용량은 1이므로, 처리량 경계값은 1.0이다.

---

코드를 데이터흐름 그래프로 바꾸기

CS:APP
- Chapter 5 프로그램 성능 최적화하기
  - 5.7 최신 프로세서 이해하기
  	- 5.7.3 프로세서 동작의 추상화 모델(pp.503-508)

이제 우리는 인스트럭션 파이프라인이라는 발상에 대하여 이해했다.

그렇다면 아래 두 함수를 최대한 병렬적으로 실행해보자.

double poly(double a[], double x, long degree)
{
    double result;
    double x_power;
    
    result = a[0];
    x_power = x;
    for (long i = 1; i <= degree; i++) {
        result += a[i] * x_power;
        x_power *= x;
    }
    return result;
}

double poly_horner(double a[], double x, long degree)
{
    double result;
    
    result = a[degree];
    for (long i = degree-1; i >= 0; i--)
        result = a[i] + x*result;
    return result;
}

p.551 해설
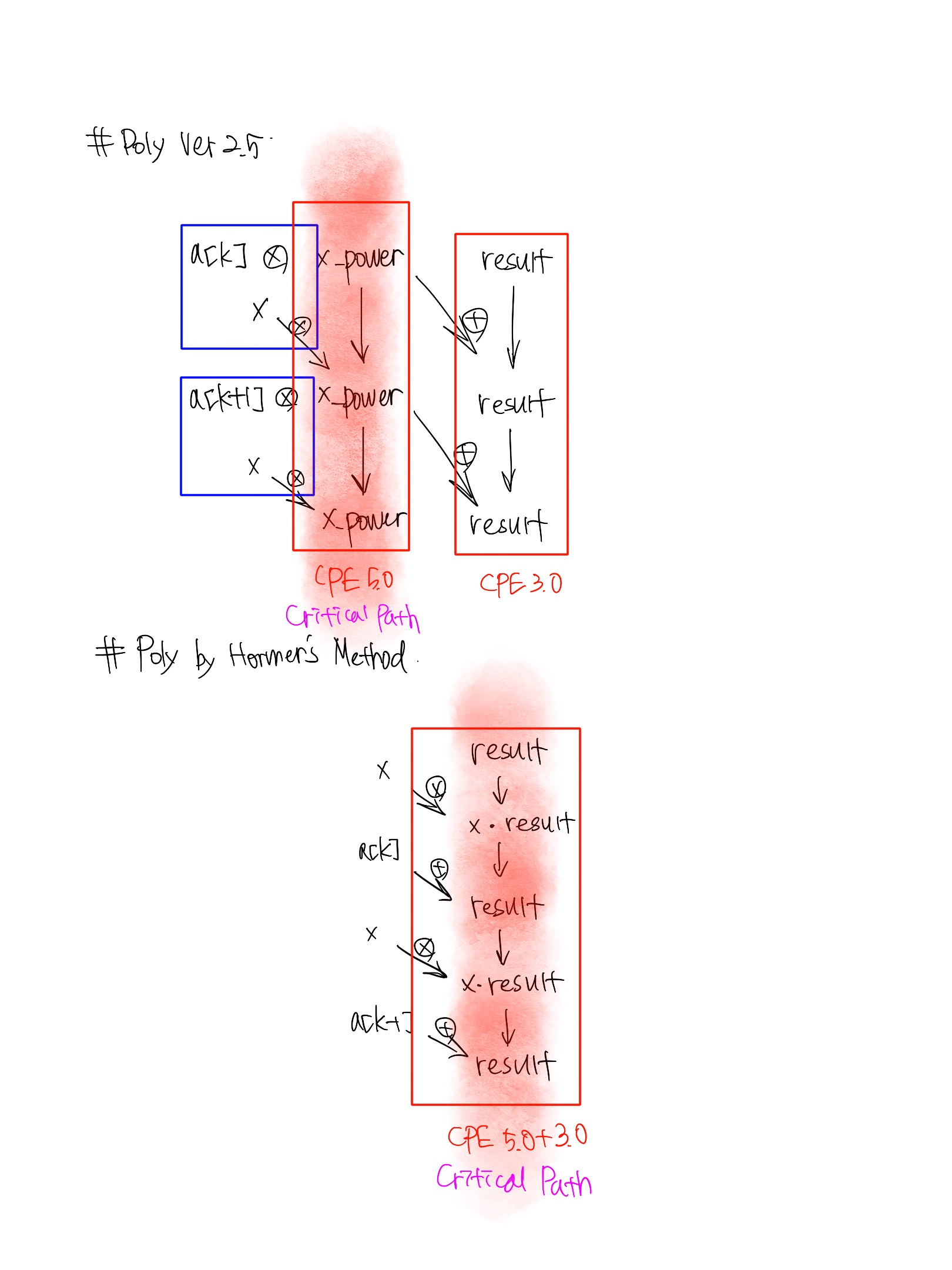
Poly Ver 2.5의 경우, 성능제한 계산은 반복되는 수식 x_power = x*x_power이라는 것을 알 수 있다. 이 수식으로 인해 부동소수점 곱셈(5클럭 사이클)은 이전 반복실행에 대한 계산이 완료될 때까지 시작할 수 없게 된다. result의 갱신을 위해서 부동소수점 덧셈(3클럭 사이클)이 연속되는 반복실행들 사이에 이루어져야 한다.

p.552 해설
Poly Horner에서 성능을 제한하는 계산은 수식 result = a[i] + x*result의 반복적인 계산부분이라는 것을 알 수 있다. 이전 반복실행의 결과인 result 값으로 시작해서 먼저 이 값에 x를 곱하고(5클럭 사이클), 그러고 나서 이번 반복실행에 대한 값을 갖기 전에 a[i]에 그 결과를 더한다(3클럭 사이클). 그래서 매 반복실행은 최소 지연시간 8사이클이 소요된다.

즉, Poly Ver 2.5는 매 반복실행마다 한 번이 아니라 두 번의 곱셈이 필요하지만, 반복실행마다 핵심 경로를 따라서 단 한 번의 곱셈만이 일어난다.

따라서 Horner의 방법이 오히려 느리다!

내가 공부하면서 애매한 점 : result = a[i]*x_power + result랑 result = a[i] + x*result 둘 다 CPE 8.0으로 보이는데, 앞의 식에서의 a[i]*x_power는 CPE 산정에 안 들어 가서 CPE 3.0으로 계산되는 이유가 무엇일까?