[컴퓨터 비전] ✨Optical Flow Lukas Kanade Method 중심의 개념 & OpenCV 구현 ✨

목차

• Optical Flow란?
• Lucas-Kanade(LK) method
  • Lucas-Kanade Improved: Iterative Lucas-Kanade
  • Lucas-Kanade Improved: Pyramidal Lucas-Kanade Method
• Dense Optical Flow (Farnebäck Optical Flow)
• 관련 논문 모음
• OpenCV 구현 (end-to-end, SOTA 위주)
• 참고 자료

Optical Flow란?

Optical Flow는 이미지의 빛의 패턴의 가시적인 움직임을 말한다. 카메라와 움직임과 물체의 움직임이 영향을 줄 수 있다. Optical flow를 계산하기 위해서는 이미지들 사이에 시간적 연속성과 이미지 내의 점들과 그 이웃하는 점들 사이의 공간적인 연속성이 있다는 가정이 필요하다. Optical flow는 이차원 Vector field의 모습으로 표현된다 (3D로 표현하는 접근도 있다. 아래 논문 소개에서 간단히 다룬다). 말은 어렵지만, 아래 optical flow가 탐지된 그림을 보면 이해가 쉽다. 아래 그림은 OpenCV 라이브러리를 활용해 영상에서 몇몇 포인트들의 Optical flow 즉, 움직임을 그린 것이다.

Optical Flow는 움직임을 탐지하는 것과 관련된 motion segmentation을 비롯해 비디오 인코딩과 같은 많은 분야 까지 폭넓게 적용될 수 있다.

Lucas-Kanade(LK) Method

Lucas-Kanade 방식은 영상 내 이미지 사이의 시간적, 공간적 연속성과 이웃한 픽셀들의 움직임은 함께 간다는 것을 가정하고 만들어졌다.
우리는 연속된 이미지에서 우리가 관측하고 있는 포인트 p의 변위를 알고 싶다. 이 때, 연속성을 이용하여 delta t만큼의 시간이 지날 동안 $\vartriangle$p 만큼의 변위가 있었다고 가정할 수 있고, 이미지의 함수 f를 풀어 변위를 구할 수 있다.

$f(p - \vartriangle p, t) = f(p, t + \vartriangle t)$
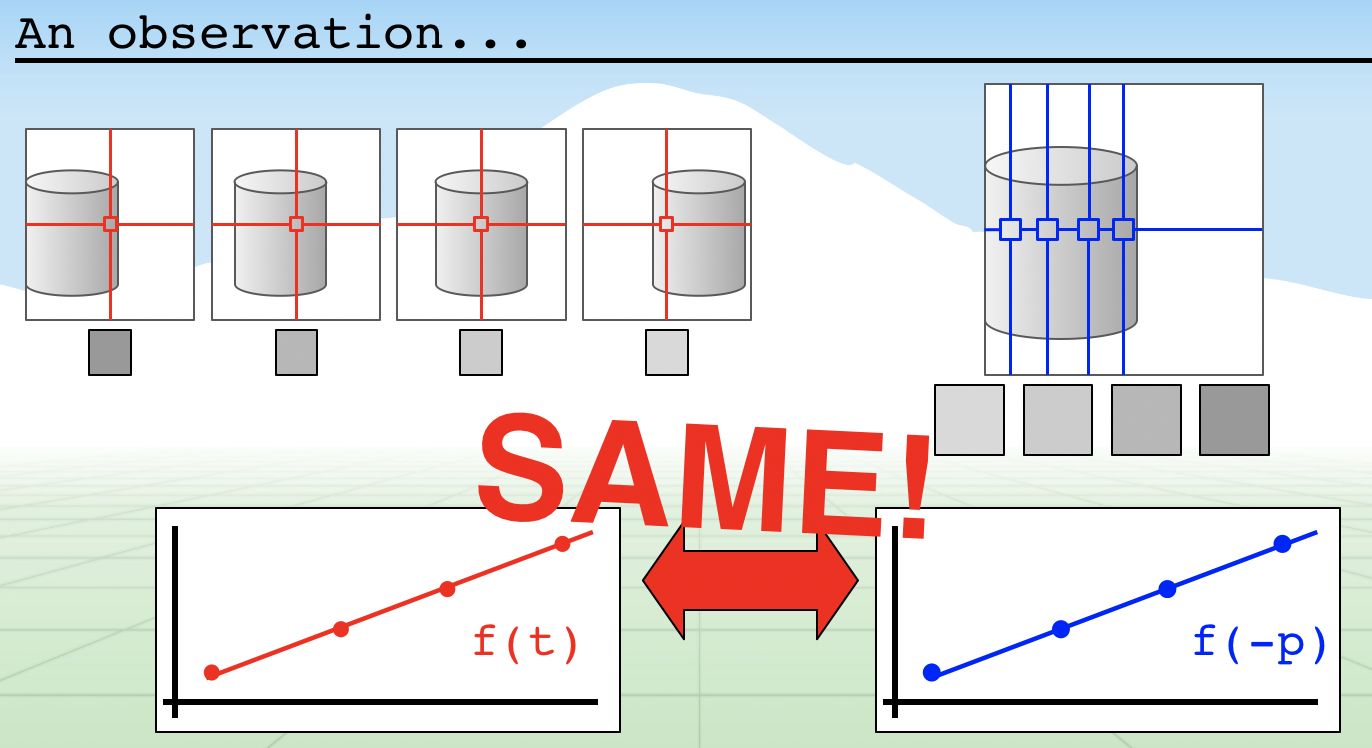이미지 출처: The Ancient Secrets of Computer Vision 8강

하지만, 이 경우 계산이 복잡해진다는 문제가 있다. Lucas-Kanade Method에서는 Taylor Expansion을 이용해 이 함수를 n차수의 다항수로 근사하는 방식을 말한다. Taylor expansion은 아래 식으로 나타낼 수 있다.
f(x) ~ $\sum_{i}a_ix^i$ Equal at x

Lucas-Kanade에서는 1차 다항식으로 함수를 근사한다. t 시점에서 변위 x에 따른 함수 f(x,t) ≈ mx + b 라고 근사한 것이다. m은 해당 포인트에서의 derivative = gradient이다!

mp - m𝚫p + b - f(p, t) ≈ f(p, t + 𝚫t) - f(p, t)
-dx𝚫x + -dy𝚫y ≈ f((x,y), t + 𝚫t) - f((x,y), t)
dx$*$u + dy*v = $I_t$[x,y] - $I_\text{t+△t}$[x,y]

이웃들은 함께
하지만 이런 식으로 근사했을 때, 우리는 두 개의 변수를 모르는데 방정식은 하나 밖에 없다는 문제가 있다. 이 때 "이웃들은 함께 움직인다" 는 루카스-카나데의 핵심 가정이 이용된다. 만약 3X3칸의 픽셀을 이웃으로 잡는다면, 𝚫p를 이루는 $u$, $v$를 구하기 위해 9개의 방정식을 수립할 수 있다. Least squares 방식으로 변위 𝚫p를 구한다.

S = $\begin{bmatrix}dx_1 & dy_1 \\ dx_2 & dy_2 \\ ...&...\end{bmatrix}$ 𝚫p = $(S^\intercal S)^\text{-1}S^\intercal T$

코너를 이용한다
Lukas-Kanade method는 기술적으로는 dense한 알고리즘이지만, feature가 좋지 않은 위 식에서 matrix S가 invertible 하지 않아 해를 구할 수 없게 된다. 따라서 적절한 feature를 가진 포인트를 선택해야 하므로 sparse하게 적용된다. => 이 때, feature로는 코너가 가장 적합하다. 선이라면 해당 선 방향으로의 움직임을 잘 감지하지 못하는 등의 이유인데, 이는 사진에서 적합한 feature로 주로 corner가 선택되는 이유와 같다. 해당 내용은 따로 정리할 것이다.

단점
같은 이미지 내에서 움직임이 있더라도, 빛이 변화하는 경우에 취약하다
큰 움직임에 취약하다
좋은 Feature를 찾을 수 없는 경우 동작하지 않는다
조리개(Aperture) 문제: Lukas-Kanade method의 치명적인 단점은 sparse하다는 점에서 나온다. 특정 영역만을 보면 실제 움직임을 잘못 판별할 수 있기 때문이다. 이발소에 달린 봉은 사실은 옆으로 움직이고 있는데, 특정 부분만을 보면 마치 대각선 위로 움직이고 있는 것처럼 보이는 것을 말한다 (이를 barberpole illusion이라고 한다)

Lucas-Kanade Improved: Iterative Lucas-Kanade

변위를 계산한 뒤, 결과를 이용해 다시 계산을 반복해서 더 나은 계산 결과를 낼 수 있다.

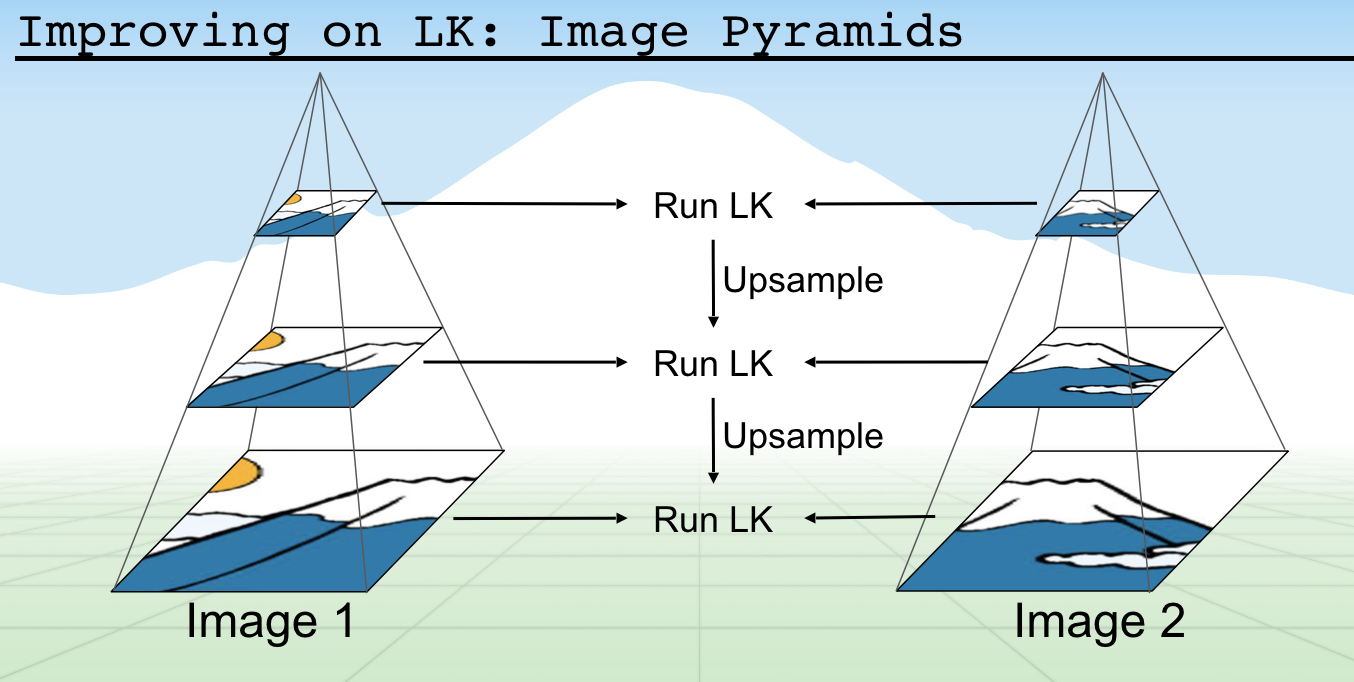
Lucas-Kanade Improved: Pyramidal Lucas-Kanade Method

이미지의 사이즈를 조정하고, 마치 피라미드처럼 쌓아서 이미지의 크기를 작게 하여 계산된 변위 (큰 크기, 대략적) 부터 차례로 LK 알고리즘을 적용해 변위를 계산하는 방식이다. 이런식으로 이미지를 리사이징하고 피라미드 식으로 쌓아 계산하는 방식은 컴퓨터 비전에서 많이 사용되는 트릭이므로 잘 기억해두자!

Dense Optical Flow (Farnebäck Optical Flow)

몇몇 feature에 대해서만 flow를 계산하는 sparse한 방식과는 달리, dense한 방식은 모든 픽셀에 대해서 flow를 계산한다. 이 글에서는 Farnebäck의 알고리즘을 소개한다.
사실 Farnebäck의 알고리즘은 LK 알고리즘과 크게 다르지 않다. Taylor expansion을 할 때 2차항까지 한다는 점이 차이점이기 때문이다. 식을 전개하면 다음과 같다

(p-𝚫p)TAt(p-𝚫p) + bt(p-𝚫p) + ct = pTAt+𝚫tp + bt+𝚫tp + ct+𝚫t
bt+𝚫t = bt - 2At𝚫p
𝚫p = -½(At)-1(bt+𝚫t - bt)
A𝚫p = -½(bt+𝚫t - bt)

이제 LK 알고리즘에서처럼, 이웃들이 함께 움직인다고 가정한 뒤 least squares를 적용하면 변위 𝚫p를 구할 수 있다. 아래 식에서 wi는 Gaussian weight로, 이웃들 중 중앙에 있는 것을 더 많이 고려하기 위해 적용되는 것이다.

$\sum_{i} w_i||A_i \vartriangle p - \vartriangle b_i||^2$

Optical Flow 논문 모음 (end-to-end, SOTA 위주)

end-to-end SOTA 성능을 내는 논문을 모아보았다. 결국 optical flow 계산에는 위에 소개한 방법들이 녹아 있다. 제목을 클릭하면 논문 링크로

1. FlowNet
   Optical Flow를 구하기 위해 최초로 딥러닝 접근법을 도입한 논문이다. 비록 real-world 문제에는 적용하기 어려웠지만, 뛰어난 성능을 보였고 end-to-end라는 점에서 주목받았다

2. FlowNet 2.0
   FlowNet을 연구한 팀에서 기존의 FlowNetC와 FlowNetS를 결합하고, 학습 데이터의 순서를 조정하는 등 조정을 거쳐 정확도를 높인 모델이다. Real-world 자료에도 높은 정확도를 보이지만 모델이 복잡하여 계산 시간이 길기 때문에 real-time 적용은 어렵다. [내가 한 요약]

3. LiteFlowNet
   FlowNet2의 각각의 부분들을 제거하는 등 실험을 통해 모델의 필요 없는 부분을 제거, 같은 효율을 내지만 더 간단한 모형으로 대체하여 동일한 성능을 내지만 가볍고 빠르게 optical flow를 구할 수 있는 모델이다.

4. UnFlowNet
   기존의 딥러닝 접근 방식들은 모두 supervised였는데, 이 논문에서는 unsupervised 방식을 고안했다

5. PWC-Net
   현재 SOTA 모델로, 빠르고 가벼우면서도 최고의 성능을 낸다! 아직 읽어보지는 못했다..

OpenCV 구현

OpenCV 라이브러리에서 두 가지 알고리즘에 대한 모듈을 모두 제공하고 있다. 공식 도큐먼트의 optical flow 게시글에서 영상을 다운로드 받아 하던 것을 내 노트북의 웹캠 영상을 받아 detect 하게끔 바꿔 보았다. Github에 소스 코드를 올려두었다

1. Pyramidal Lukas-Kanade Method 구현

코드

import numpy as np
import cv2 as cv

cap = cv.VideoCapture(0)

# Parameters for ShiTomasi corner detection
feature_params = dict( maxCorners = 100, qualityLevel = 0.3, minDistance = 7, blockSize = 7)

# Parameters for Lucas Kanade optical flow
lk_params = dict( winSize = (15,15), maxLevel = 2, criteria = (cv.TERM_CRITERIA_EPS | cv.TERM_CRITERIA_COUNT, 10, 0.03))

# Create some random colors
color = np.random.randint(0, 255, (100, 3))

# Take first frame and find corners in it
ret, old_frame = cap.read()
old_gray = cv.cvtColor(old_frame, cv.COLOR_BGR2GRAY)
p0 = cv.goodFeaturesToTrack(old_gray, mask=None, **feature_params)

# Create a mask image for drawing purposes
mask = np.zeros_like(old_frame)

while(1):
    ret, frame = cap.read()
    frame_gray = cv.cvtColor(frame, cv.COLOR_BGR2GRAY)

    # Calculate the optical flow with Pyramidal Lucas Kanade
    p1, st, err = cv.calcOpticalFlowPyrLK(old_gray, frame_gray, p0, None, **lk_params)
    # TODO: Select good points
    good_new = p1[st==1]
    good_old = p0[st==1]

    # Draw the tracks
    for i, (new, old) in enumerate (zip(good_new, good_old)):
        a, b = new.ravel()
        c, d = old.ravel()
        mask = cv.line(mask, (a,b), (c,d), color[i].tolist(), 2)
        frame = cv.circle(frame, (a,b), 5, color[i].tolist(), -1)
    img = cv.add(frame, mask)

    cv.imshow('frame', img)
    k = cv.waitKey(30) & 0xff
    if k == 27:
        break
    # Now update the previous frmae and previous points
    old_gray = frame_gray.copy()
    p0 = good_new.reshape(-1, 1, 2)

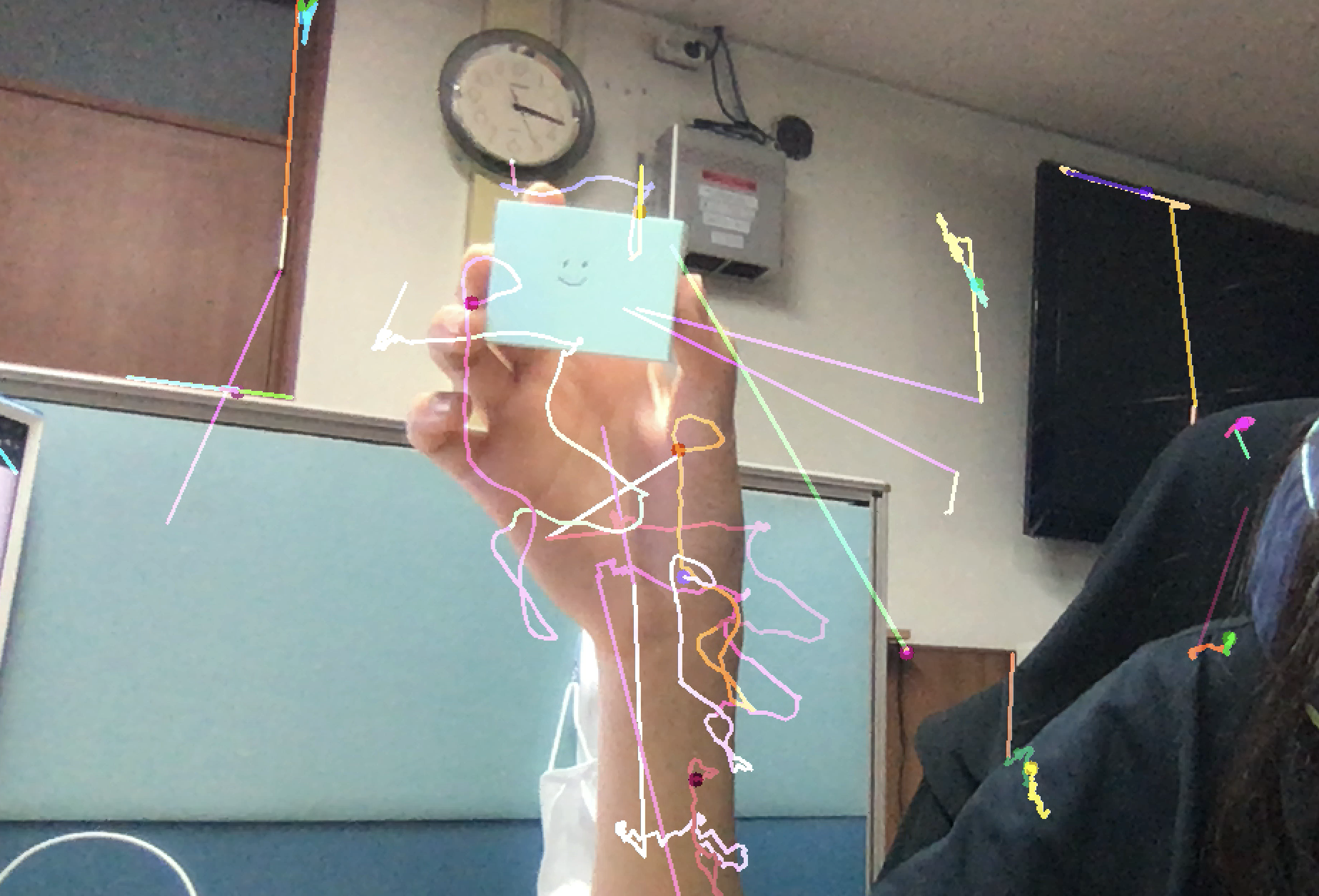
결과
엉망진창 결과물이 완성되었다. 성능이 매우 좋지 않았다. 네모난 물체를 들고 있으면 네모의 끝점이 edge이니 검출이 잘 되지 않을까? 라는 희망을 품어보았지만 어림도 없었다. 파라미터를 조정하거나 corner 탐지하는 알고리즘을 바꿀지 고민이다. 트래킹할 포인트를 맨 처음에 잡고 가는 부분도 수정해봐야겠다.

2. Dense Optical Flow

코드

import numpy as np
import cv2 as cv

cap = cv.VideoCapture(0)
ret, frame1 = cap.read()
prvs = cv.cvtColor(frame1, cv.COLOR_BGR2GRAY)
hsv = np.zeros_like(frame1)
hsv[...,1] = 255
while(1):
    ret, frame2 = cap.read()
    next = cv.cvtColor(frame2, cv.COLOR_BGR2GRAY)
    flow = cv.calcOpticalFlowFarneback(prvs, next, None, 0.5, 3, 15, 3, 5, 1.2, 0)
    mag, ang = cv.cartToPolar(flow[...,0], flow[...,1])
    hsv[...,0] = ang*180/np.pi/2
    hsv[...,2] = cv.normalize(mag, None, 0, 255, cv.NORM_MINMAX)
    bgr = cv.cvtColor(hsv, cv.COLOR_HSV2BGR)
    cv.imshow('frame2', bgr)
    k = cv.waitKey(30) & 0xff
    if k == 27:
        break
    elif k == ord('s'):
        cv.imwrite('opticalfb.png', frame2)
        cv.imwrite('opticalhsv.png', bgr)
    prvs = next 

결과
훨씬 정확하고, 트래킹하는 포인트가 고정된 것이 아니기 때문에 좋은 결과가 나온다. 확실히 속도는 조금 더 느리다.

참고 자료

• Ancient Secret of Computer Vision 강좌 8강
• OpenCV 공식 문서의 Optical Flow 설명