🤔 Swift에는 기본 제공되는 큐가 없다.
앞 글과 같은 이야기를 조금 반복하자면,
BFS(너비 우선 탐색)과 DFS(깊이 우선 탐색)는 트리의 노드를 스캔하는 대표적인 방법이다. 각 방식은 큐와 스택을 이용해 구현하게 되는데, Swift에서 스택은 배열로 구현하면 되지만 큐를 구현하는 것이 문제다. C++처럼 STL로 기본 자료구조들을 제공하고 있지 않기 때문이다... 😢
배열의 메소드 removeFirst()를 쓰면 되지 않느냐 할 수 있지만.. removeFirst()의 시간 복잡도는 무려 O(n)이다! 큐에 쌓여가는 값에 비례해 느려지기 때문에, 코딩테스트에서 일반적으로 사용하기에는 좋지 않다. 그렇다고 큐를 매번 직접 구현해서 쓰기도 힘들다.
그래서 우리는 편법이 필요하다. 큐를 사용하지 않고 값을 넣고 빼는 과정의 시간 복잡도를 최대한 줄이면서도 배열만으로 큐와 같은 효과를 내야 한다. 그렇게 며칠간 고민하고 BFS를 풀며 정리한 편법들을 소개한다. 😏
🗝️ Swift로 BFS를 구현해보자.
총 세 가지 방법을 실제 문제를 풀어보며 살펴보자.
이번에 풀어볼 문제는 백준의 2178 미로탐색 이다.
앞서 BFS를 설명하며 살펴본 문제와 동일한 것으로 N x M 크기의 길(1)과 벽(0)으로 이루어진 미로에서 탈출하는 최단 거리를 구하는 것이 목표이다. 항상 탈출구까지 도착할 수 있는 경우만 입력으로 주어지기 때문에, 탈출 불가 상황은 신경 쓰지 않아도 된다.
방법 1. 배열과 Pointer
큐의 선입 선출 방식대로 배열의 요소를, pointer를 이용해 읽어 들이는 방법이다. 기존 BFS와 달리 값을 계속 배열에 쌓아두는 대신 pointer 값만 바꾸어 현재 탐색 노드를 바꿔가면 된다. 바로 풀이를 보자.
// 문제에서 주어진 미로의 크기 입력 받기.
let NM = readLine()!.split{$0 == " "}.map{Int(String($0))!}
let (N, M) = (NM[0], NM[1])
// 문제에서 주어진 미로 입력 받기.
var map = Array(repeating: [0], count: N)
for i in 0..<N {
map[i] = Array(readLine()!).map{Int(String($0))!}
}
// 문제에서 길은 1, 벽은 0, 탈출구는 N-1, M-1
let wall = 0
let road = 1
// 상하좌우 인접한 칸 탐색을 수월하게 하기위한 상수.
let dr = [1, -1, 0, 0], dc = [0, 0, 1, -1]
// 실제 큐는 아니지만, 의미를 살리기 위해 queue라고 이름지었다.
var queue: [(Int, Int)] = [(0, 0)]
// 배열 queue를 실제 큐처럼 작동하게 만들어줄 pointer 변수.
var pointer = 0
// BFS
// pointer가 queue.count와 같아진다면,
// 원래 BFS에서 큐가 비어 BFS가 끝나는 것과 의미가 동일하다.
while pointer < queue.count {
// 현재 대상 노드. 이 노드의 주변을 탐색할 것이다.
let cur = queue[pointer]
// 앞서 정의한 배열을 통해 간단하게 상하좌우를 탐색한다.
for i in 0..<4 {
// 탐색할 노드의 좌표
let nr = cur.0+dr[i]
let nc = cur.1+dc[i]
// 인덱스 범위를 벗어난 값 처리
if nr>N-1 || nr<0 || nc>M-1 || nc<0 {
continue
}
// map의 값중 road인 것은, 방문한 적이 없으며 벽도 아니라는 것이다.
// 따라서 이동 가능한 길!
if map[nr][nc] == road {
// 방문 표시를 현재 대상 노드 칸의 값 + 1을 해주면
// 자연스럽게 루트로부터의 거리가 된다.
map[nr][nc] = map[cur.0][cur.1] + 1
// 새롭게 방문 가능한 칸이었으므로
// 다음엔 이 칸의 주변을 탐색할 것이므로 큐에 추가한다.
queue.append((nr, nc))
}
}
// 현재 대상 노드의 주변 탐색이 모두 끝났으므로 pointer 값을 하나 올려 준다.
// 이는 큐를 이용한 BFS에서 팝을 해주어 다음 대상 노드로 넘어가는 과정과 같다.
pointer += 1
}
// 탈출 칸의 값은 방문 표시와 겸한 루트로부터의 거리로 채워져 있을 것이므로,
// 탈출 칸의 값을 출력하면 최단거리를 알 수 있다.
print(map[N-1][M-1])참고로, 이 문제는 시작점의 값이 이미 1이기 때문에 방문 표시를 따로 하기가 애매해서 하지 않았다. 그러나 일반적으로 BFS를 사용할 때 시작점에 방문 표시를 하는 걸 까먹으면 큰일난다!
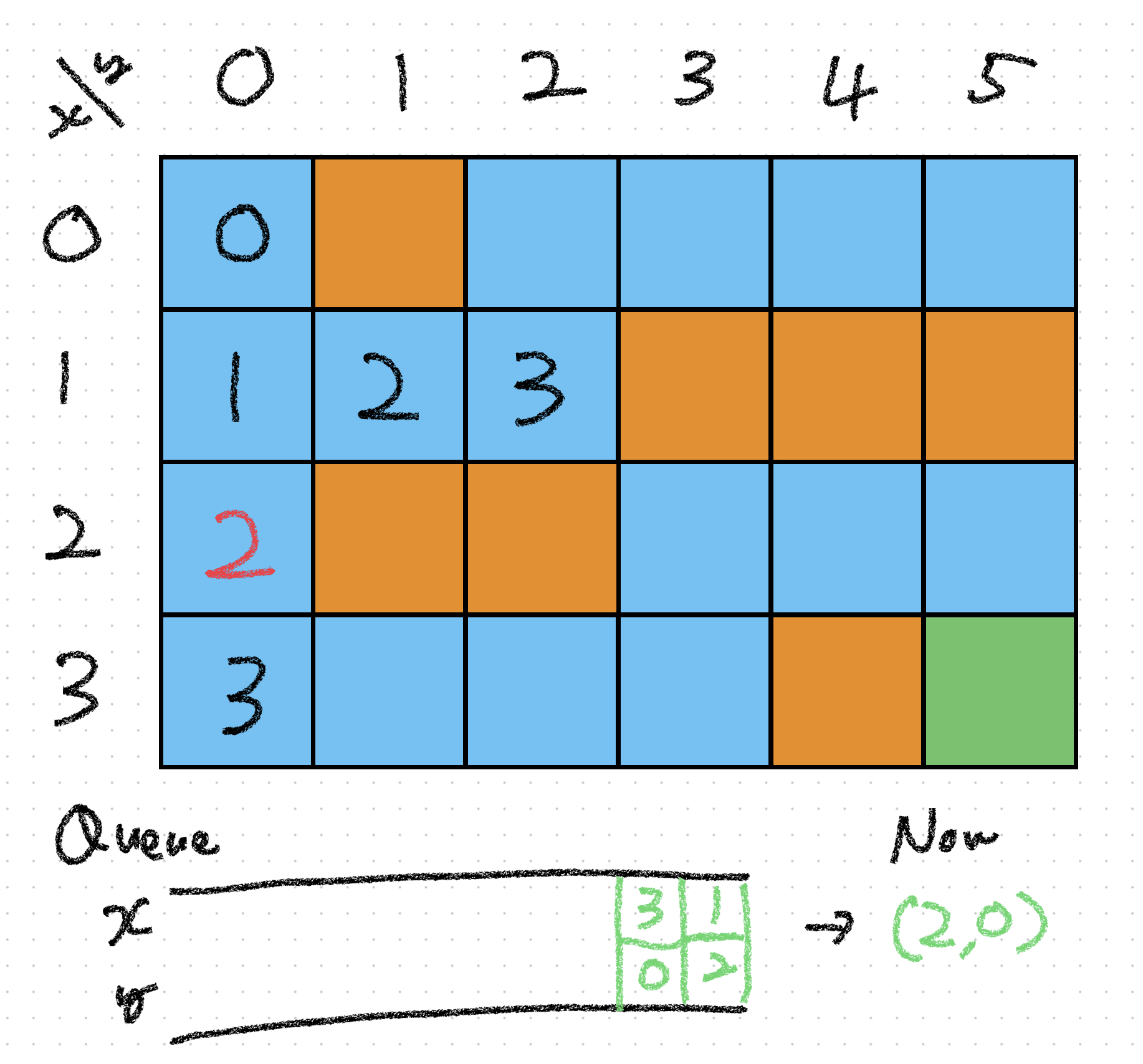
이전 글의 이미지와 큐의 작동 방식을 떠올리며 위 풀이가 배열과 pointer 를 이용해 어떤 식으로 큐를 대체했는지 살펴보자.
위 풀의 배열에는 (시계방향으로 위부터 탐색한다는 가정하에) 이 같은 순서로 값이 채워져 간다.
queue = [(0, 0)]
1번째 루프
pointer = 0, cur = (0, 0)
queue = [(0, 0), (1, 0)]
2번째 루프
pointer = 1, cur = (1, 0)
queue = [(0, 0), (1, 0), (1, 1), (2, 0)]
3번째 루프
pointer = 2, cur = (1, 1)
queue = [(0, 0), (1, 0), (1, 1), (2, 0), (1, 2)]
4번째 루프
pointer = 3, cur = (2, 0)
queue = [(0, 0), (1, 0), (1, 1), (2, 0), (1, 2), (3, 0)]
...
큐는 없지만 새로운 탐색 노드는 뒤에 쌓이고, 현재 대상 노드(cur)은 앞에서부터 하나씩 진행하는 것을 확인할 수 있다. 이처럼 큐 없이 구현할 수 있다!
장단점
장점: 시간 복잡도가 O(N)인 removeFirst()를 사용하지 않고 현재 대상 노드를 배열에서 인덱스로 바로 접근해 꺼내오므로 큐를 이용한 BFS와 같이 시간복잡도를 O(1)로 확보할 수 있다. 구현이 간단하다.
단점: BFS는 동일한 레벨의 노드를 모두 탐색하고, 다음 레벨의 노드로 넘어가는데, 이 계층 탐색의 구조를 잃는다. 정확히 몇 번째 레벨을 탐색하고 있는지 알 수 없다.
(근데 이건 큐를 이용해서 구현한 원래 BFS에서도 같다.)
방법 2. 배열과 2개의 Pointer
이번엔 두 개의 pointer를 이용해 BFS의 계층별로 탐색하는 구조를 살린 풀이다.
let NM = readLine()!.split{$0 == " "}.map{Int(String($0))!}
let (N, M) = (NM[0], NM[1])
var map = Array(repeating: [0], count: N)
for i in 0..<N {
map[i] = Array(readLine()!).map{Int(String($0))!}
}
let wall = 0
let road = 1
let dr = [1, -1, 0, 0], dc = [0, 0, 1, -1]
var queue: [(Int, Int)] = [(0, 0)]
// 배열 queue를 실제 큐처럼 작동하게 만들어줄 pointer 변수
// 이번에 탐색해야 할 계층에 해당하는 queue 내의 칸의 범위를 표현한다.
var startPointer = 0, endPointer = queue.count
// BFS
// 큐에 새로 추가된 칸이 없으면, 두 포인터의 값이 같아지므로 종료하게 된다.
Outer: while startPointer < endPointer {
// 한 계층씩 탐색한다.
searchLevel(startPointer, endPointer)
// 큐 내의 이번 계층에 해당하는 칸의 탐색을 마쳤으므로, 다음 계층으로 넘어간다.
// startPointer는 다음 계층의 첫번째 탐색 노드를, endPointer는 다음 계층의 마지막 탐색점 노드를 가리킨다.
// (정확히는 마지막 탐색 노드의 인덱스 + 1)
startPointer = endPointer
endPointer = queue.count
}
func searchLevel(_ startPointer: Int, _ endPointer: Int) {
for pointer in startPointer..<endPointer {
let cur = queue[pointer]
for i in 0..<4 {
let nr = cur.0+dr[i]
let nc = cur.1+dc[i]
if nr>N-1 || nr<0 || nc>M-1 || nc<0 {
continue
}
if map[nr][nc] == road {
map[nr][nc] = map[cur.0][cur.1] + 1
queue.append((nr, nc))
}
}
}
}
print(map[N-1][M-1])역시 이전 글의 이미지와 큐의 작동 방식을 떠올리며 위 풀이가 배열과 2개의 pointer를 이용해 어떤 식으로 큐를 대체했는지 살펴보자.
queue = [(0, 0)]
1번째 Outer 루프 (루트로부터 거리가 1인 노드 탐색)
startPointer = 0, endPointer = 1
queue = [(0, 0), (1, 0)]
2번째 Outer 루프 (루트로부터 거리가 2인 노드 탐색)
startPointer = 1, endPointer = 2
queue = [(0, 0), (1, 0), (1, 1), (2, 0)]
3번째 Outer 루프 (루트로부터 거리가 3인 노드 탐색)
startPointer = 2, endPointer = 4
queue = [(0, 0), (1, 0), (1, 1), (2, 0), (1, 2), (3, 0)]
4번째 Outer 루프 (루트로부터 거리가 4인 노드 탐색)
startPointer = 4, endPointer = 6
queue = [(0, 0), (1, 0), (1, 1), (2, 0), (1, 2), (3, 0),
(0, 2), (3, 1)]
...
각 Outer 루프 한번마다 거리가 같은 모든 노드를 탐색하는 것을 알 수 있다.
장단점
장점: 앞의 방법과 동일하게 O(1)의 시간 복잡도로 큐와 같이 동작하도록 구현하였다. 계층마다 탐색하고 구분 짓는 것이 중요한 문제라면 이 방법을 통해 풀 수 있다. 한 계층씩 탐색해야 하는 문제는 추후 BFS 응용문제 글에서 다뤄 보겠다!
단점: 음...구현이 복잡한 느낌이다? 시작점이 두 종류인 BFS 문제를 풀 때 주로 한 계층씩 탐색하는 방식으로 구현하게 되는데, 이 방법으로는 구현하는 게 좀 복잡해질 수 있다.
방법 3. 배열을 이용한 계층탐색
queue로 정의한 배열 자체를 계층이 바뀔 때마다 갈아 끼우며 계층 탐색을 할 수 있도록 구현한 것이다. 역시 코드를 보며 생각해 보자.
let NM = readLine()!.split{$0 == " "}.map{Int(String($0))!}
let (N, M) = (NM[0], NM[1])
var map = Array(repeating: [0], count: N)
for i in 0..<N {
map[i] = Array(readLine()!).map{Int(String($0))!}
}
let wall = 0
let road = 1
let dr = [1, -1, 0, 0], dc = [0, 0, 1, -1]
var queue: [(Int, Int)] = [(0, 0)]
var escaped = false
// BFS
while !escaped {
bfs()
if queue.isEmpty {
escaped = true
}
}
func bfs() {
var nextQueue: [(Int, Int)] = []
for cur in queue {
for i in 0..<4 {
let nr = cur.0+dr[i]
let nc = cur.1+dc[i]
if nr>N-1 || nr<0 || nc>M-1 || nc<0 {
continue
}
if map[nr][nc] == road {
map[nr][nc] = map[cur.0][cur.1] + 1
nextQueue.append((nr, nc))
}
}
}
queue = nextQueue
}
print(map[N-1][M-1])역시 이전 글의 이미지와 큐의 작동 방식을 떠올리며 위 풀이가 어떤 식으로 작동하는지 살펴보자.
queue = [(0, 0)]
1번째 루프 (루트로부터 거리가 1인 노드 탐색)
현재까지 탐색한 칸 = [(0, 0), (1, 0)]
queue = [(1, 0)]
2번째 루프 (루트로부터 거리가 2인 노드 탐색)
현재까지 탐색한 칸 = [(0, 0), (1, 0), (1, 1), (2, 0)]
queue = [(1, 1), (2, 0)]
3번째 루프 (루트로부터 거리가 3인 노드 탐색)
현재까지 탐색한 칸 = [(0, 0), (1, 0), (1, 1), (2, 0),
(1, 2), 3, 0)]
queue = [(1, 2), (3, 0)]
4번째 루프 (루트로부터 거리가 4인 노드 탐색)
현재까지 탐색한 칸 = [(0, 0), (1, 0), (1, 1), (2, 0),
(1, 2), (3, 0),(0, 2), (3, 1)]
queue = [(0, 2), (3, 1)]
...
장단점
장점: 역시 동일하게 O(1)의 시간 복잡도로 큐와 같이 동작하도록 구현하였다. 계층마다 탐색하고 구분 짓는 것이 중요한 문제라면 이 방법을 통해 풀 수 있다. 특히, 이 방법은 두 종류의 시작점이 있는 문제에서 각각의 BFS를 구현하기 쉽기 때문에 깔끔하게 풀 수 있다. 추후 BFS 응용문제 글에서 다뤄 보겠다!
단점: -
결론
처음에 BFS 개념을 배우고, 막상 풀어보려 하니 Swift에서는 기본적으로 큐를 제공하지 않아 이러면 도대체 어떻게 해야하는지.. 하는 막막함이 있었다. 그냥 removeFirst()를 쓰는 글도 많았지만, 시간복잡도 면에서 큰 손해이기 때문에 실제로 N이 큰 경우 시간 초과가 나기도 하였다.
그렇게 한동안 고민해 보고 다른 사람의 풀이도 보며 생각해 본 결과, 위 세 가지 방법이 Swift에서 BFS 문제를 푸는 데 그나마 최적의 방법이라고 결론 내렸다. 특히, 마지막 방법은 시작점이 두 종류인 복잡한 BFS 문제를 풀 때 구현이 편해 탁월한 성능을 발휘한다. 다음 글로 BFS의 응용문제 풀이를 작성할 예정이다.
BFS는 자주 나오는 유형인 만큼, 개념을 바탕으로 이러한 틀 자체를 익혀두고 빠르게 작성할 수 있는 정도로 연습해 두자.
Swift로 된 자료들이 많이 부족한 만큼, 이 글이 Swift로 알고리즘 문제를 푸는 사람들에게 도움이 되길 바란다.
참고
여러 사람의 풀이와 나의 문제 풀이 경험