1. LSTM과 GRU 개발 배경

SimpleRNN은 이론적으로 시간 t에서 이전의 모든 타임스텝의 정보를 유지할 수 있다. 실제로 긴 시간에 걸친 의존성은 학습할 수 없는 것이 문제이다. 층이 많은 Feedforward Network에서 나타나는 것과 비슷한 현상인 기울기 소실 문제(Vanishing Gradient Problem)때문이다. Feedforward Networt에 층을 많이 추가할수록 훈련하기 어려운 것과 같다.

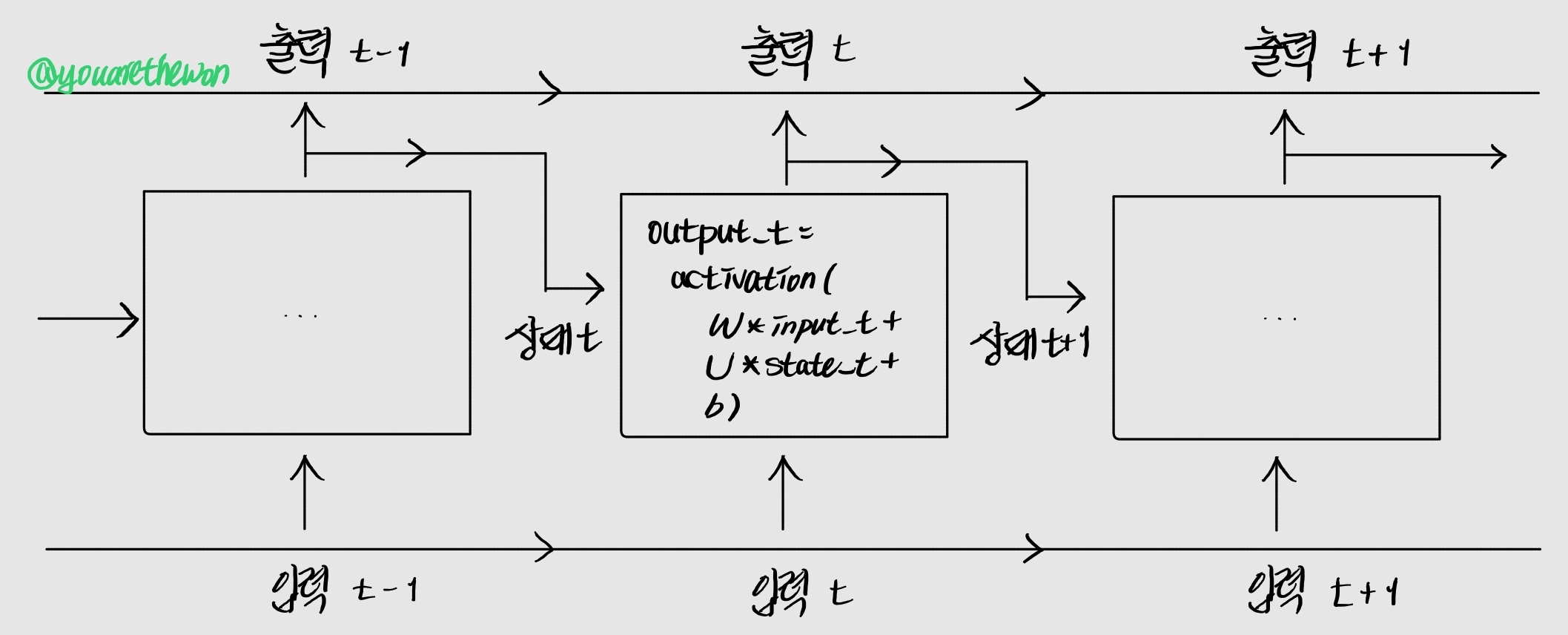
순환 신경망의 역전파는 위 그림과 같이 타임스텝에 따라 네트워크가 펼쳐진 것처럼 진행된다. 이를 BPTT(BackPropagation Through Time)라고 한다. 역전파가 진행되는 동안 타임스텝마다 동일한 가중치를 사용하기 때문에 타임스텝이 길어질수록 기울기 값이 급격히 줄어들거나(Vanishing Gradient Problem) 급격히 증가할 수 있다(Exploding Gradient Problem).

기울기 소실 문제를 해결하기 위해 고안된 것이 LSTM과 GRU 층이다.

2. LSTM

LSTM(Long Short-Term Memory, 장단기 메모리) 알고리즘은 기울기 소실 문제에 대한 연구의 결정체이다. LSTM 층은 SimpleRNN의 한 변종으로 정보를 여러 타임스텝에 걸쳐 나르는 방법이 추가된다. 나중을 위해 정보를 저장함으로써 처리 과정에서 오래된 시그널이 점차 소실되는 것을 막아준다. 이를 자세하게 이해하기 위해 다시 아래 SimpleRNN 셀을 살펴보자.

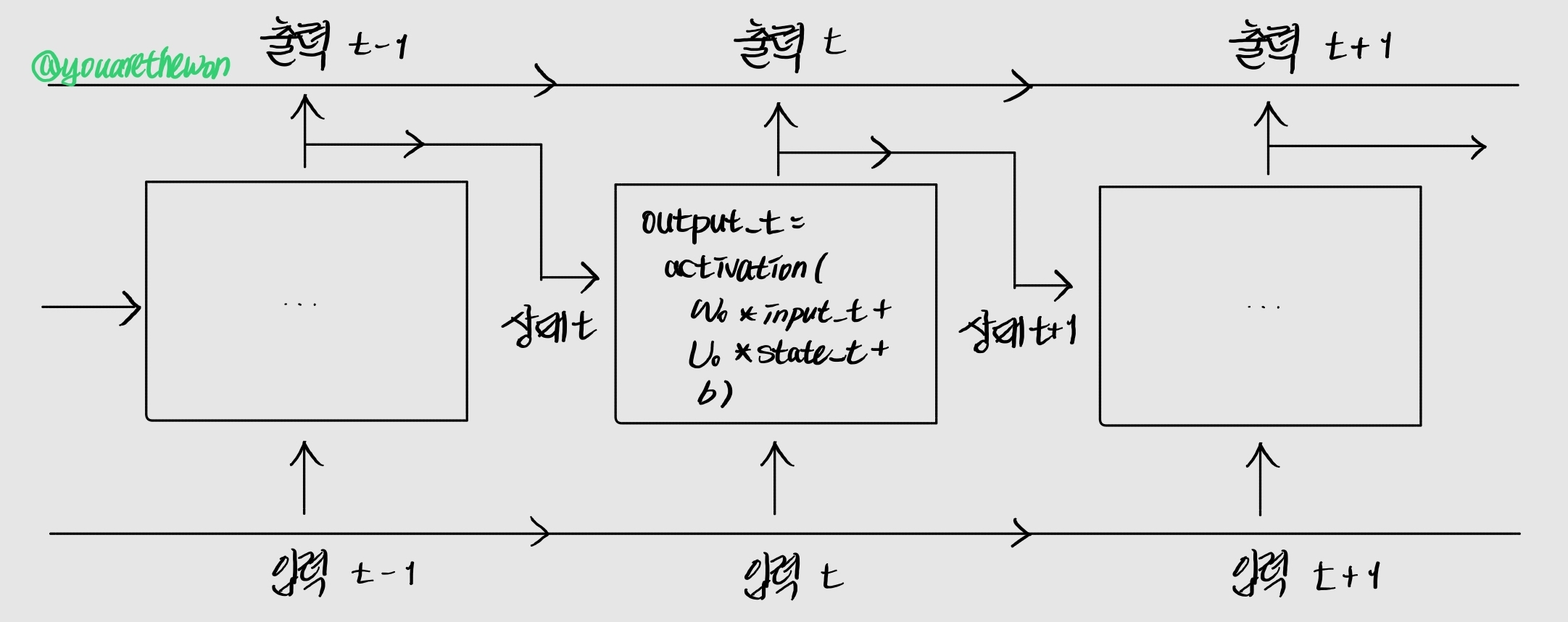
가중치 행렬 여러 개가 나오므로 출력(output)을 나타내는 문자 o로 셀에 있는 W와 U 행렬을 표현하겠다(Wo, Uo).
이 그림에 타임스텝을 가로질러 정보를 나르는 데이터 흐름을 추가해보자. 타임스텝 t에서 이 값을 이동 상태 c_t라고 부르겠다. 여기서 c는 이동(carry)을 의미한다. 이 정보를 사용하여 셀이 다음과 같이 바뀐다.

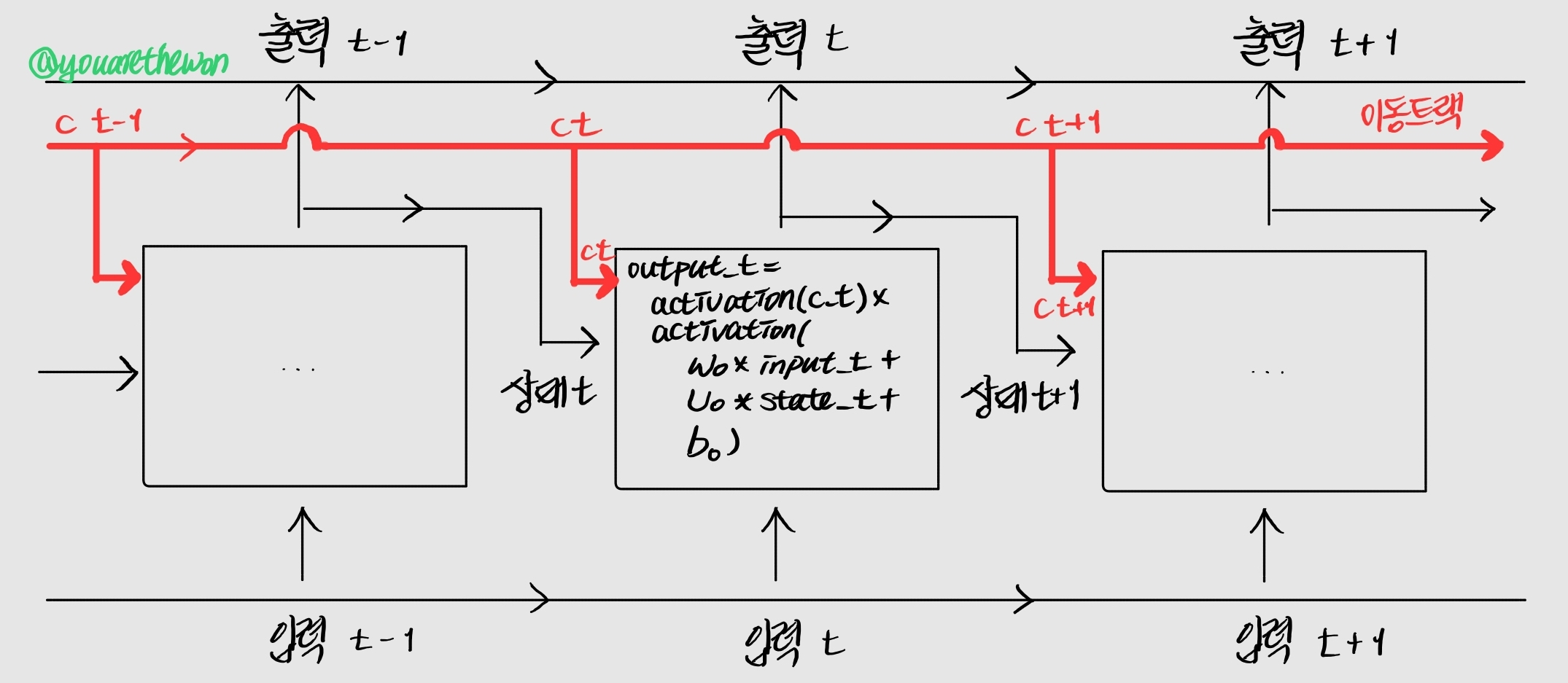
입력 연결과 순환 연결(상태)로부터 이 정보가 합성된다. 그러고는 다음 타임스텝으로 전달될 상태를 활성화 함수와 곱셈(activation(c_t) x)을 통해 변경시킨다. 개념적으로 보면 데이터를 실어 나르는 이 흐름이 다음 출력과 상태를 조절한다.

이제 복잡한 부분은 데이터 흐름에서 다음 이동 상태(c_t+1)가 계산되는 방식이다. 여기에는 3개의 다른 변환이 관련되어 있다. 3개 모두 SimpleRNN과 같은 형태를 가진다.

y = activation(dot(state_t, U) + dot(input_t, W) + b)

3개의 변환 모두 자신만의 가중치 행렬을 가진다. 각각 i, f, k로 표시하겠다. 다음이 지금까지 설명한 내용이다.

# LSTM pseudocode 1
output_t = activation(c_t) * activation(dot(input_t, Wo) + dot(state_t, Uo) + bo)

i_t = activation(dot(state_t, Ui) + dot(input_t,Wi) + bi)
f_t = activation(dot(state_t, Uf) + dot(input_t, Wf) + bf)
k_t = activation(dot(state_t, Uk) + dot(input_t, Wk) + bk)

i_t, f_t, k_t를 결합하여 새로운 이동 상태(c_t+1)를 구한다.

c_t+1 = i_t * k_t + c_t * f_t

그림으로 나타내면 다음과 같다.

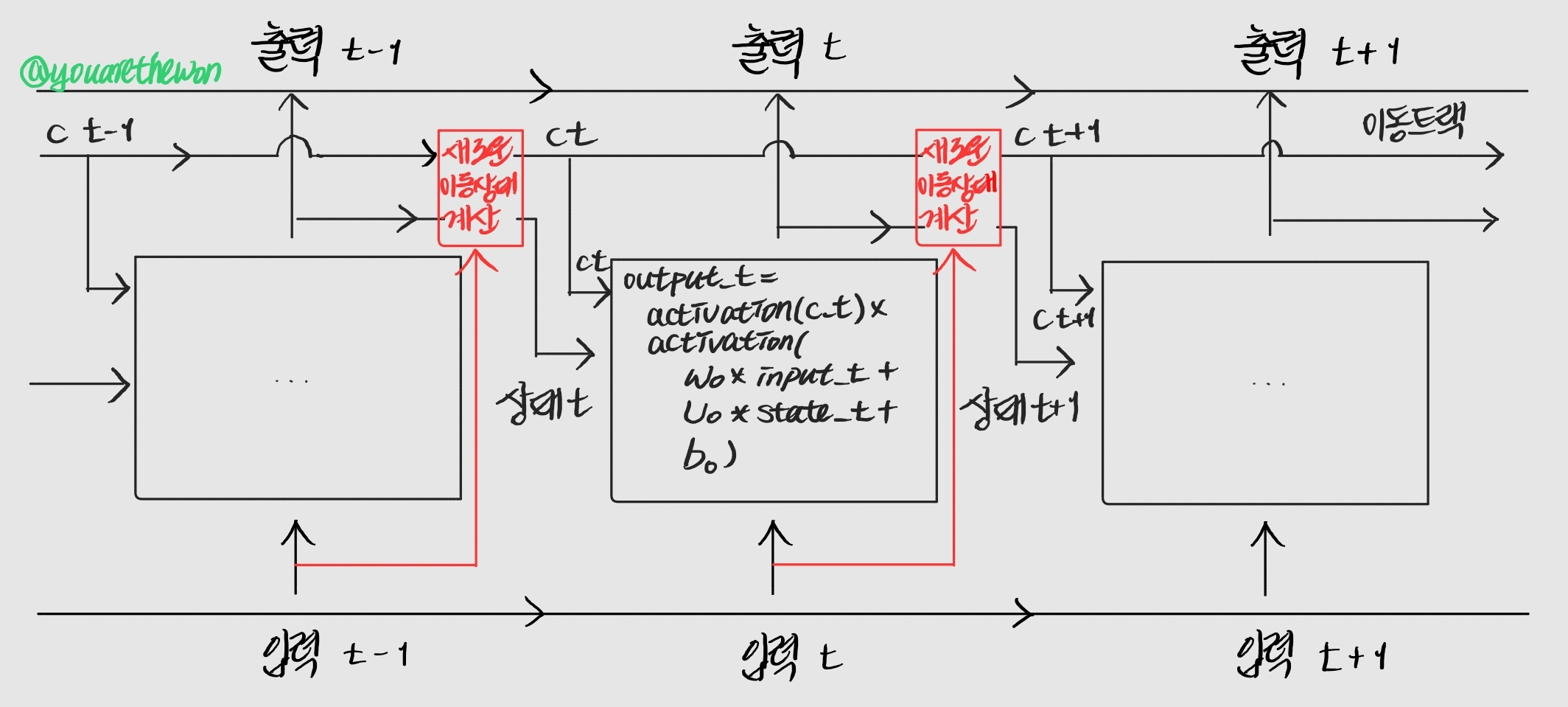
c_t와 f_t의 곱셈은 이동을 위한 데이터 흐름에서 관련이 적은 정보를 의도적으로 삭제한다고 볼 수 있다. 한편 i_t와 k_t는 현재에 대한 정보를 제공하고 이동 트랙을 새로운 정보로 업데이터한다. 하지만 이런 해석은 큰 의미가 없다. 이 연산들이 실제로 하는 일은 연산에 관련된 가중치 행렬에 따라 결정되기 때문이다. 이 가중치는 end-to-end 방식으로 학습된다. 이 과정은 훈련 반복마다 매번 새로 시작되며 이런저런 연산들에 특정 목적을 부여하기가 불가능하다. RNN 셀의 사양(specification)은 가설 공간을 결정한다. 훈련할 때 이 공간에서 좋은 모델 파라미터를 찾는다. 셀의 사양이 셀이 하는 일을 결정하지 않는다. 이는 셀의 가중치에 달려 있다. 같은 셀이더라도 다른 가중치를 가지는 경우 매우 다른 작업을 수행해야 한다. 따라서 RNN 셀을 구성하는 연산 조합은 엔지니어링적 설계가 아니라 가설 공간의 제약 조건으로 해석하는 것이 낫다.

3. 정리

SimpleRNN은 과거의 정보를 저장할 수 있지만 기울기 소실 문제가 발생한다. 이를 해결하기 위해 LSTM과 GRU가 개발되었다.

LSTM은 SimpleRNN의 한 변종으로 정보를 여러 타임스텝에 걸쳐 나르는 방법이 추가된다. 이를 통해 머나먼 과거의 정보를 잃게 되는, 즉 기울기 소실 문제를 해결할 수 있다.

다음 포스팅에서는 LSTM layer를 사용한 모델을 구성해보겠다.