1. 순환 신경망이란?

Fully Connected Network나 Convolutional Neural Network같은 신경망의 특징은 메모리가 없다는 것이다. 네트워크에 주입되는 입력은 개별적으로 처리되며 입력 간에 유지되는 상태가 없다. 이런 네트워크로 시퀀스나 시계열 데이터 포인트를 처리하려면 네트워크에 전체 시퀀스를 주입해야 한다. 즉 전체 시퀀스를 하나의 데이터 포인트로 변환해야 한다. 예를 들어 이전에 작성한 IMDB 문제에서 영화 리뷰 하나를 큰 벡터 하나로 변환하여 처리하였다. 이런 네트워크를 feedforward network라고 한다.

이와 반대로 사람이 문장을 읽는 것처럼 이전에 나온 것을 기억하면서 단어별로 또는 한눈에 들어오는 만큼씩 처리할 수 있다. 이는 문장에 있는 의미를 자연스럽게 표현하도록 도와준다. 생물학적 지능은 정보 처리를 위한 내부 모델을 유지하면서 점진적으로 정보를 처리한다. 이 모델은 과거 정보를 사용하여 구축되며 새롭게 얻은 정보를 계속 업데이트한다.

비록 극단적으로 단순화시킨 버전이지만 순환 신경망(Recurrent Neural Network, RNN)은 같은 원리를 적용한 것이다. 시퀀스의 원소를 순회하면서 지금까지 처리한 정보를 상태(state)에 저장한다. 사실 RNN은 내부에 루프(loop)를 가진 신경망의 한 종류이다. RNN의 상태는 2개의 다른 시퀀스(2개의 다른 IMDB 리뷰)를 처리하는 사이에 재설정된다. 하나의 시퀀스가 여전히 하나의 데이터 포인트로 간주된다. 즉 네트워크에 하나의 입력을 주입한다고 가정한다. 이 데이터 포인트가 한 번에 처리되지 않는다는 것이 다르다. 그 대신 네트워크는 시퀀스의 원소를 차례대로 방문한다.

2. RNN 원리를 바탕으로 구현해보기

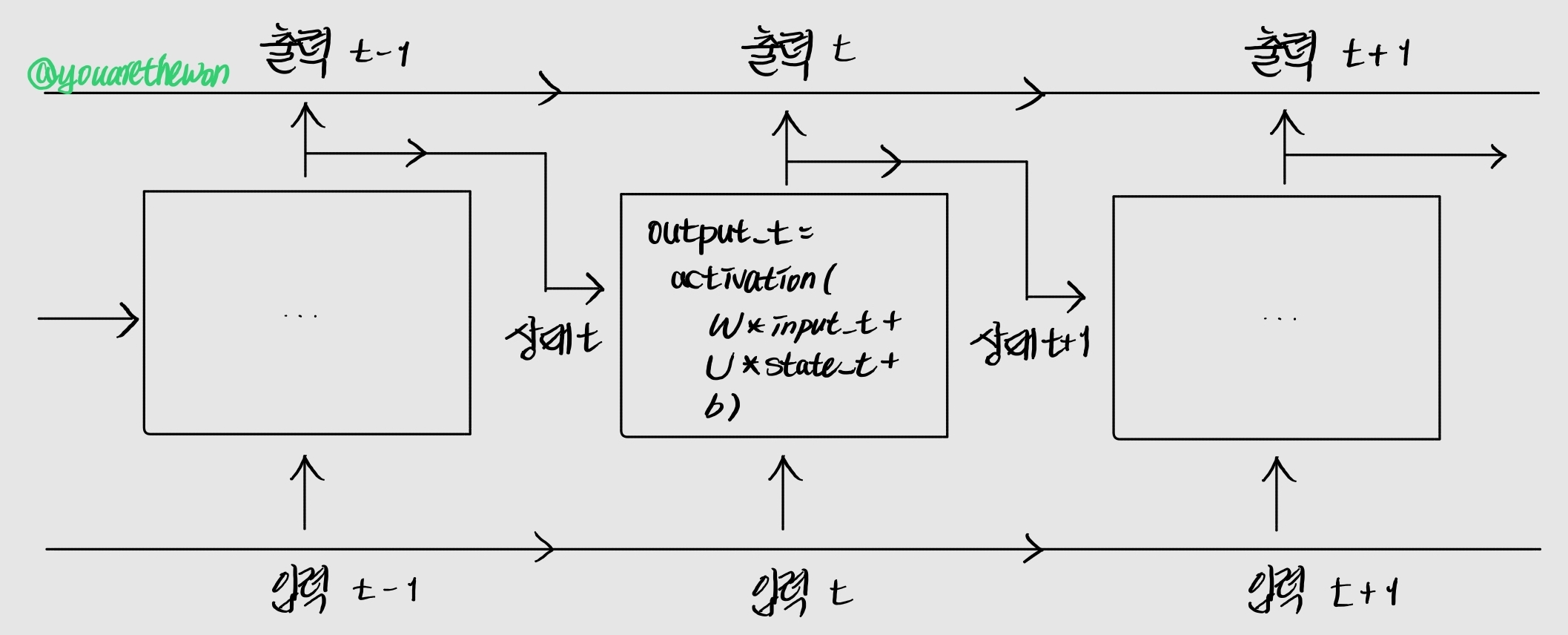
루프와 상태에 대한 개념을 명확히 하기 위해 Numpy로 간단한 RNN 정방향 계산을 구현해보겠다. 이 RNN은 크기가 (timesteps, input_features)인 2D 텐서로 인코딩된 벡터의 시퀀스를 입력받는다. 이 시퀀스는 타임스텝을 따라서 반복된다. 각 타임스텝 t에서 현재 상태와 ((input_features,) 크기의) 입력을 연결하여 출력을 계산한다. 그 다음 이 출력을 다음 스텝의 상태로 설정한다. 첫 번째 타임스텝에서는 이전 출력이 정의되지 않으므로 현재 상태가 없다. 이때는 네트워크의 초기 상태(initial state)인 0 벡터로 상태를 초기화한다.
pseudocode로 표현하면 RNN은 다음과 같다.

# 간단한 pseudocode로 표현한 RNN

state_t = 0 # 상태, 이전 단계의 출력 값
for input_t in input_sequence:
    output_t = f(input_t, state_t) # 이전 단계의 출력 값과 현재 단계의 input을 결합하여 연산
    state_t = output_t             # 연산 결과는 다음 단계에서 이전 단계의 출력 값 역할

f 함수는 입력과 상태를 출력으로 변환한다. 이를 2개의 행렬 W와 U 그리고 편향 벡터를 사용하는 변환으로 바꿀 수 있다. 피드포워드 네트워크의 완전 연결 층에서 수행되는 변환과 비슷하다.

# 더 자세한 pseudocode로 표현한 RNN

state_t = 0 # 상태, 이전 단계의 출력 값
for input_t in input_sequence:
     # W와 입력 벡터 간 행렬곱, U와 이전 단계의 은닉 상태 간 행렬곱, 편향 벡터를 활성화 함수에 입력하여 출력 값 계산
    output_t = activation(dot(W, input_t) + dot(U, state_t) + b)
    state_t = output_t

완벽하게 설명하기 위해 간단한 RNN의 정방향 계산을 Numpy로 구현해보겠다.

# Numpy로 구현한 간단한 RNN

import numpy as np

timesteps = 100 # 입력 시퀀스에 있는 타임 스텝의 수
input_features = 32 # 입력 특성의 차원
output_features = 64 # 출력 특성의 차원

inputs = np.random.random((timesteps, input_features)) # 입력 데이터, (timesteps, input_features)인 2D 텐서로 인코딩된 벡터
state_t = np.zeros((output_features,))                 # 초기 상태, 모두 0인 벡터
print(f"inputs shape: {inputs.shape}")

# 랜덤한 가중치 행렬
W = np.random.random((output_features, input_features))
U = np.random.random((output_features, output_features))
b = np.random.random((output_features,))

print(f"W shape: {W.shape}")
print(f"input_t shape: {inputs[0].shape}")
print(f"W x input_t: {np.dot(W, inputs[0]).shape}\n")
print(f"U shape: {U.shape}")
print(f"state_t shape: {state_t.shape}")
print(f"U x state_t: {np.dot(U, state_t).shape}\n")
print(f"b shape: {b.shape}\n")

successive_outputs = []
for idx, input_t in enumerate(inputs):
    output_t = np.tanh(np.dot(W, input_t) + np.dot(U, state_t) + b) # 입력과 이전의 출력을 연결하여 현재 출력 계산
    successive_outputs.append(output_t)                             # 현재 출력 값 저장
    if (idx <= 5) | (idx >= 95):
        print(f"{idx}번째 은닉층 출력: {output_t.shape}")
    if (idx == 50):
        print("...\n")
    state_t = output_t                                              # 다음 타임스텝을 위해 네트워크 상태 업데이트

final_output_sequence = np.stack(successive_outputs, axis=0) # 최종 출력은 크기가 (timesteps, output_features)인 2D 텐서
print(f"최종 출력: {final_output_sequence.shape}")

요약하면 RNN은 반복할 때 이전에 계산한 정보를 재사용하는 for 루프에 지나지 않는다. 물론 이 정의에 맞는 RNN의 종류는 많다. 위 예시는 가장 간단한 RNN의 형태이다.
RNN은 스텝(step) 함수에 의해 특화된다. 위 예시에서는 다음과 같다.

output_t = np.tanh(np.dot(W, input_t) + np.dot(U, state_t) + b)