[백준] 11053번: 가장 긴 증가하는 부분 수열

Kim Yuhyeon·2022년 3월 15일

C 백준 알고리즘

알고리즘 + 자료구조

목록 보기

19/161

https://www.acmicpc.net/problem/11053

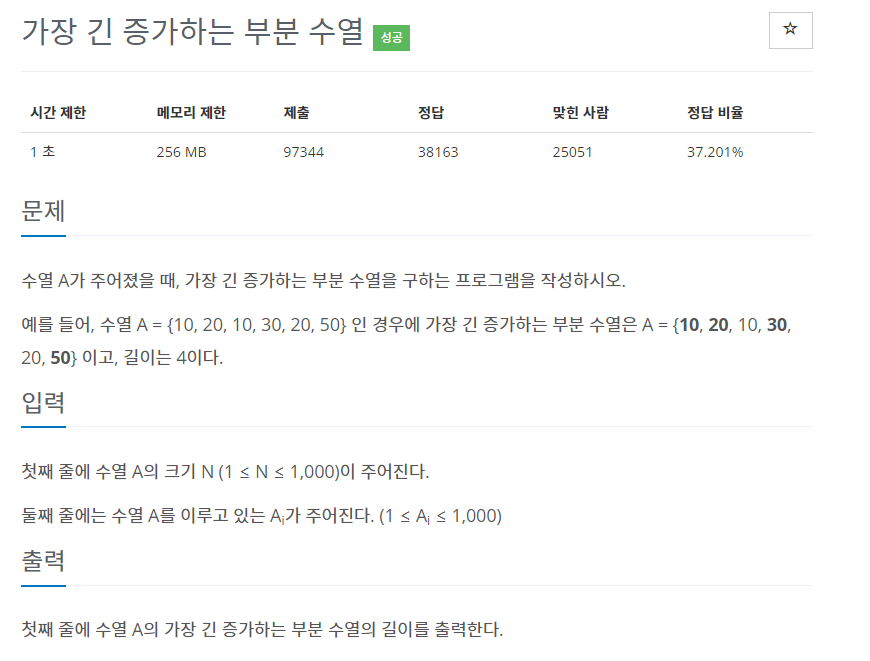
문제

예제

6
10 20 10 30 20 50

>> 4

20
322 831 212 232 545 698 260 265 324 215 701 75 156 605 851 993 425 887 691 593

>> 8

알고리즘 접근 방법

DP를 이용한다.

수열 Ai와 가장 긴 증가하는 부분 수열의 길이를 저장하는 배열 dp가 있다.

N번째 길이에서 찾을 수 있는 가장 긴 부분 수열은

자기 자신보다 작은 수들 각각의 부분 수열 중 제일 큰 부분 수열 + 1 이다.

예를 들어 예제 수열을 보면
[ 10 20 10 30 20 50 ]
dp는 참고로 모두 1로 초기화 해준다. (제일 짧은 부분 수열의 길이)

N=1
dp[1] = 1
N=2
1번째 수가 2번째 수보다 작기 때문에 (10 < 20)
dp[2] = max(1, dp[1]+1) = max(1, 1+1) = 2
N=3
3번째 수 10은 자기 자신 보다 작은 수가 없어 증가하는 부분 수열이 없기 때문에 그대로 1이다.
N=4
4번째 수 30은 자기 자신보다 작은 수가 모두 있다.
이 때 Ai와 dp를 비교하면
Ai : 10, 20, 10
dp : 1 , 2 , 1

따라서 dp[4] = 자기 자신보다 작은 수의 dp들 값 중 제일 큰 dp + 1 = dp[2]+1 = 3

이런식으로 나아가다보면 dp[N] =
1. Ai[1~N-1]번째 값 중 Ai[N]보다 더 작은 숫자들 = i라고 할 때
2. 이들이 갖는 dp[i]에서 제일 큰 값을 찾고 +1 한다.

풀이

#include <iostream>

using namespace std;

int main(){

    int A;
    cin >> A;
    int Ai[A+1] = {0,}; 

    for(int i=1; i<=A; i++)
        cin >> Ai[i];


    long long dp[A+1] = {1, }; // 증가하는 수열의 길이를 저장 (1보다 작을 수 없으므로 1로 초기화)

    // 초기식 
    dp[1] = 1;   

    for(int i=2; i<=A; i++){
        dp[i] = 1;
        for(int j=1; j<i; j++){
            if(Ai[j] < Ai[i]){ // 현재 값보다 작다면    
                dp[i] = max(dp[j]+1, dp[i]); // 작은 값들 중에 부분 수열 + 1 을 계속 갱신한다.
            }
        }
    }
    int result = 0;
    for (int i=1; i<=A; i++){
        if (dp[i] > result)
            result = dp[i];
    }
    cout << result << endl;

}