4장 가장 훌륭한 예측선
딥 러닝의 가장 말단에서 이루어지는 기본적인 두 가지 계산 원리
선형회귀 , 로지스틱회귀
가장 훌륭한 예측선 = 선형 회귀 분석을 이용한 모델
1. 선형 회귀의 정의
딥 러닝에는 정보가 필요하다!
ex) 성적을 변하게 만드는 정보
성적을 변하게 만드는 '정보' 요소를 x라고 하고, 변하는 성적을 y라고 함.
==> x값이 변함에 따라 y값이 변한다.
x를 독립변수라고 하고 x에 따라 움직이는 y를 종속변수라고 합니다.
선형 회귀 란
독립 변수 x를 사용해 종속 변수 y의 움직임을 예측하고 설명하는 작업
x1, x2, x3등으로 여러 값으로 설명도 가능
하나의 x값으로 y값을 설명 할 수있다면 단순 선형 회귀 라고도 함.
x가 여러개 필요하다면 다중 선형 회귀
2. 가장 훌륭한 예측선
y = ax + b
지금 주어진 데이터에서 선형 회귀는 최적의 a, b 값을 찾아내는 작업
a,b를 찾는다면 지금 주어진 조건에서 x에 값을 대입하고 다음 x로 결과를 예측할수 있음
3. 최소 제곱법
최소 제곱법
y= ax + b일때
a = (x-x의 평균)(y-y의 평균)의 합 / (x-x의 평균)^2의 합
*b - y의 평균 -(x의 평균 기울기 a)
y의 평균에서 x의 평균과 기울기의 곱을 빼면 b값이 나온다는 의미
ex) 이렇게 구한 식이 y = 2.3x + 79
x를 대입하면 나오는 y의 값을 '예측 값'이라고 합니다.
4. 파이썬 코딩으로 확인하는 최소 제곱
import numpy as np
#공부한 시간과 점수를 각각 x,y라는 이름의 넘파이 배열로 만든다
x = np.array([2,4,6,8])
y= np.array([81, 93, 91, 97])
mx = np.mean(x) # 원소의 평균을 구하는 넘파이 함수는 mean()이다.
my = np.mean(y)
print("x의 평균 값 ", mx)
print("y의 평균 값 ", my)
#파이썬 명령을 만들 차례
divisor = sum([(i -mx)**2 for i in x])
#sum은 시그마 , **2는 제곱을 구하라는 의미, for i in x는 x의 각 원소에 i자리에 대입하라는 의미
#임의의 변수 d의 초깃값을 0으로 설정하고 x의 개수만큼 실행 ==> 최소 제곱법을 구현
def top(x, mx, y, my):
d = 0
for i in range(len(x)):
d += (x[i] - mx) * (y[i] - my)
return d
dividend = top(x, mx, y, my)
print("분모 ", divisor)
print("분자 :", dividend)
a = dividend / divisor
b = my -(mx* a)
print("기울기 a = " , a)
print("y 절편 b", b)
결과
x의 평균 값 5.0
y의 평균 값 90.5
분모 20.0
분자 : 28.5
기울기 a = 1.425
y 절편 b 83.375
왜 이렇게 나왔는지 모르겠다 ㅠ
5. 평균 제곱 오차
x의 데이터 , 즉 변수가 증가하는 경우에는 어떻게 할 것인가? = "조금씩 수정해 나가는 방식"
오차를 구할 때 가장 많이 사용하는 방식 평균 제곱 오차
그래프에서 a, b의 값이 바뀔 때 생기는 오차의 합이 작으면 좋다!
오차를 구하는 방정식
오차 = 실제 값 - 예측 값
주의사항은 오차의 합을 구할 때에는 오차의 값을 제곱해서 부호를 없앤다.
오차의 합 = 시그마 i=0부터 n까지 (yi-yi예측값)^2
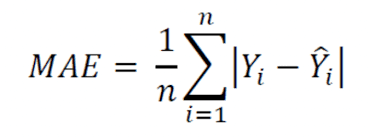
이 식은 아주 중요함!!
절대 값은 제곱으로 해결
선형 회귀란 임의의 직선을 그어 이에 대한 평균 제곱 오차를 구하고, 이 값을 가장 작게 만드는 a, b의 값을 찾아가는 방식
6. 파이썬 코딩으로 확인하는 평균 제곱오차
가상의 기울기, 가상의 절편을 구현한다.
import numpy as np
#가상의 기울기 a, b를 정한다.
fake_a = 3
fake_b = 76
#공부한 시간과 점수를 각각 x,y라는 이름의 넘파이 배열로 만든다
x = np.array([2,4,6,8])
y= np.array([81, 93, 91, 97])
def predict(x):
return fake_a * x + fake_b
predict_result = []
for i in range(len(x)):
predict_result.append(predict(x[i]))
print("공부시간 =%.f, 실제점수 =%f, 예측점수=%.f" % (x[i], y[i], predict(x[i])))
n = len(x)
def mse(y,y_pred):
return(1/n)*sum((y - y_pred)**2)
print("평균 제곱 오차:" + str(mse(y,predict_result)))
결과
공부시간 =2, 실제점수 =81.000000, 예측점수=82
공부시간 =4, 실제점수 =93.000000, 예측점수=88
공부시간 =6, 실제점수 =91.000000, 예측점수=94
공부시간 =8, 실제점수 =97.000000, 예측점수=100
평균 제곱 오차:11.0
