9장 오차 역전파에서 딥러닝으로

오차 역전파의 등장으로 은닉층에 포함된 가중치를 업데이트 할 수 있게 되었습니다. --> 우리가 아는 딥러닝의 탄생으로 이어짐.

1. 딥러닝의 태동, 오차 역전파

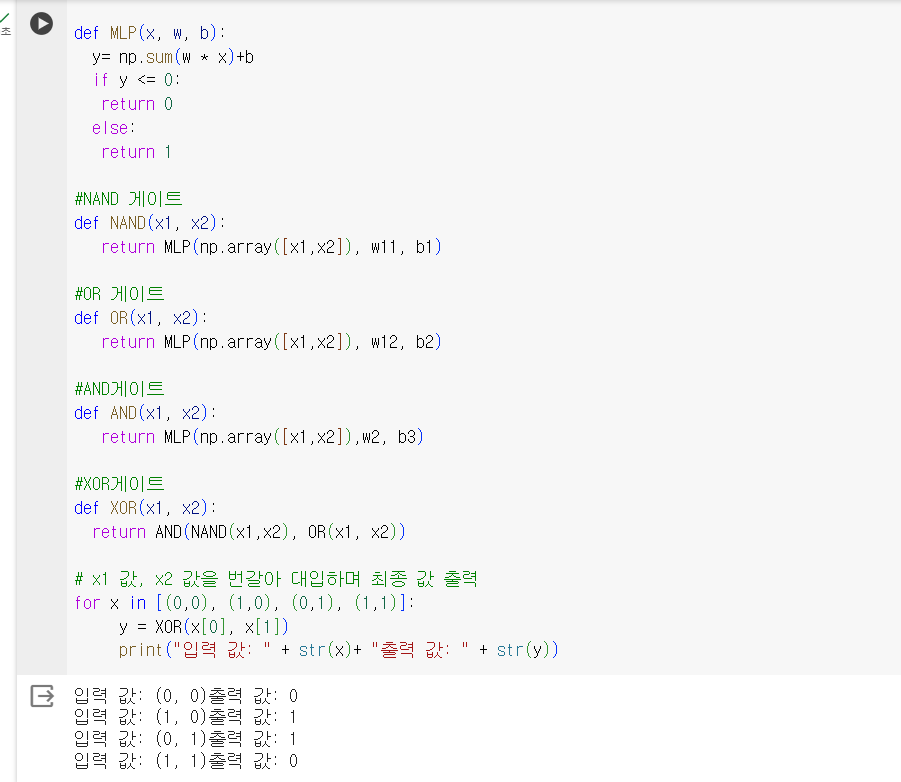
앞서 XOR문제를 해결했지만, 입력 값과 출력 값을 알고 있는 상태에서 가중치(w)와 바이어스(b)를 미리 알아본 후 이를 집어넣었습니다.

우리가 원하는 것은 데이터를 통해 스스로의 가중치를 조절하는 '학습'의 실입니다.

오차 역전법은 어떻게 가중지를 업데이트 할까?
이를 설명하기 위해 다시 경사 하강법이야기로 돌아가자

경사 하강법은 임시의 가중치를 선언하고 결괏값을 이용해 오차를 구한 후
이 오차가 최소인 지점으로 계속해서 조금씩 이동시키는 것이었습니다.
이 오차가 최소인 지점은 미분했을 때 기울기가 0이 되는 지점이라고 했었습니다.

하지만 이 경사하강법은 '단일 퍼셉트론', 즉 입력값과 출력층만 존재할때 가능한 이야기입니다. 은닉층이 생기면 우리는 두 번의 경사하강법을 실행해야 합니다. 즉 가중치를 한 번 수정하고, 그림처럼 가중치를 두 번 수정해야 하는 것 입니다.

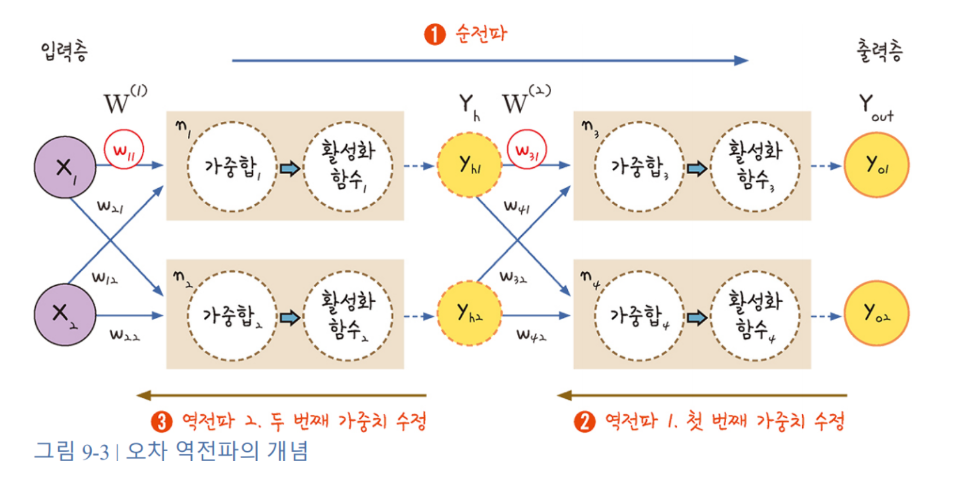
1처럼 한 번 순전파가 일어나고 이 과정을 통해 각 가중치의 초깃값이 정해집니다. 초깃값의 가중치로 만들어진 값과 실제 값을 비교해 출력층의 오차를 계산합니다. 목표는 이때 계산된 출력층의 오차를 최소화 시키는 것입니다.

2번 첫번째 가중치를 수정하는 과정과 3번 두번째 가중치를 수장하는 과정이 필요합니다.

ex) w31를 업데이트 하기 위해서는 w31에 대해 편미분해야하고 합성함수의 미분을 이용해서 체인 룰을 적용해 편미분을 구하고 업데이트

w11의 경우에는 y01과 y02가 모두 관여되어있으므로 오차 2개를 모두 계산해 편미분을 해야합니다.

첫 번째 가중치 업데이트 공식 = (y01 - y실제값) y01(1-y01) yh1

두 번째 가중치 업데이트 공식
= (시그마 y01 w31 + 시그마 y02 w41)yh1(1-yh1)x1

2.기울기 소실 문제와 활성화 함수

은닉층이 깊어질 경우, 출력층에서 시작된 가중치의 업데이트가 처음 층까지 업데이트가 되지 않는 현상이 발생하게 됩니다. 이는 활성화 함수로 사용된 시그모이드 함수의 특성 때문입니다.

시그모이드 함수의 최대치는 0.25이므로 계속해서 시그모이드 함수를 곱하면 0에 수렴하는 결과가 생깁니다.

렐루 함수 라는 새로운 개념의 도입

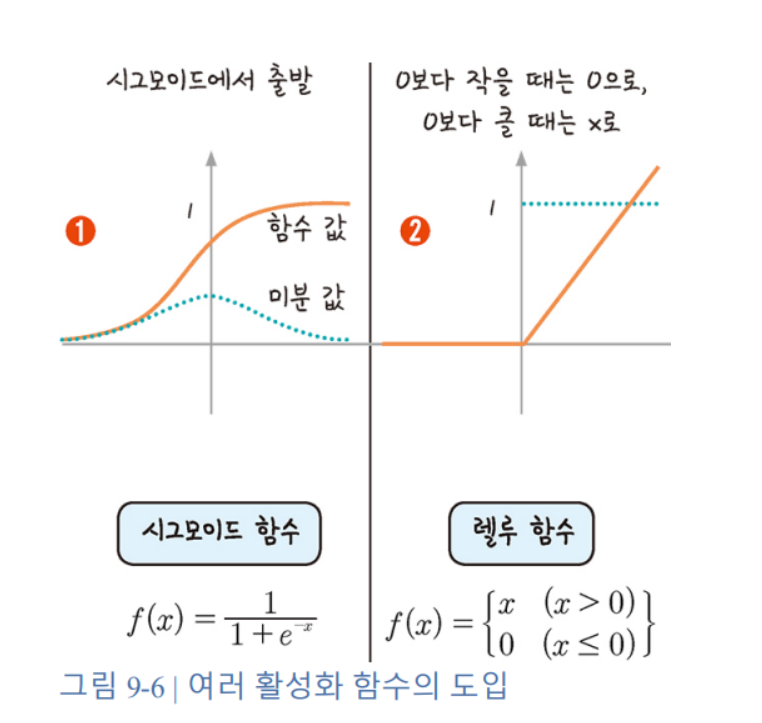
x가 0보다 작을 때 모든 값을 0으로 처리하고, 0보다 큰 겂은 x를 그대로 사용하는 방법.

-->렐루 함수를 사용하면 오차 역전파가 진행되어도 맨 처음 층까지 값이 남아 있게 됩니다.

외에도 활성화 함수에는 하이퍼볼릭 탄젠트함수, 소프트플러스 함수 등 좀 더 많은 활성화 함수를 만들기 위한 노력이 이어지고 있습니다.

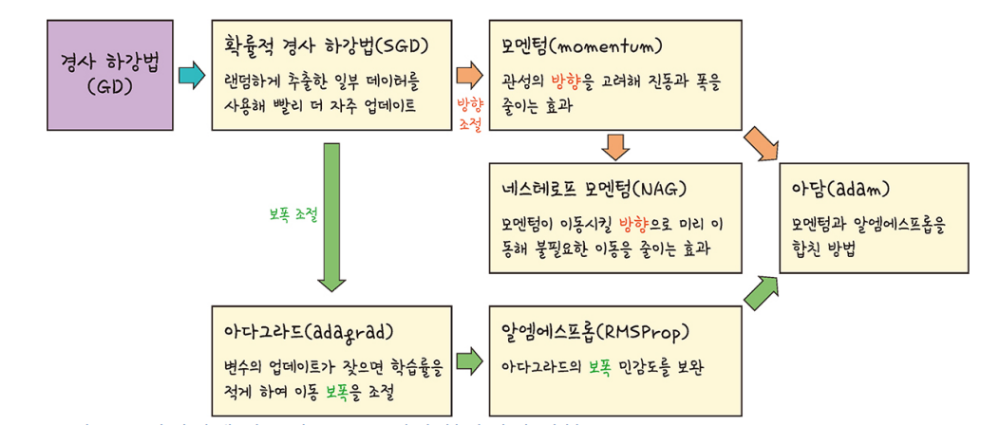
3.속도와 정확도 문제를 해결하는 고급 경사 하강법

확률적 경사 하강법
전체 데이터를 사용하는 것이 아니라, 랜덤하게 추출한 일부 데이터만 사용하여 빠르고 더 자주 업데이트가 가능함.

진폭이 크고 불안정해보이는 단점이 있지만 속도가 확연히 빠르고 최적해에 근사한 값을 찾아낸다는 장점 덕분에 경사 하강법의 대안으로 사용되고 있음.

모멘텀
경사 하강법에 탄력을 더해주는 방법 경사 하강법처럼 기울기를 구하지만, 이를 통해 오차를 수정하기 전 바로 앞 수정 값과 방향(+,-)를 참고해 같은 방향으로 일정한 비율만 수정되게 만드는 방법입니다.

지금은 정확도와 속도를 모두 향상시킨 아담(ADAM)이라는 고급 경사 하강법이 가장 많이 쓰이고 있습니다.

[출처]: 모두의 딥러닝 개정 3판 (지은이: 조태호)