[2020. 10. 24 TIL] Big-O Notation

Objectives

• Motivate the need for something like Big O Notation
• Describe what Big O Notation is
• Simplify Big O Expressions
• Define "time complexity" and "space complexity"
• Evaluate the time complexity and space complexity of different algorithms using Big O Notation
• Describe what a logarithm is

What's the idea here?

Imagine we have multiple implementations of the same function.

How can we determine which one is the "best"?

That's really what Big O is about.

< Big O >
It's a system it's a way of generalizing code and talking about it and comparing code and its performance to other pieces of code.

Who Cares?

• It's important to have a precise vocabulary to talk about how our code performs
• Useful for discussing trade-offs between different approaches.
• When your code slows down or crashes, identifying parts of the code that are inefficient can help us find pain points in our applications
• Less important : it comes up in interview! 😂

What does better code mean?

• Faster ( what we're gonna focus on )
• Less memory-intensive
• More readable

The Problem with Time

• Different machines will record different times
• The same machine will record different times
• For fast algorithms, speed measurements may not be precise enough?

If not time, then what?

• Rather than counting seconds, which are so variable...
• Let's count the number of simple operations the computer has to perform.

Counting is hard!

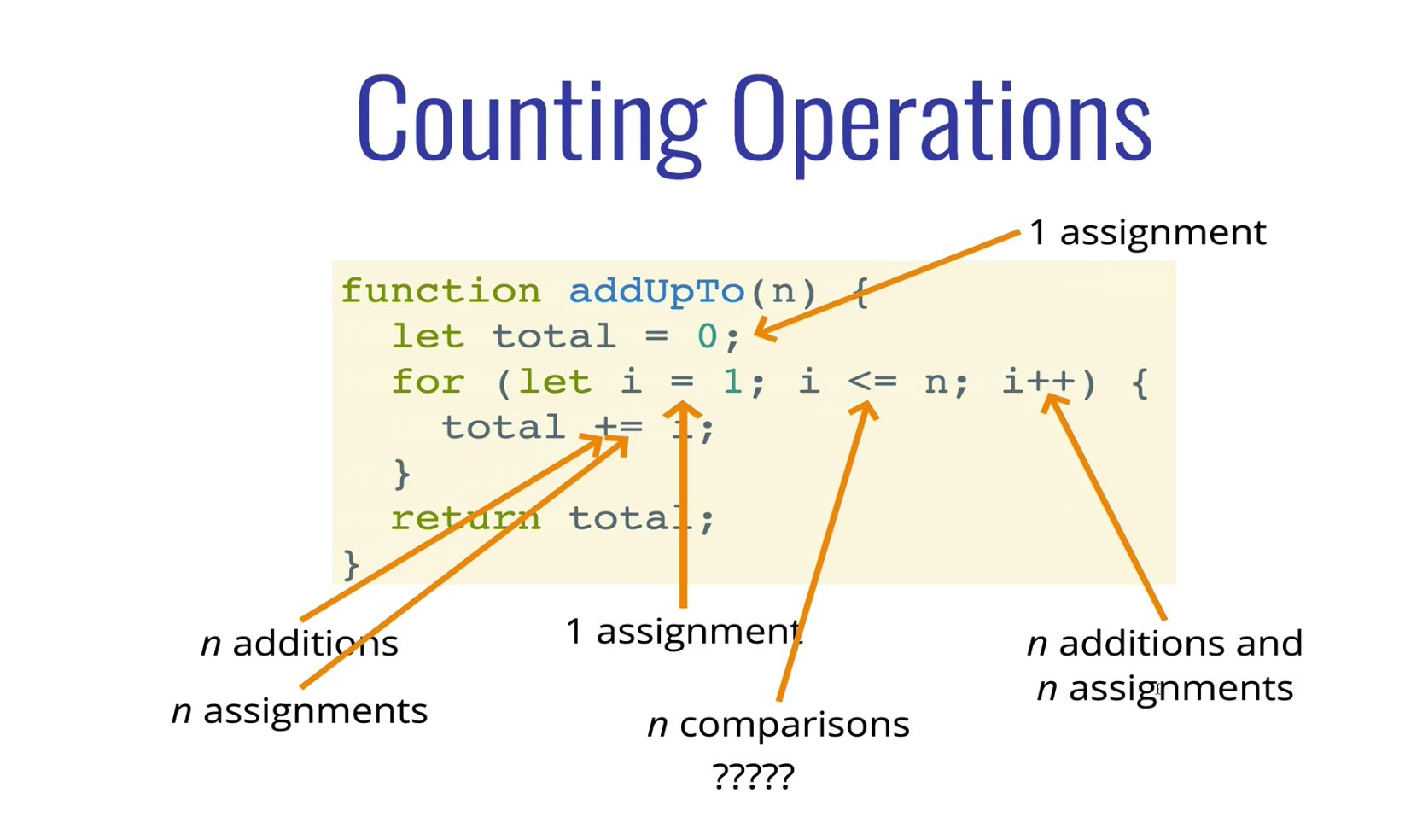
• Depending on what we count, the number of operations can be as low as 2n or as high as 5n+2
• But regardless of the exact number, the number of operations grows roughly proportionally with n
• If n doubles, the number of operations will also roughly double.

Introducing ... Big O

Big O Notation is a way to formalize fuzzy counting

It allows us to talk formally about how the runtime of an algorithm grows as the inputs grow

The relationship between the input size and then the time relative to that input.

We won't care about the details, only the trends.

We say that an algorithm is **O(f(n))** if the number of simple operations the computer has to do is eventually less than a constant times **f(n)**, as **n** increases.

f(n) could be linear (f(n) = n)
f(n) could be quadratic (f(n) = n^2)
f(n) could be constant (f(n) = 1)
f(n) could be something entirely different!

Examples

Simplify Big O expressions

When determining the time complexity of an algorithm, there are some helpful rule of thumbs for big O expressions.

These rules of thumb are consequences of the definition of big O notation.

• Constants Don't Matter
  • O(2n) → O(n)
  • O(500) → O(1)
  • O(13n²) → O(n²)
• Smaller Terms Don't Matter
  • O(n+10) → O(n)
  • O(1000n + 50) → O(n)
  • O(n² + 5n + 8) → O(n²)

Big O Shorthands

• Analyzing complexity with big O can get complicated
• There are several rules of thumb that can help
• These rules won't Always work, but are a helpful starting point
  1. Arithmetic operations are constant
  2. Variable assignment is constant
  3. Accessing elements in an array (by index) or object (by key) is constant.
  4. In a loop, the complexity is the length of the loop times the complexity of whatever happens inside of the loop

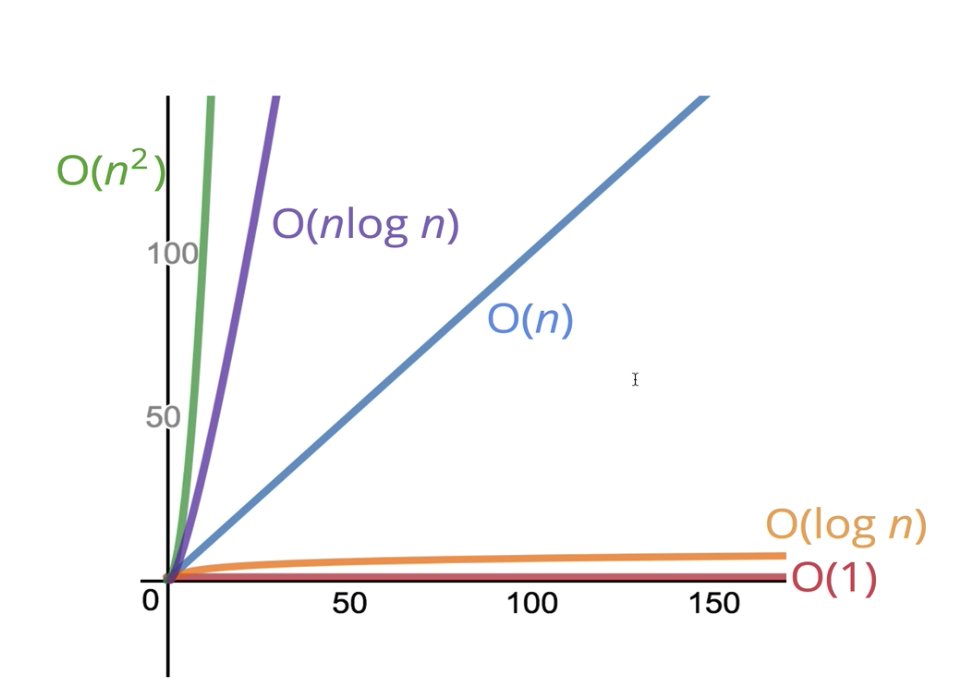
Big O Time Complexity

Space Complexity

So far, we've been focusing on time complexity

→ how can we analyze the runtime of an algorithm as the size of the inputs increase?

We can also use bit O notation to analyze space complexity

→ how much additional memory do we need to allocate in order to run the code in our algorithm?

What about the inputs?

Sometimes you'll hear the term auxiliary space complexity to refer to space required by the algorithm, not including space taken up by the inputs.

Unless otherwise noted, when we talk about space complexity, technically we'll be talking about auxiliary space complexity.

Space Complexity in JS

Rules of thumb

• Most primitives (booleans, numbers, undefined, null) are constant space.
• Strings require O(n) space (where n is the string length)
• Reference types are generally O(n), where n is the length (for arrays) or the number of keys (for objects)

Recap

• To analyze the performance of an algorithm, we use Big O Notation
• Big O Notation can give us a high level understanding of the time or space complexity of an algorithm
• Bit O Notation doesn't care about precision, only about general trends (linear? quadratic? constant?)
• The time or space complexity (as measured by Big O) depends only on the algorithm, not the hardware used to run the algorithm.
• Big O Notation is everywhere, so get lots of practice!