[KT 에이블스쿨] 4차 미니프로젝트_01

👨‍👩‍👧‍👦 4차 미니 프로젝트

미션: 서울시 공공 데이터 기반 생활인구 예측

활용 데이터셋

Train data set - 17년도 ~ 21년도 생활인구 데이터
Test data set - 22년도 생활인구 데이터

도메인 이해

상주인구 - 통계청에서는 인구 센서스를 통해 거주인구를 조사하는데 이를 상주인구 또는 야간인구라 함
유인인구 - 인구 센서스에서는 통근/통학인구를 조사하는데, 통근/통학을 통해 해당지역에 유입되는 인구를 말함
유츌인구 - 인구 센서스에서는 통근/통학인구를 조사하는데, 통근/통학을 통해 해당지역에서 타지역으로 유출되는 인구를 말함
주간인구 - 상주인구에서 유입인구를 더하고 유출인구를 뺀 인구를 말함
등록인구 - 행정기관(주민센터)에 등록하는 주민등록인구를 말함
경제활동인구 - 만 15세 이상의 생산가능 연령 인구 중에서 구직활동이 가능한 취업자 및 실업자를 말함
생활인구 - 특정시점에 특정지역에 존재하는 모든 인구이며, 현주인구(de factoPopulation) 또는 현재인구, 서비스 인구라고도 함

❗서울 생활 인구의 정의 : 서울시가 보유한 빅데이터와 KT의 통신데이터로 측정한 특정 시점에 서울의 특정 지역에 존재하는 인구

📌 즉, 거주가 아닌 특정 시점에 서울에 있다면 생활 인구로 측정되므로 서울로 출퇴근하는 시간을 주의깊게 봐야겠다.

✔️데이터 분석

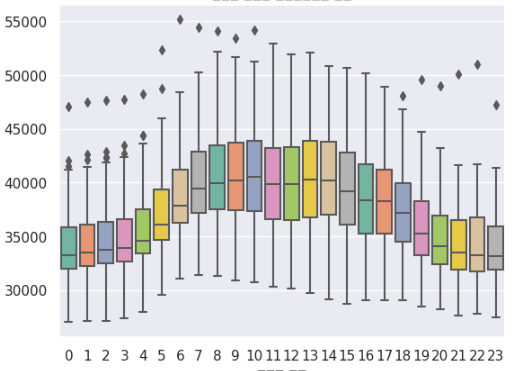
역시 예상대로 근무시간에 생활인구가 높게 측정된다. 현재 하나의 행정동을 분석한 것인데 이 지역은 근무지가 몰려있는 지역인 것이다. 따라서 근무시간에 생활인구가 높고, 새벽이나 밤에는 생활인구가 낮아지는 것을 볼 수 있다. 이것으로 더 생각해보면 20대~60대가 회사에 다니는 나이이므로 이 나이 구간도 주의 깊게 볼 필요가 있을듯하다.

이 데이터는 시계열데이터이기에 정상성을 따져볼 필요가 있다. 여기서 정상성을 띈다는 것은 시계열 데이터의 평균과 분산이 일정하다는 것이다.

from statsmodels.tsa.stattools import adfuller

def adf_test(y):
    dftest = adfuller(y, autolag='AIC')
    # autolag 'AIC' : 검정 AR 모형의 차수를 자동으로 결정
    dfoutput = pd.Series(dftest[0:4], index=['test statistic', 'p-value', '# of lags', '# of observations'])
    for key, value in dftest[4].items():
        dfoutput['Critical Value ({})'.format(key)] = value
    print(dfoutput)
adf_test(df_total['총생활인구수'])

test statistic         -8.946524e+00
p-value                 8.957713e-15
# of lags               5.500000e+01
# of observations       4.345600e+04
Critical Value (1%)    -3.430500e+00
Critical Value (5%)    -2.861607e+00
Critical Value (10%)   -2.566805e+00
dtype: float64

이어서 정규성을 띄는지 확인해보고자 했다. 여기서 정규성이란 데이터의 분포가 정규분포를 이룬다는 것이다.

from scipy import stats
from scipy.stats import shapiro
shapiro_test = stats.shapiro(df_total['총생활인구수'])
shapiro_test

from scipy.stats import anderson
anderson(df_total['총생활인구수'])

✔️데이터 전처리

깔끔한 데이터라서 이상치, 결측치등을 처리할 것이 거의 없다. 따라서 기존 데이터에서 필요한 데이터를 추출해보고자 날짜에서 연,월,일 열을 만들어서 사용할 것이다. 그리고 필요한 데이터들만 뽑아서 hour, 총생활인구수, 연, 월, 일, 이동평균 열만 사용하기로 결정했다.

# 데이터의 형식 변환
train_set['기준일ID'] = train_set['기준일ID'].apply(lambda x: x.replace('-', '')[0:8])

# '기준일ID' 열을 datetime 형식으로 변경
train_set['기준일ID'] = pd.to_datetime(train_set['기준일ID'], format='%Y%m%d')

# '연' 정보를 새로운 열로 추가
train_set['연'] = train_set['기준일ID'].dt.year

# '월' 정보를 새로운 열로 추가
train_set['월'] = train_set['기준일ID'].dt.month

# '일' 정보를 새로운 열로 추가
train_set['일'] = train_set['기준일ID'].dt.day

# 결과를 확인
print(train_set[['기준일ID', '연', '월', '일']])

훈련, 테스트 데이터 나누기
훈련 데이터셋 : 17년도 ~ 21년도
테스트 데이터 셋 : 22년도(01월~06월)

# 아래에 실습코드를 작성하고 결과를 확인합니다.

# 훈련 데이터 (train_set) 나누기
train_x = train_set.drop(['target'], axis=1)  # 'target' 열을 제외한 나머지 열을 훈련 데이터로 사용
train_y = train_set['target']  # 'target' 열을 훈련 데이터의 목표값으로 사용

# 테스트 데이터 (test_set) 나누기
test_x = test_set.drop(['target'], axis=1)  # 'target' 열을 제외한 나머지 열을 테스트 데이터로 사용
test_y = test_set['target']  # 'target' 열을 테스트 데이터의 목표값으로 사용

# 인덱스 리셋
train_x.reset_index(drop=True, inplace=True)
train_y.reset_index(drop=True, inplace=True)
test_x.reset_index(drop=True, inplace=True)
test_y.reset_index(drop=True, inplace=True)

✔️모델링

< linear >
RMSE: 842.52
R-squared Score: 0.94

from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error,r2_score
import numpy as np

model=LinearRegression()

model.fit(train_x, train_y)

# 모델을 사용하여 테스트 데이터에 대한 예측 수행
predictions = model.predict(test_x)

# RMSE 계산
rmse = np.sqrt(mean_squared_error(test_y, predictions))

# R-squared Score 계산
r2 = r2_score(test_y, predictions)

# 결과 출력
print("RMSE: {:.2f}".format(rmse))
print("R-squared Score: {:.2f}".format(r2))

< RandomForestRegressor>
RMSE: 704.57
R-squared Score: 0.96

from sklearn.ensemble import RandomForestRegressor
from sklearn.metrics import mean_squared_error,r2_score
import numpy as np

rf_model=RandomForestRegressor(n_estimators=100, random_state=42)

rf_model.fit(train_x, train_y)

# 모델을 사용하여 테스트 데이터에 대한 예측 수행
predictions = rf_model.predict(test_x)

# RMSE 계산
rmse = np.sqrt(mean_squared_error(test_y, predictions))

# R-squared Score 계산
r2 = r2_score(test_y, predictions)

# 결과 출력
print("RMSE: {:.2f}".format(rmse))
print("R-squared Score: {:.2f}".format(r2))

< GradientBoostingRegressor >
RMSE: 644.4736257455878
R-squared Score: 0.9670418438482387

from sklearn.ensemble import GradientBoostingRegressor
from sklearn.metrics import mean_absolute_error,r2_score

gb_model = GradientBoostingRegressor()

gb_model.fit(train_x,train_y)

gb_predictions = gb_model.predict(test_x)

# 평가 - RMSE
gb_rmse = mean_squared_error(test_y, gb_predictions, squared=False)
print("RMSE:", gb_rmse)

# 평가 - R-squared Score
gb_r2 = r2_score(test_y, gb_predictions)
print("R-squared Score:", gb_r2)

< Deeplearning >

import numpy as np
import tensorflow as tf

np.random.seed(0)
tf.random.set_seed(0)

X = tf.keras.Input(shape=[6])

H = tf.keras.layers.Dense(64)(X)
H = tf.keras.layers.BatchNormalization()(H)
H = tf.keras.layers.Activation('swish')(H)

H = tf.keras.layers.Dropout(0.6)(H)
H = tf.keras.layers.Dense(64)(H)
H = tf.keras.layers.BatchNormalization()(H)
H = tf.keras.layers.Activation('swish')(H)

H = tf.keras.layers.Dropout(0.5)(H)
H = tf.keras.layers.Dense(16)(H)
H = tf.keras.layers.BatchNormalization()(H)
H = tf.keras.layers.Activation('swish')(H)

H = tf.keras.layers.Dropout(0.5)(H)
H = tf.keras.layers.Dense(8)(H)
H = tf.keras.layers.BatchNormalization()(H)
H = tf.keras.layers.Activation('swish')(H)

H = tf.keras.layers.Dropout(0.3)(H)
Y = tf.keras.layers.Dense(1)(H)

model1 = tf.keras.Model(X, Y)
model1.compile(loss='mse')
# model1.summary()

model1.fit(train_x, train_y, epochs=30, batch_size=128,
          validation_split=0.2, verbose=0)
model1.fit(train_x, train_y, epochs=10,  batch_size=128, validation_split=0.2)

🚩4차 미니 프로젝트를 마치며
생활인구 예측 미니 프로젝트가 끝났다. 기본적으로 데이터가 깔끔했고, 전처리할 것이 많지않았다. 의도적으로 데이터를 만들어낼 수 있었지만 최소화해서 깔끔한 데이터로 모델링을 해보고싶었다. 결과적으로 GradientBoostingRegressor가 r2_score 0.967로 가장 좋은 결과를 나타내었다. 딥러닝 모델은 성능이 좋지 않았다. 이 전 프로젝트에서도 딥러닝 모델이 큰 성과를 내지못했는데 내가 모델링을 잘했더라면 높았을까라는 의문이 있지만 이런 결과가 계속 되니 딥러닝 모델에 대한 의문이 늘어갔다. 성능을 높일 수 있는 다향한 방법을 더 공부해봐야겠다!