Big-O 표기법
Big-O 표기법이란?
- 빅-오 라고 읽으며 점근적 상한에 대한 표기법이다.
- O(g(n))은 g(n)의 증가율보다 작거나 같은 함수들의 집합이다.
- 예를 들어 O(n2)에는 O(1), O(n), O(n log n) 등이 포함된다.
Big-O 외에도 Big-Omega(Ω) (빅-오메가) 라던지, Big-Θ (빅-세타)와 같은 다른 표기법도 존재한다. Big-Omega 표기는 최악 조건 성능 하한을 의미하고 Big-Theta 표기는 점근적인 최악 조건 성능에 있어서 그보다 나은 알고리즘은 존재하지 않는다는 의미로 사용한다. 하지만 Big-O 표기는 자주 나타나는 개념을 간략히 서술하고 대체로 별 상관이 없는 세부 정보를 생략한다는 점에서 근사를 다룰 때 큰 도움이 된다. 우리는 알고리즘을 통해 N과 어떤 관계라 있는지를 파악하여 다루는 것이 중요하지, 도출하기 어려운 표기법을 통해 정확하고 세밀한 값이 필요한게 아니다. 따라서 Big-O 표기를 통해 알고리즘의 효율성을 분석하는데 이는 Big-O 표기를 통해 불필요한 연산을 제거하여 단순화한 근사 값을 통해 알고리즘 분석을 쉽게 할 수 있기 때문이다. 이를 위해 Big-O 표기에서는 최고차항의 계수만 표기한다.
O(3n) > O(n)
O(n^2+2n) > O(n^2)
2n^3 - 9n^2 + n + 5 일 경우, 시간 복잡도는 O(n^3)
| 식 | 상한 |
|---|---|
| f(n) = 5n + 3 | O(n) |
| f(n) = 3n^2-3 | O(n^2) |
| f(n) = 5n^3-2n^2 | O(n^3) |
| O(n^2+n) | O(n^2) |
| O(n + log n) | O(n) |
| O(2^n + 100 * n^10) | O(2^n) |
| O(n + m) | O(n + m) |
Big-O 표기법의 성능
O(1) < O(log n) < O(n) < O(n * log n) < O(n²) < O(n³) < O(2^n) < O(n!)
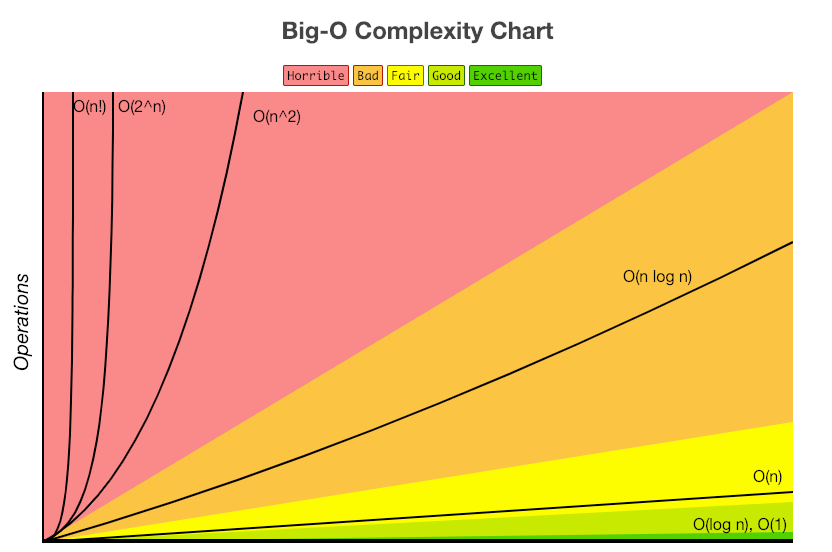
위의 그림은 알고리즘의 성능을 그래프로 나타낸 것인데 그림과 같이 O(1)부터 O(n!)으로 갈수록 성능이 좋지 않다는 것을 확인할 수 있다.
시간복잡도와 공간복잡도
Big-O 표기를 통해 알고리즘의 효율성을 나타낼 때 시간복잡도(Time Complexity)와 공간복잡도(Space Complexity)를 이용하는데 시간복잡도는 알고리즘의 연산속도를 나타내는 것이고 공간복잡도는 연산에 의한 메모리 사용량을 나타낸다.
시간복잡도
시간복잡도에서는 성능에 제일 영향을 미치는 n의 단위가 중요하다.
| 시간복잡도 | 1 | 2 | 100 |
|---|---|---|---|
| O(1) | 1 | 1 | 1 |
| O(log n) | 0 | 0.3 | 5 |
| O(n) | 1 | 2 | 100 |
| O(n * log n) | 0 | 0.6 | 461 |
| O(n^2) | 1 | 4 | 100^2 |
| O(n^3) | 1 | 8 | 100^3 |
| O(n^k),(상수 k) | 1 | 2^k | 100^k |
| O(k^n),(상수 k >1) | k | k^2 | k^100 |
| O(n!) | 1 | 2^2 | 100^100 |
n의 차수가 높고 연산 반복 값이 커질수록 값이 기하급수적으로 커진다는 것을 알 수 있다.
이는 실제로 코딩 테스트 문제에서 시간복잡도에 대한 이해력을 판단하기 위해 비교적 간단한 문제이지만 시간제한과 메모리 제한을 두는 문제가 출제 되기도 한다. 이때 이 개념을 잘 기억하고 설계해야 출제자의 의도대로 풀어낼 수 있다.
만약 데이터 개수 n이 1,000만개를 넘어가고 시간 제한이 1초라면 최악의 경우 O(n)의 시간 복잡도로 동작하는 알고리즘을 작성해야 한다.
또한 보통 연산횟수가 1초당 C언어 기준 10억번이기 때문에 이를 초과하면 오답 판정이 될 수 있다.
시간 제한이 1초인 문제의 경우
- n의 범위가 500 : 시간 복잡도가 O(n^3)인 알고리즘을 설계 시 1.25 * 10^8의 연산 횟수 필요
- n의 범위가 1,000 : 시간 복잡도가 O(n^2)인 알고리즘 설계 시 10^6^의 연산 횟수 필요
- n의 범위가 100,000 : 시간 복잡도가 O(n^2)인 알고리즘을 설계 시 10^10의 연산 횟수 필요 따라서 O(n*log n) 필요
- n의 범위가 10,000,000 : 시간 복잡도가 O(nlog n)인 알고리즘 설계 시 2.4 10^9의 연산 횟수 필요로 해결이 어려움, O(n)일 경우 10^8의 연산 횟수 천만번이 필요하고, O(log n)일 경우 약 26의 연산 횟수가 필요
따라서 n이 1000만 이상일 경우 O(n) 또는 O(log n)의 알고리즘 설계가 필요하다
공간복잡도
공간 복잡도는 Input 크기에 비례해서 알고리즘이 사용하는 메모리 공간을 나타낸다. 이 또한 Big-O 표기를 통해 나타낼 수 있다.
일반적으로 메모리 사용량 기준은 MB 단위로 제시되며 코딩 테스트 문제에서는 주로 배열, 리스트 등을 사용한다. 이때 int를 기준으로 하면 다음과 같다.
- int a[1000] : 4KB
- int a[1000000] : 4MB (10^6 * 4byte)
- int a[2000][2000] : 16MB (2000 2000 4 = 16 * 10^6byte)
일반적으로 코딩 테스트에서는 메모리 사용량을 128~512MB 정도로 제한하기 때문에 일반적인 경우에는 1,000만 단위를 넘지 않도록 하는 것이 중요하겠다.
수행시간 측정
int []arr = new int[100000000];
for(int i = 0; i < 100000000; i++) {
arr[i] = (int) Math.random();
}
long before = System.currentTimeMillis();
Arrays.sort(arr);
long after = System.currentTimeMillis();
long diff = (after - before);
System.out.println("수행결과 시간차이 : " + diff);
-------------------------------------------------
수행결과 시간차이 : 59마무리
알고리즘을 어떻게 설계하느냐에 따라서 그리고 연산을 수행할 대상의 크기가 어느정도인지에 따라서 효율적인 코드 설계를 통해 불필요한 메모리 사용이나 수행시간을 줄일 수 있을 것이다. 코딩 테스트에서도 종종 간단한 계산을 요구하지만 수행시간이나 메모리 제한을 통해 해당 개념들을 이해하는지 묻는 문제들이 출제되기도 한다. 그만큼 효율적인 코딩을 위해서라면 알고 있어야하는 개념으로 당장은 이해가 되지 않더라고 염두해두면 좋을 것 같다.
참고 velog - johngrib
참고 velog - gillog
참고 tistory - junghyungil
