[Python] 그래프 - 위상 정렬(Topology Sort) 알고리즘 구현하기

다음과 같은 조건을 가진 그래프라면 위상 정렬을 할 수 있다.

1. 간선이 방향성을 가진 그래프여야 한다.
2. 그래프 내부에 순환(Cycle)이 없어야 한다.

즉, 위상 정렬은 DAG(Direct Acyclic Graph)에 대해서만 실행할 수 있다. DAG란 순환하지 않는 방향 그래프를 말한다.

위상 정렬의 대표적인 예로 대학교의 선수과목 구조를 들 수 있다. 간단하게 말하면 B를 하기 위해 A라는 작업을 먼저 해야 하는 구조가 있을 때, 그 작업 순서를 구해주는 것이 위상 정렬이다. 위상 정렬은 여러 개의 답이 존재한다.

위상 정렬은 진입 차수를 이용해 구현하는 알고리즘으로, 큐와 스택을 이용해 두 가지 방법으로 구현할 수 있고 이 글에서는 큐로 구현하는 방법을 다루고 있다.

위상 정렬의 시간복잡도는 O(V + E) 이다.

위상 정렬 프로세스

1. 진입 차수가 0인 정점을 큐에 삽입한다.
2. 큐에서 원소를 꺼내 해당 원소에 연결된 간선을 제거한다.
3. 간선을 제거한 후 진입 차수가 0이 된 정점을 큐에 삽입한다.
4. 위 과정을 반복한다.

만약 모든 정점을 방문하기 전에 큐가 비게 된다면 사이클이 존재하는 것이다. 큐에서 원소를 꺼낸 순서가 위상 정렬의 결과가 된다.

정점과 진입차수를 저장한 그래프를 만들어 주고, 진입차수가 0인 정점 1을 큐에 삽입한다.

정점 1에 연결된 간선을 제거한 후, 진입차수가 0이 된 정점 2를 큐에 삽입한다.

정점 2에 연결된 간선 제거 후, 진입차수가 0이 된 정점 3을 큐에 삽입한다.

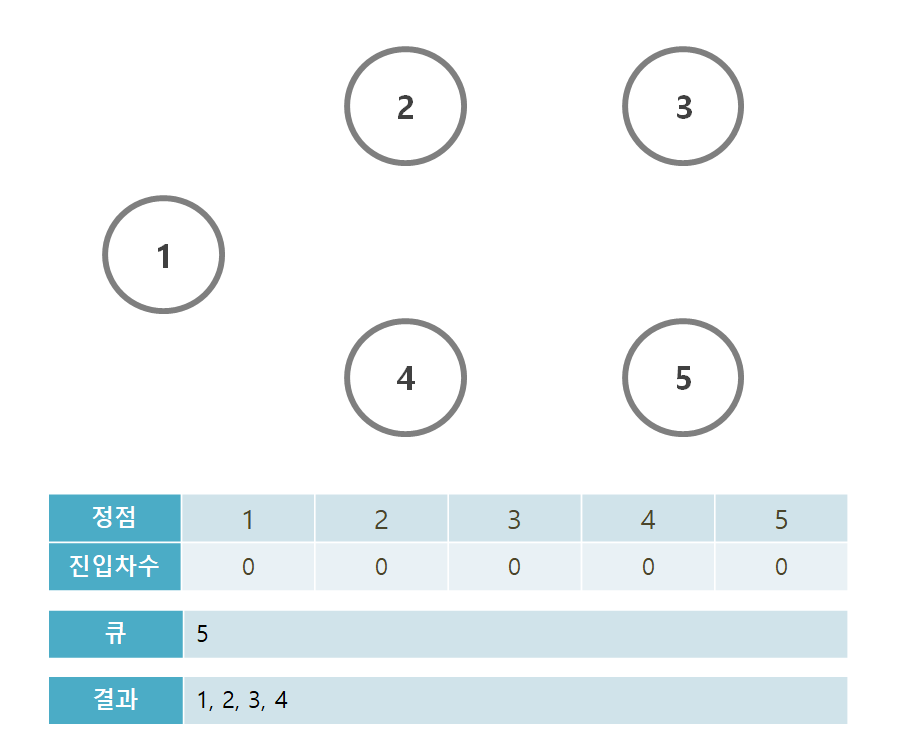
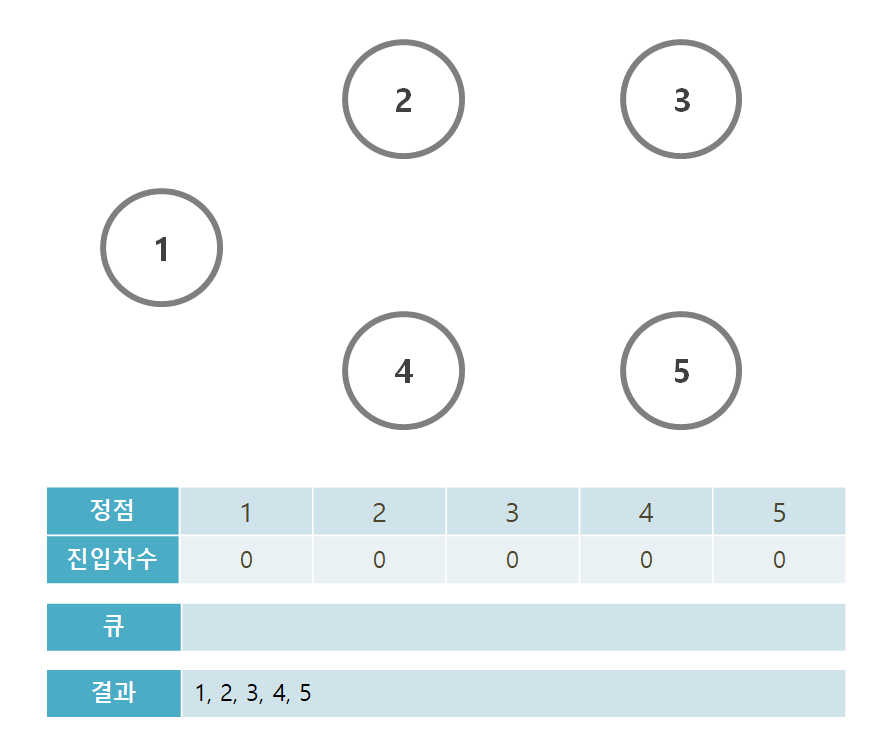
계속해서 반복해주면, 1->2->3->4->5 의 순서로 위상 정렬이 된다.

위상 정렬 구현 코드(Python)