👀 위상정렬 (Topological Sort)
위상정렬은 싸이클이 없는 방향 그래프(Directed Acyclic Graph)의 노드들을 선형적으로 정렬하는 방법이다.
이 알고리즘은 "선수과목을 고려한 학습 순서 설정"과 같이 스케줄링, 의존성 관리, 작업 순서 결정 등에 많이 사용된다.
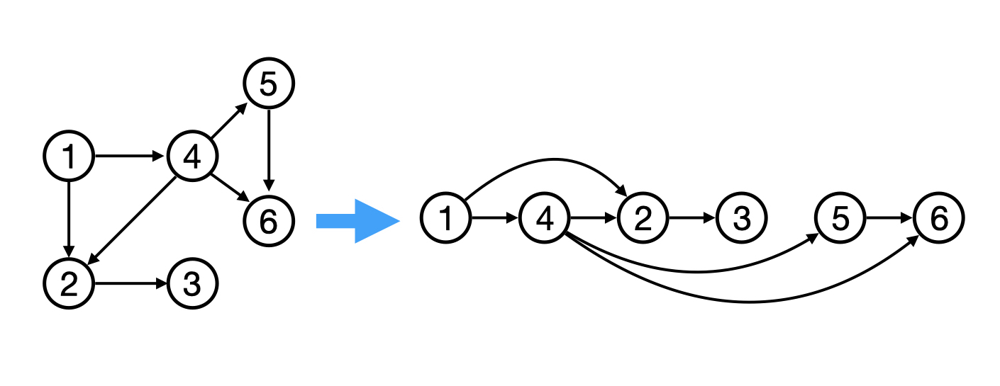
🤔 진입차수(Indegree)란?
진입차수란 특정 노드로 들어오는 간선의 개수를 의미한다.
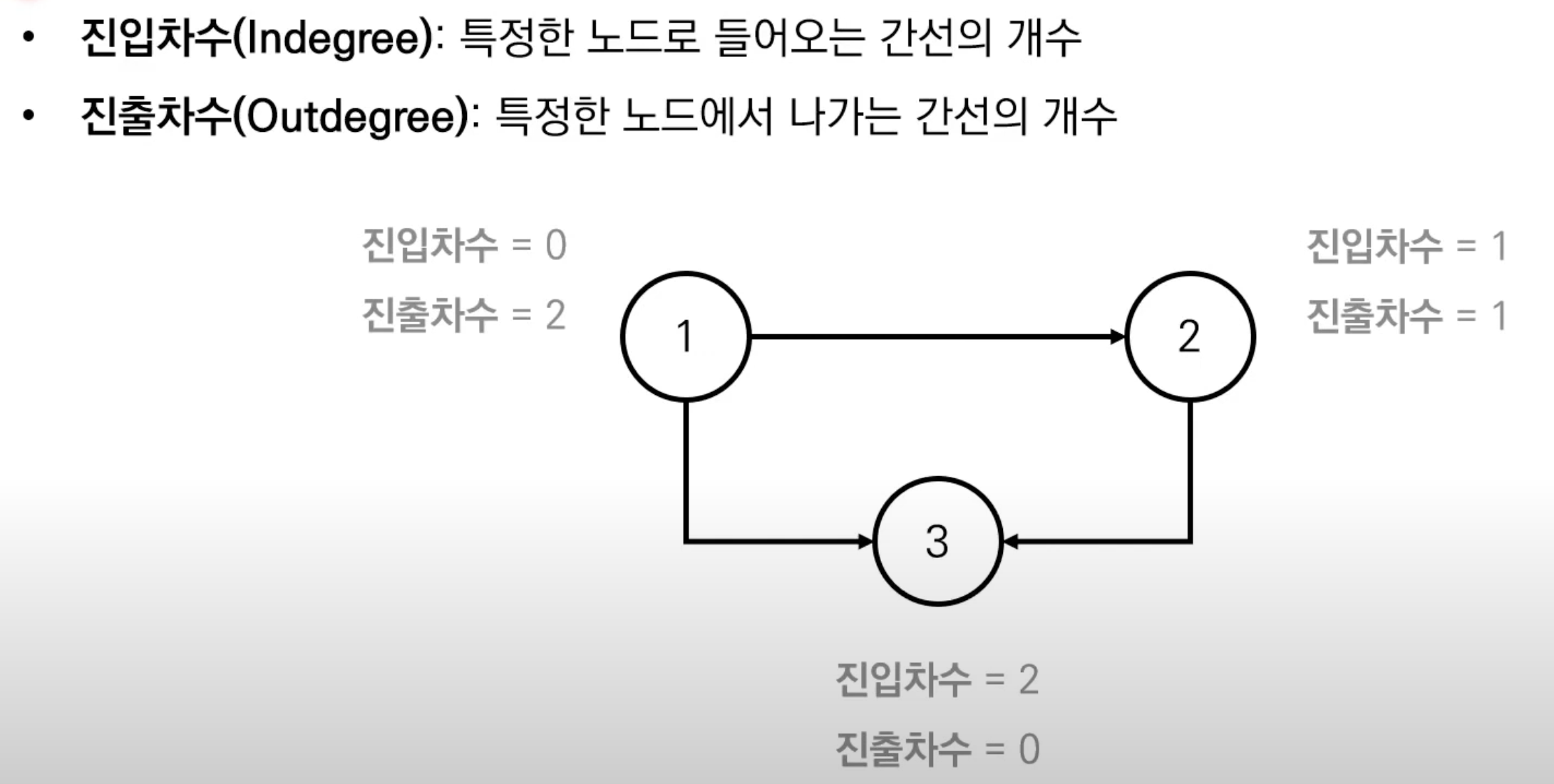
👩🏻💻 위상정렬 풀이 방법
1) 진입차수가 0인 모든 노드를 큐에 넣는다.
2) 큐가 빌 때까지 다음의 과정을 반복한다.
- 큐에서 원소를 꺼내 해당 노드에서 나가는 간선을 그래프에서 제거한다.
- 새롭게 진입 차수가 0이 된 노드를 큐에 넣는다.
👉🏻 결과적으로 큐에 노드가 들어온 순서가 위상정렬을 수행한 결과와 같다.
📝 위상정렬 Cheat Sheet
from collections import deque
# 노드의 개수와 간선의 개수를 입력 받기
v, e = map(int, input().split())
# 모든 노드에 대한 진입차수는 0으로 초기화
indegree = [0] * (v + 1)
# 각 노드에 연결된 간선 정보를 담기 위한 연결 리스트 초기화
graph = [[] for i in range(v + 1)]
# 방향 그래프의 모든 간선 정보를 입력 받기
for _ in range(e):
a, b = map(int, input().split())
graph[a].append(b) # 정점 A에서 B로 이동 가능
# 진입 차수를 1 증가
indegree[b] += 1
# 위상 정렬 함수
def topology_sort():
result = [] # 알고리즘 수행 결과를 담을 리스트
q = deque() # 큐 기능을 위한 deque 라이브러리 사용
# 처음 시작할 때는 진입차수가 0인 노드를 큐에 삽입
for i in range(1, v + 1):
if indegree[i] == 0:
q.append(i)
# 큐가 빌 때까지 반복
while q:
# 큐에서 원소 꺼내기
now = q.popleft()
result.append(now)
# 해당 원소와 연결된 노드들의 진입차수에서 1 빼기
for i in graph[now]:
indegree[i] -= 1
# 새롭게 진입차수가 0이 되는 노드를 큐에 삽입
if indegree[i] == 0:
q.append(i)
# 위상 정렬을 수행한 결과 출력
for i in result:
print(i, end=' ')
topology_sort()LeetCode 207. Course Schedule
🔗 문제

📝 답안
위상정렬을 한 결과를 result 배열에 담는데, 만약 이 result 배열에 모든 노드(= 과목)가 들어가지 못하면 모든 코스를 완료할 수 없음을 의미한다.
from collections import deque
class Solution(object):
def canFinish(self, numCourses, prerequisites):
"""
:type numCourses: int
:type prerequisites: List[List[int]]
:rtype: bool
"""
# 모든 과목에 대한 진입 차수는 0으로 초기화
indegree = [0] * numCourses
# 각 과목에 연결된 간선 정보를 담기 위한 그래프 초기화
graph = [[] for _ in range(numCourses)]
# 선수 과목 관계를 그래프에 반영하기
for edge in prerequisites:
u, v = edge # 수업 u를 듣기 위해선 v를 먼저 들어야 함
graph[v].append(u) # v -> u
indegree[u] += 1 # u의 진입 차수 1 증가
result = [] # 수강할 수 있는 과목 목록
q = deque()
# 진입 차수가 0인 과목들을 큐에 삽입
for i in range(numCourses):
if indegree[i] == 0:
q.append(i)
# 큐가 빌 때까지 반복
while q:
now = q.popleft()
result.append(now)
for i in graph[now ]:
# now 과목과 연결된 노드들의 진입 차수에서 1 빼기
indegree[i] -= 1
# 새롭게 진입 차수가 0이 되는 과목들을 큐에 삽입
if indegree[i] == 0:
q.append(i)
# 들을 수 있는 과목 수가 numCourses보다 적으면 False 리턴
return len(result) == numCourses백준 2252번 줄 세우기
🔗 문제
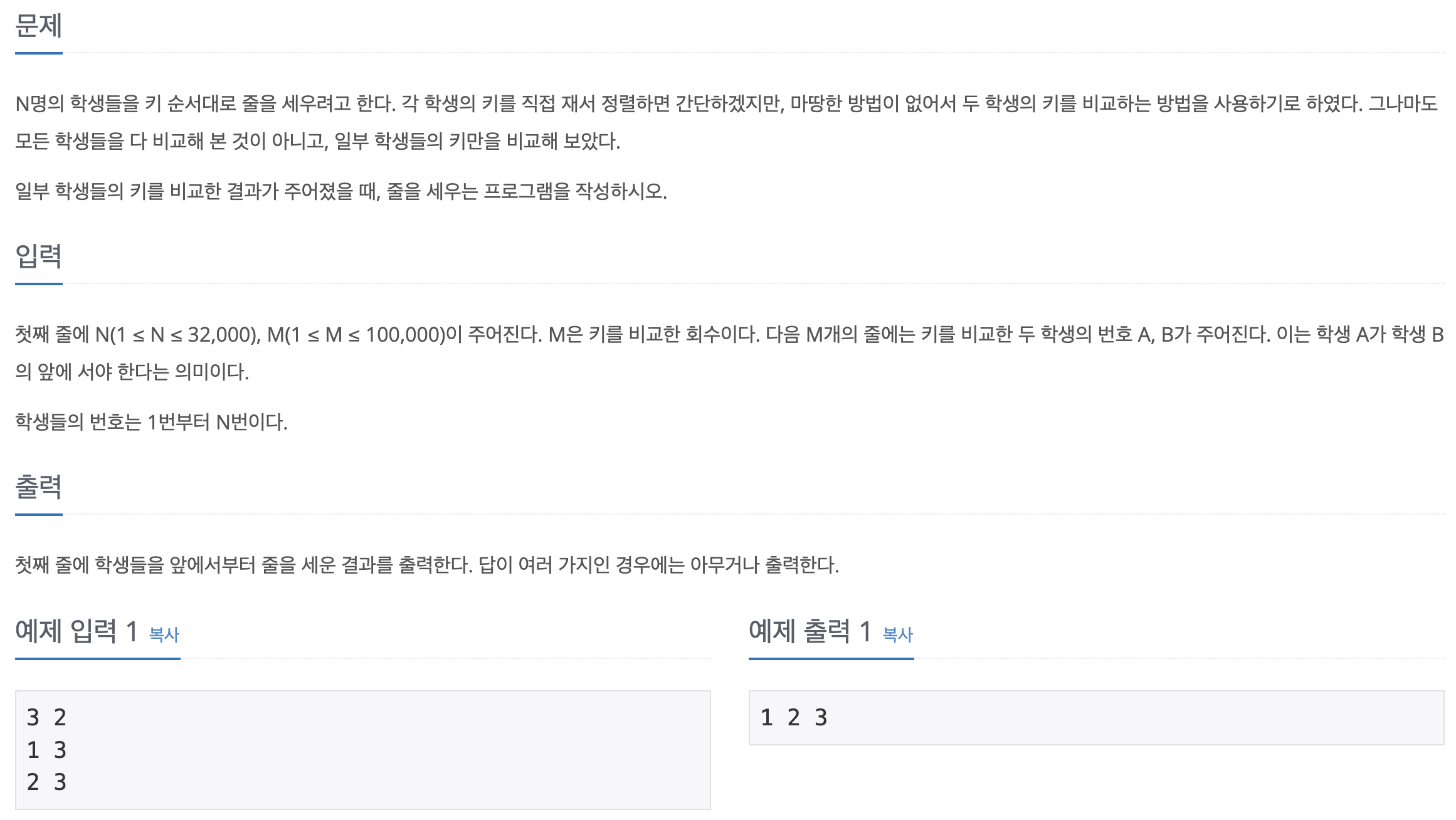
📝 답안
import sys
from collections import deque
input = sys.stdin.readline
n, m = map(int, input().split())
# 정점 연결 정보
graph = [[] for i in range(n + 1)]
# 모든 노드에 대한 진입 차수는 0으로 초기화
indegree = [0] * (n + 1)
# 비교(간선) 정보 입력 받기
for _ in range(m):
a, b = map(int, input().split())
# a 보다 큰 노드로 b 추가
graph[a].append(b)
# b의 진입차수 1 증가
indegree[b] += 1
# 위상 정렬 함수
def topology_sort():
result = [] # 키 순서대로 정렬
q = deque()
# 처음 시작할 때는 진입 차수가 0인 노드를 큐에 삽입. 즉 가장 작은 학생
for i in range(1, n + 1):
if indegree[i] == 0:
q.append(i)
# 큐가 빌 때까지 반복
while q:
now = q.popleft()
result.append(now)
# 해당 원소와 연결된 노드들의 진입 차수에서 1 빼기
for i in graph[now]:
indegree[i] -= 1
# 새롭게 진입 차수가 0이 되는 노드를 큐에 삽입
if indegree[i] == 0:
q.append(i)
for i in result:
print(i, end=" ")
topology_sort()백준 2637번 장난감 조립
🔗 문제
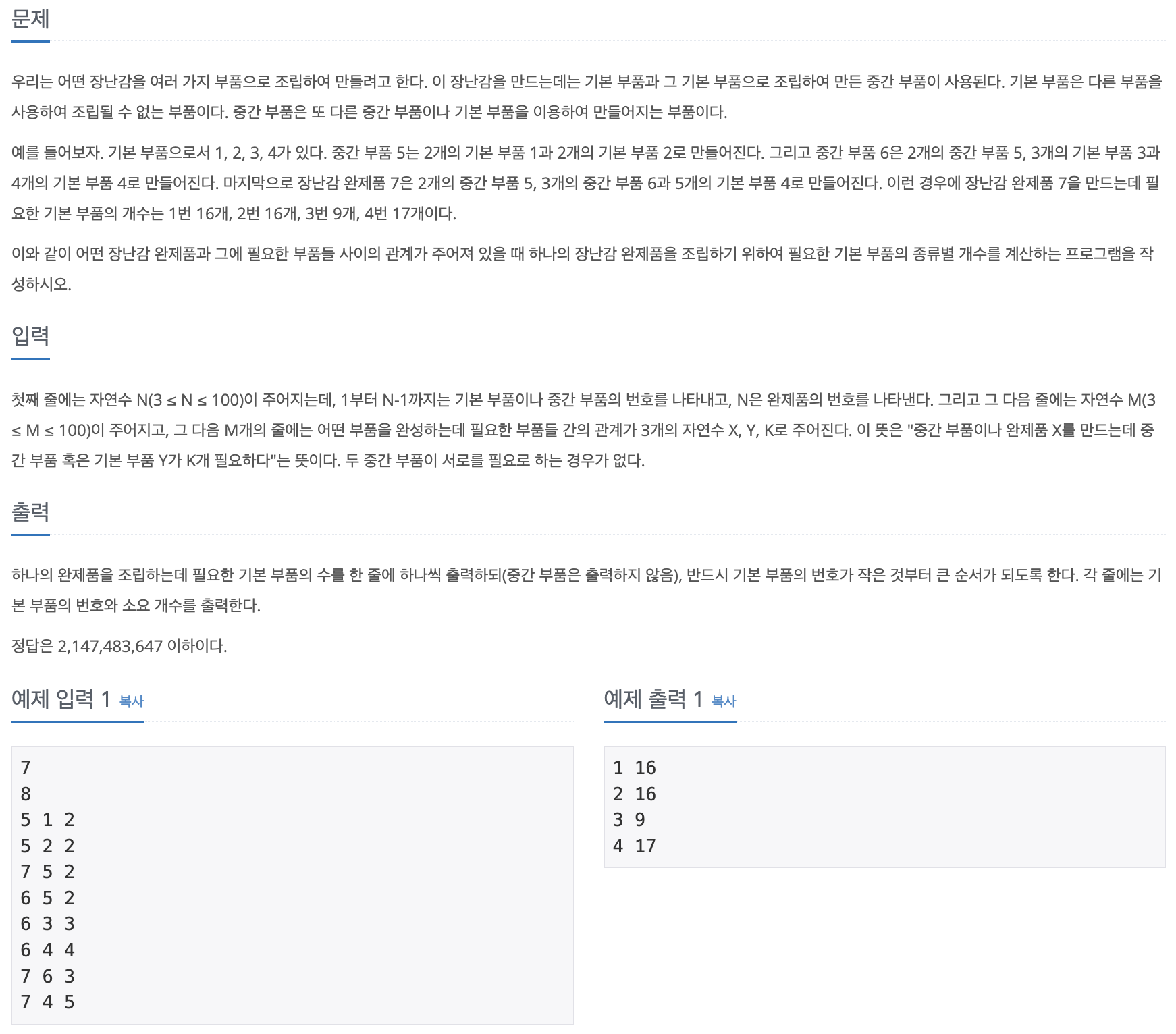
📝 답안
import sys
from collections import deque
input = sys.stdin.readline
n = int(input().strip())
connect = [[] for _ in range(n + 1)] # 연결 정보
needs = [[0] * (n + 1) for _ in range(n + 1)] # 각 제품을 만들때 필요한 부품
q = deque() # 위상 정렬
degree = [0] * (n + 1) # 진입 차수
for _ in range(int(input())):
a, b, c = map(int, input().split()) # a를 만드는데 b가 c개 필요
connect[b].append((a, c))
degree[a] += 1
for i in range(1, n + 1):
# 진입 차수가 0인걸 넣어준다.
if degree[i] == 0:
q.append(i)
# 위상 정렬 시작
while q:
now = q.popleft()
# 현 제품의 다음 단계 번호, 현 제품이 얼마나 필요한지
for next, next_need in connect[now]:
# 만약 현 제품이 기본 부품이면
if needs[now].count(0) == n + 1:
needs[next][now] += next_need
# 현 제품이 중간 부품이면
else:
for i in range(1, n + 1):
needs[next][i] += needs[now][i] * next_need
# 차수 -1
degree[next] -= 1
if degree[next] == 0:
# 차수 0이면 큐에 넣음
q.append(next)
for x in enumerate(needs[n]):
if x[1] > 0:
print(*x)백준 1432번 그래프 수정
🔗 문제
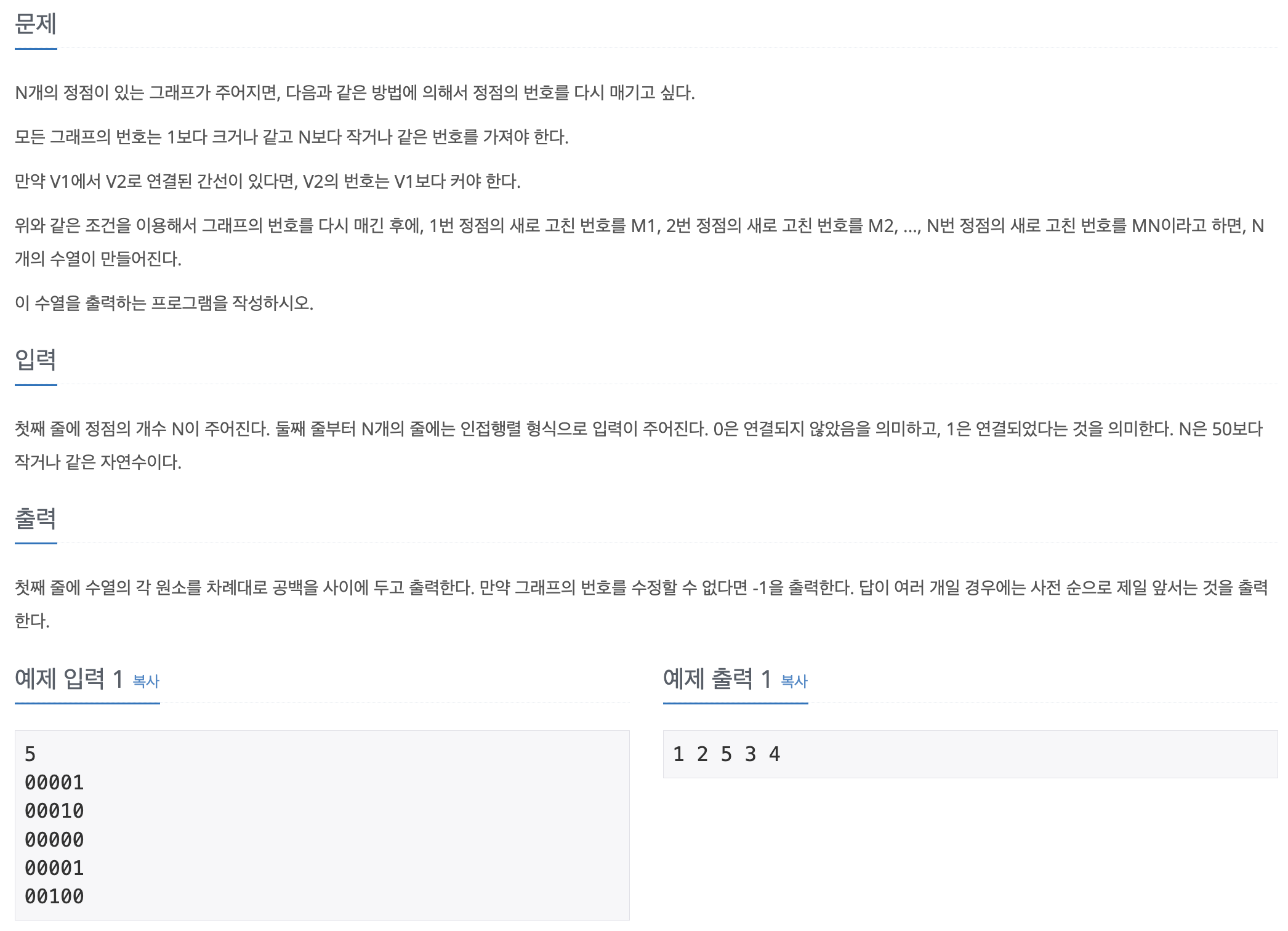
📝 답안
import sys
import heapq
input = sys.stdin.readline
n = int(input().strip())
# 각 노드에 연결된 간선 정보를 담기 위한 연결 리스트 초기화
graph = [[] for _ in range(n + 1)]
# 모든 노드에 대한 진출차수는 0으로 초기화
outdegree = [0] * (n + 1)
# 결과 저장 배열
result = [0] * (n + 1)
for i in range(1, n + 1):
connection = list(map(int, input().strip()))
for idx, val in enumerate(connection, start=1):
if val == 1:
graph[idx].append(i)
outdegree[i] += 1
# 위상 정렬
def topology_sort(n):
heap = []
for i in range(1, n + 1):
if outdegree[i] == 0:
heapq.heappush(heap, -i)
while heap:
now = -heapq.heappop(heap)
result[now] = n
for connected_node in graph[now]:
outdegree[connected_node] -= 1
if outdegree[connected_node] == 0:
heapq.heappush(heap, -connected_node)
n -= 1
topology_sort(n)
if result.count(0) > 2:
print(-1)
else:
print(' '.join(map(str, result[1:])))백준 1948번 임계경로
🔗 문제
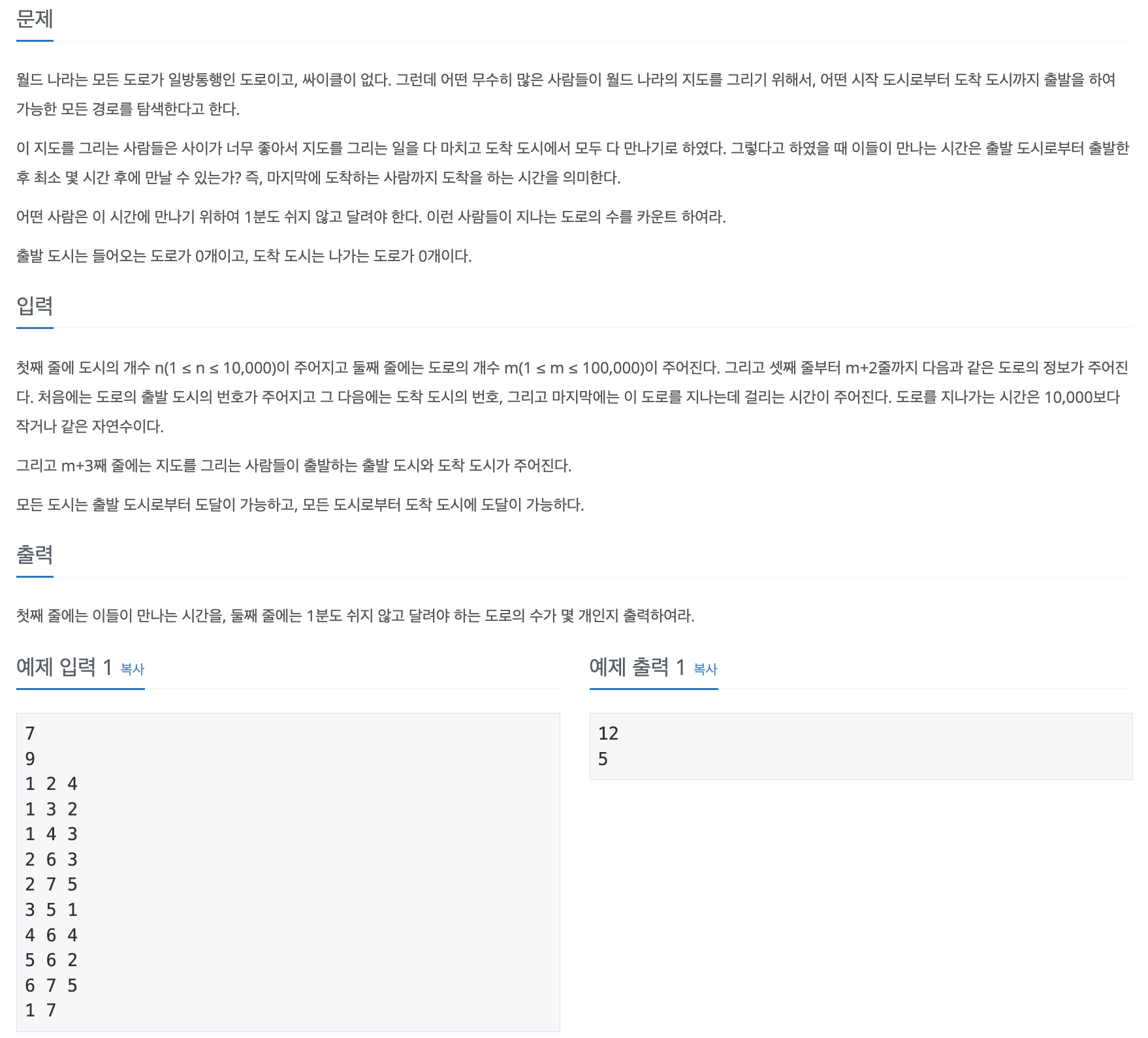
📝 답안
import sys
from collections import deque
n=int(input()) #노드, 도시 개수
m=int(input()) #도로의 개수
graph = [[] * (n + 1) for _ in range(n + 1)]
back_graph = [[] * (n +1) for _ in range(n + 1)]
indegree = [0] * (n + 1)
result = [0] * (n + 1)
check = [0] * (n + 1)
q = deque()
for _ in range(m):
a, b ,t = map(int,input().split())
graph[a].append((b,t))
back_graph[b].append((a,t))
indegree[b]+=1
start,end=map(int,input().split())
q.append(start)
def topology():
while q:
cur = q.popleft()
for i, t in graph[cur]:
indegree[i] -= 1
result[i] = max(result[i], result[cur] + t)
if indegree[i] == 0:
q.append(i)
# 백트래킹
cnt = 0 # 임계 경로에 속한 모든 정점의 개수
q.append(end)
while q:
cur = q.popleft()
for i, t in back_graph[cur]:
if result[cur] - result[i] == t:
cnt += 1
if check[i] == 0:
q.append(i)
check[i] = 1
print(result[end])
print(cnt)
topology()