🧐 다이나믹 프로그래밍이란?
다이나믹 프로그래밍이란 문제를 효율적으로 풀기 위해 복잡한 큰 문제를 더 작은 하위 문제로 나누어 푸는 방법이다.
이 방법은 동일한 하위 문제를 반복해서 풀지 않고, 중복되는 계산을 제거하여 효율적으로 문제를 풀 수 있다.
다이나믹 프로그래밍 구현 방법은 크게 top-down 방식과 bottom-up 방식으로 나누어 살펴볼 수 있다.
⬇️ top-down 방식
top-down 방식은 큰 문제를 작은 하위 문제로 나누고, 각 하위 문제의 해결을 위해 재귀 함수를 호출한다.
이 때 중복 계산을 피하기 위해 메모이제이션 기법을 사용하여 계산한 결과를 메모리 공간에 메모해놓고, 같은 문제가 다시 호출되면 메모했던 결과를 그대로 가져온다.
⬆️ bottom-up 방식
bottom-up 방식은 작은 하위 문제부터 시작해서 큰 문제까지 순차적으로 해결해나가는 방법인데, 계산한 값을 dp 테이블에 저장해나가는 방식을 사용한다.
일반적으로 재귀보다 반복문이 속도가 더 빠르므로, top-down 방식을 bottom-up 방식으로 바꾸려고 시도하는 경우가 많다.
백준 2748번 피보나치 수 2
📄 문제
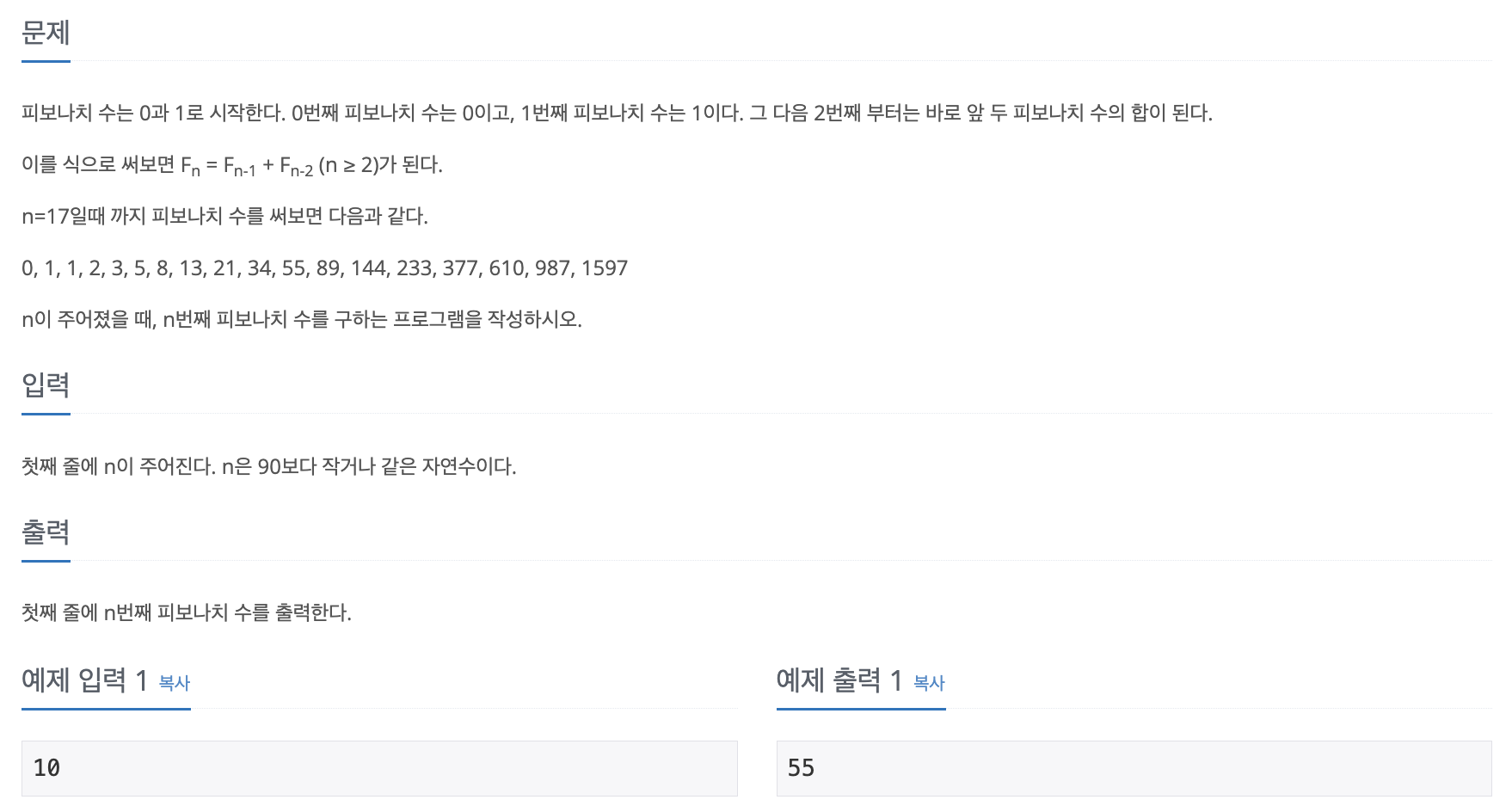
📝 답안
1) 시간복잡도: O(2^n)
import sys
n = int(sys.stdin.readline().strip())
result = [0] * (n + 1)
def fibonacci(n):
if n == 1 or n == 2:
result[n] = 1
return 1
# 메모이제이션
if result[n]:
return result[n]
result[n] = fibonacci(n - 1) + fibonacci(n - 2)
return result[n]
print(fibonacci(n))2) 시간복잡도: O(n)
import sys
n = int(sys.stdin.readline().strip())
result = [0] * (n + 1)
def fibonacci(n):
if n <= 1:
return n
fib = [0] * (n + 1)
fib[1] = 1
for i in range(2, n + 1):
fib[i] = fib[i - 1] + fib[i - 2]
return fib[n]
print(fibonacci(n))백준 2624번 동전 바꿔주기
📄 문제
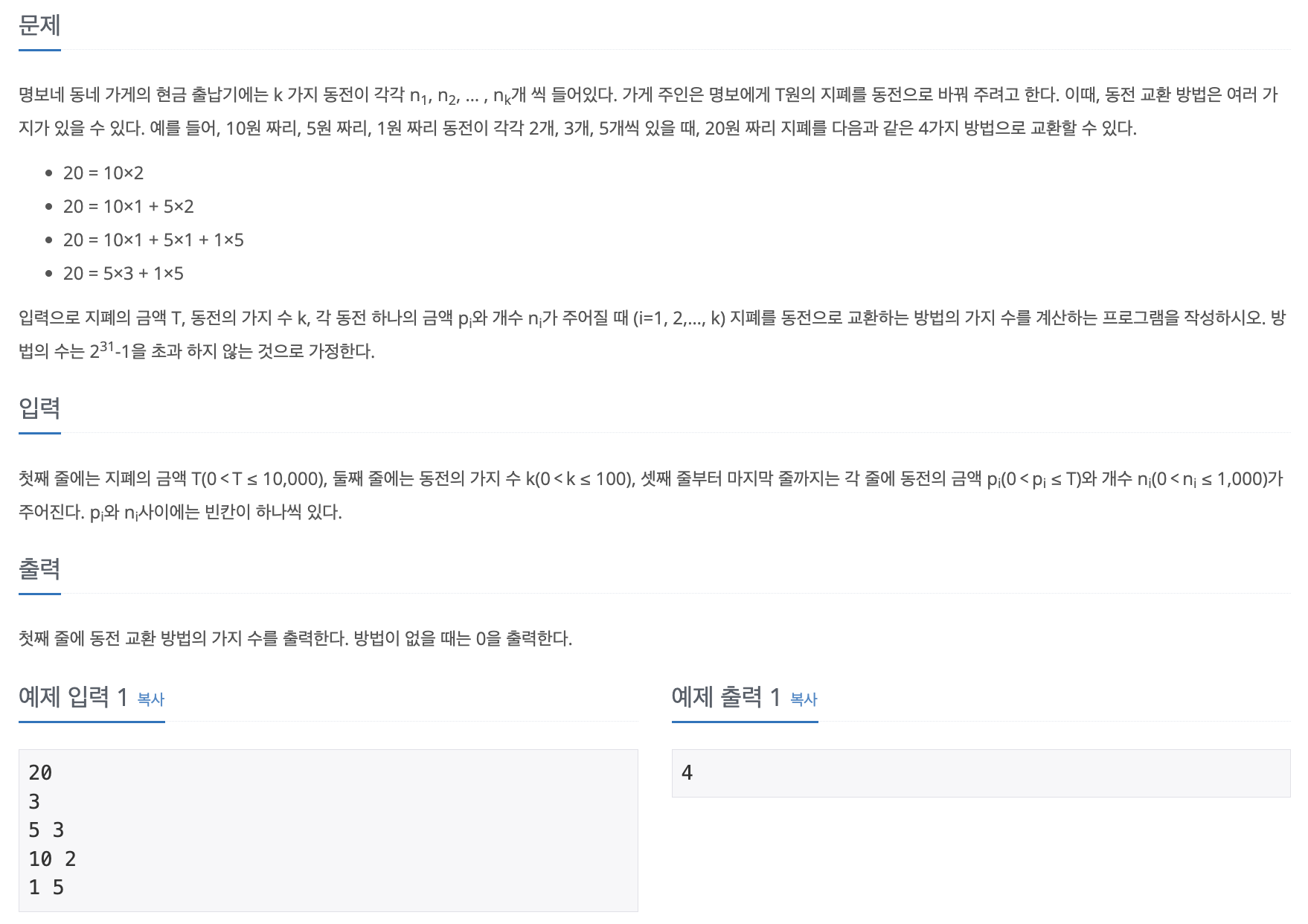
📝 답안
import sys
input = sys.stdin.readline
# 지폐의 금액
T = int(input().strip())
# 동전의 가지 수
k = int(input().strip())
# 동전 정보
coins = []
for _ in range(k):
p, n = map(int, input().split())
coins.append((p, n))
# 금액 n에 대한 동전 교환 방법의 가지 수
dp = [0] * (T + 1)
# 0원인 경우 교환 방법은 한 가지이므로 1로 초기화
dp[0] = 1
# 동적 프로그래밍
for coin, cnt in coins:
for money in range(T, 0, -1): # 목표금액에서 1원까지 내려가며 진행
for i in range(1, cnt + 1): # 현재 동전 coin의 개수 cnt만큼 반복문 진행
if money - coin * i >= 0:
# coin을 i개 사용했을 때 금액 money를 만들 수 있는 경우의 수는
# 나머지 금액 money - coin * i를 만들 수 있는 경우의 수와 같음
dp[money] += dp[money - coin * i]
print(dp[T])백준 9084번 동전
📄 문제
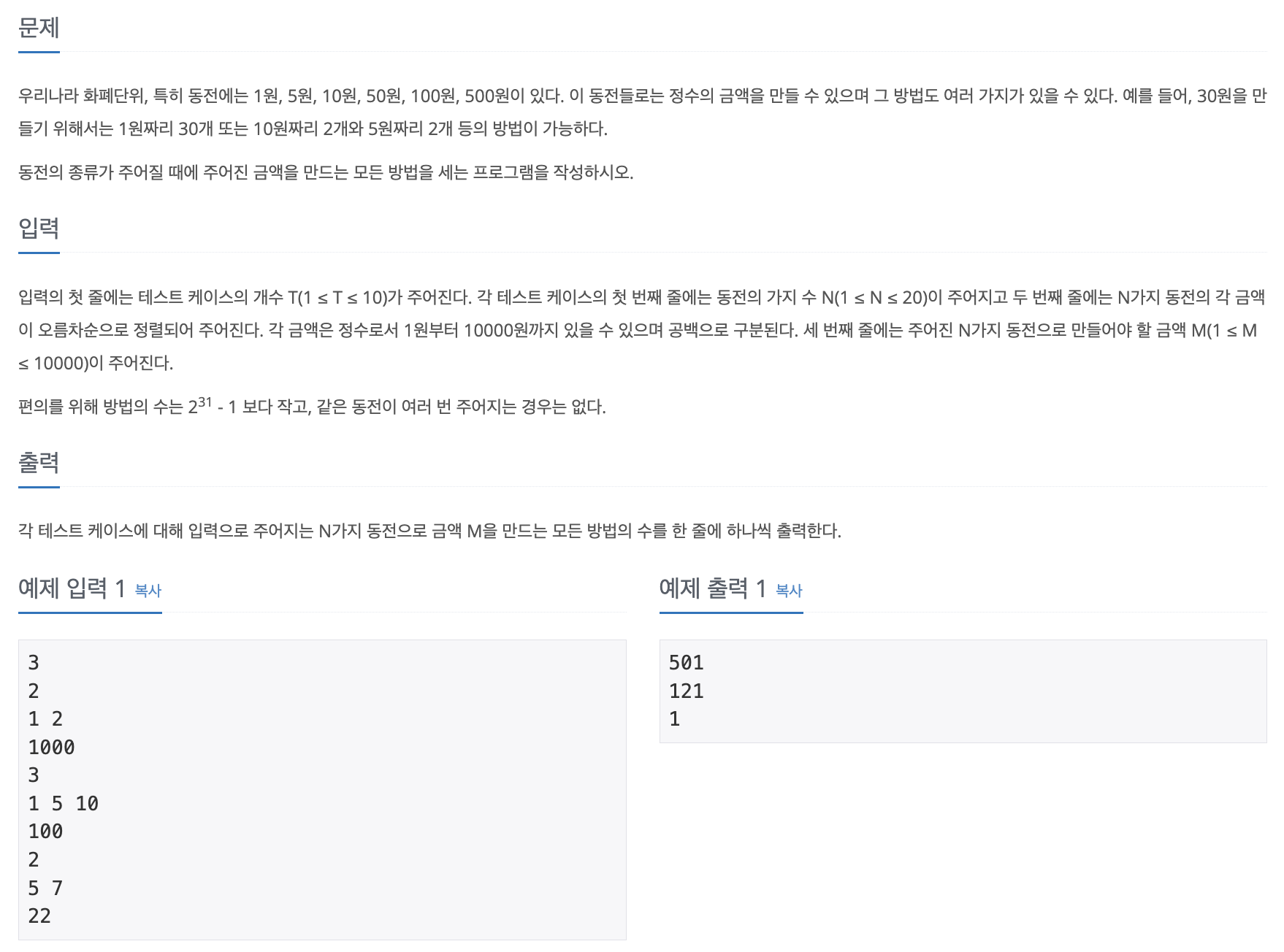
📝 답안
아래 그림과 같이 동전을 사용한 경우와 사용하지 않은 경우를 나누어서 재귀 함수를 활용해서 푼 방법이다.
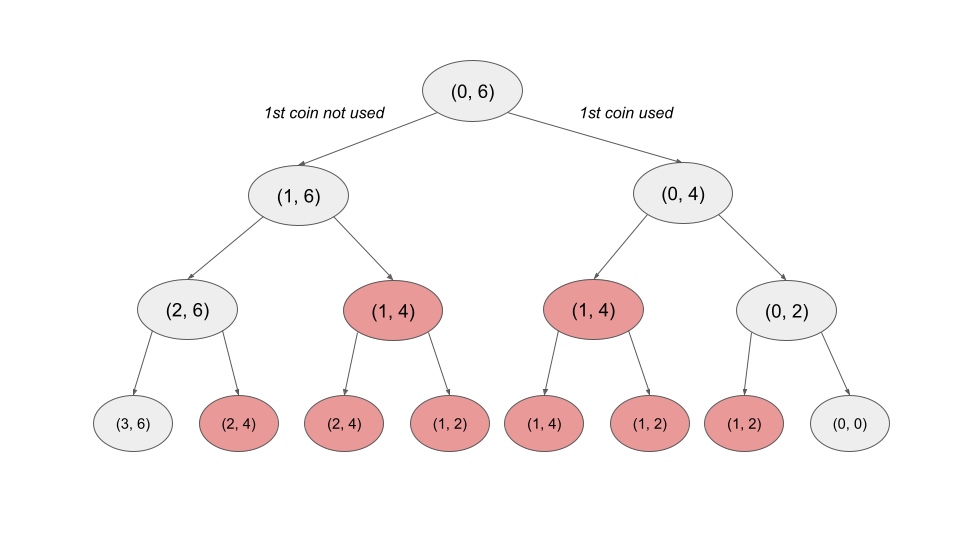
import sys
input = sys.stdin.readline
def solution(T, coins):
# 메모이제이션
memo = [[-1] * (T + 1) for _ in range(len(coins))]
# 가능한 경우의 수 세기
def number_of_ways(i, amount): # i: 현재 동전의 인덱스 / amount: 남은 금액
if amount == 0: # 목표한 금액을 만들면 1 리턴
return 1
if i == len(coins): # 목표한 금액을 만들지 못한 상태로 동전 배열의 끝에 도달하면 0 리턴
return 0
if memo[i][amount] != -1: # 이미 가능한 경우의 수를 셌다면 중복 계산 없이 해당 값 리턴
return memo[i][amount]
if coins[i] > amount: # 만약 남은 금액보다 현재 동전의 금액이 크다면 다음 동전으로 넘어가기
memo[i][amount] = number_of_ways(i + 1, amount)
return memo[i][amount]
else:
# 현재 동전을 포함했을 때와 포함하지 않았을 때의 경우의 수를 합함
memo[i][amount] = number_of_ways(i, amount - coins[i]) + number_of_ways(i + 1, amount)
return memo[i][amount]
return number_of_ways(0, amount)
case = int(input().strip())
for _ in range(case):
coin_n = int(input().strip())
coins = sorted(list(map(int, input().strip().split())), reverse=True)
amount = int(input().strip())
print(solution(amount, coins))백준 2294번 동전 2
📄 문제
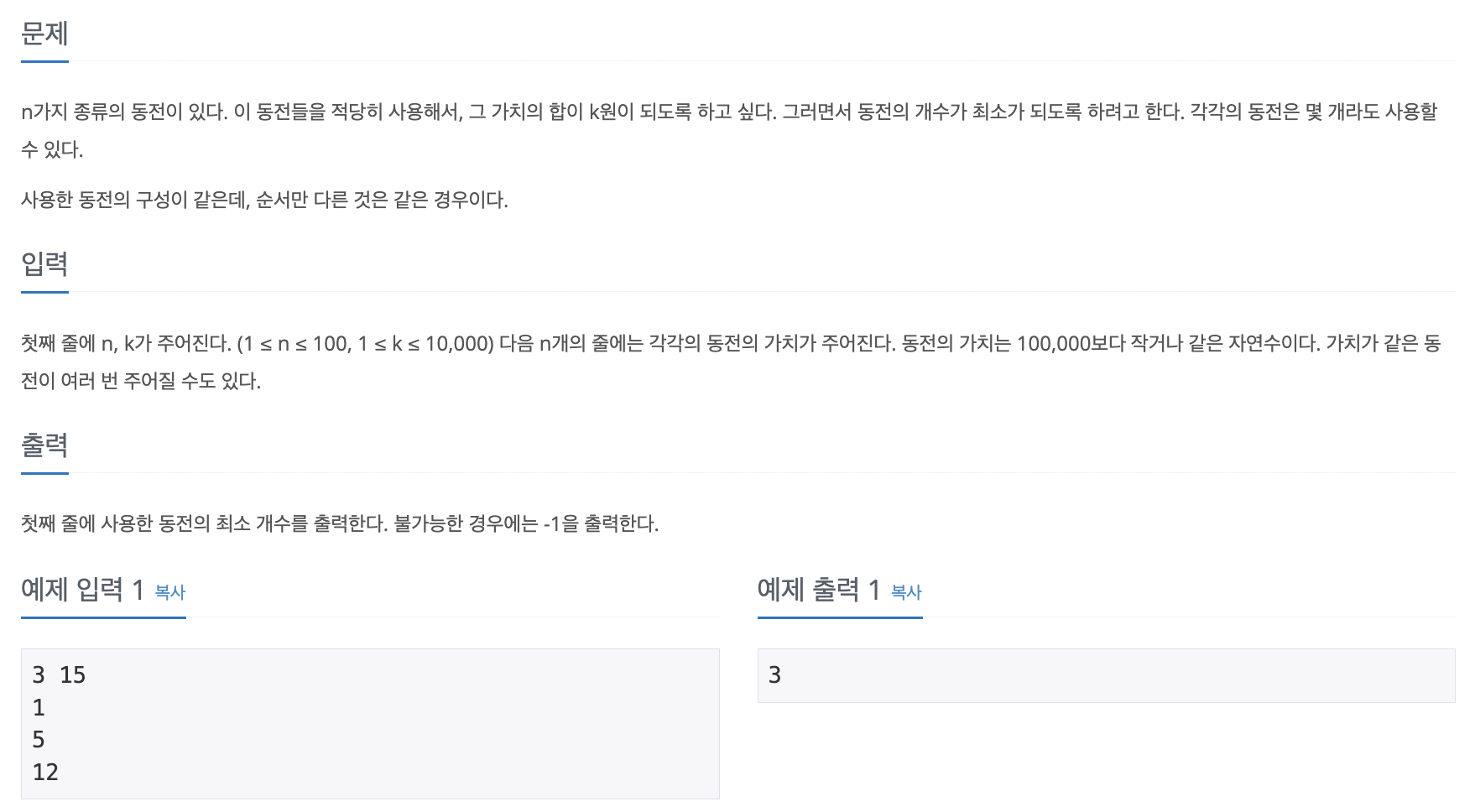
📝 답안
import sys
input = sys.stdin.readline
# n: 동전 종류의 개수, k: 만들려는 금액
n, k = map(int, input().strip().split())
# 동전 종류별 금액
coins = sorted([int(input().strip()) for _ in range(n)])
coins = set(coins)
# 동전 개수 테이블
nums = [10001] * (k + 1)
nums[0] = 0
for coin in coins:
for i in range(coin, k + 1):
nums[i] = min(nums[i], nums[i-coin] + 1)
if nums[k] == 10001:
print(-1)
else:
print(nums[k])백준 9251번 LCS
📄 문제
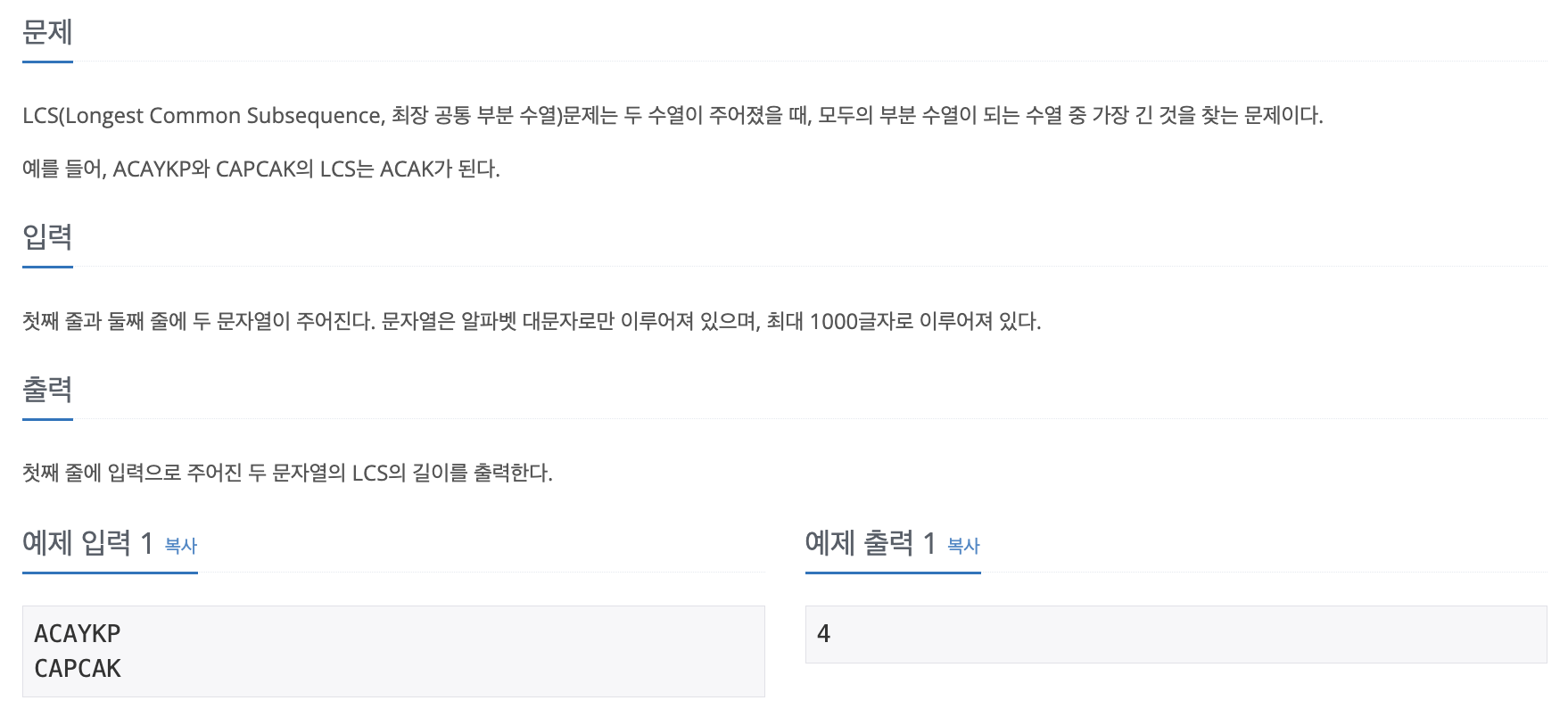
📝 답안
자세한 풀이는 이 포스팅에 작성함
import sys
first = sys.stdin.readline().strip()
second = sys.stdin.readline().strip()
def longest_common_subsequence(text1: str, text2: str) -> int:
dp_grid = [[0] * (len(text2) + 1) for _ in range(len(text1) + 1)]
for col in reversed(range(len(text2))):
for row in reversed(range(len(text1))):
if text2[col] == text1[row]:
dp_grid[row][col] = 1 + dp_grid[row + 1][col + 1]
else:
dp_grid[row][col] = max(dp_grid[row + 1][col], dp_grid[row][col + 1])
return dp_grid[0][0]
print(longest_common_subsequence(first, second))LeetCode 70. Climbing Stairs
📄 문제

📝 답안
class Solution(object):
def climbStairs(self, n):
"""
:type n: int
:rtype: int
"""
def dfs(rest, memo):
if rest == 0:
return 1
if rest < 0:
return 0
if rest in memo:
return memo[rest]
memo[rest] = dfs(rest - 1, memo) + dfs(rest - 2, memo)
return memo[rest]
memo = {}
return dfs(n, memo)300. Longest Increasing Subsequence
📄 문제

📝 답안
class Solution(object):
def lengthOfLIS(self, nums):
"""
:type nums: List[int]
:rtype: int
"""
n = len(nums)
dp = [1] * n
for i in range(1, n):
for j in range(i):
if nums[i] > nums[j]:
dp[i] = max(dp[i], dp[j] + 1)
return max(dp)백준 10942번 팰린드롬?
📄 문제
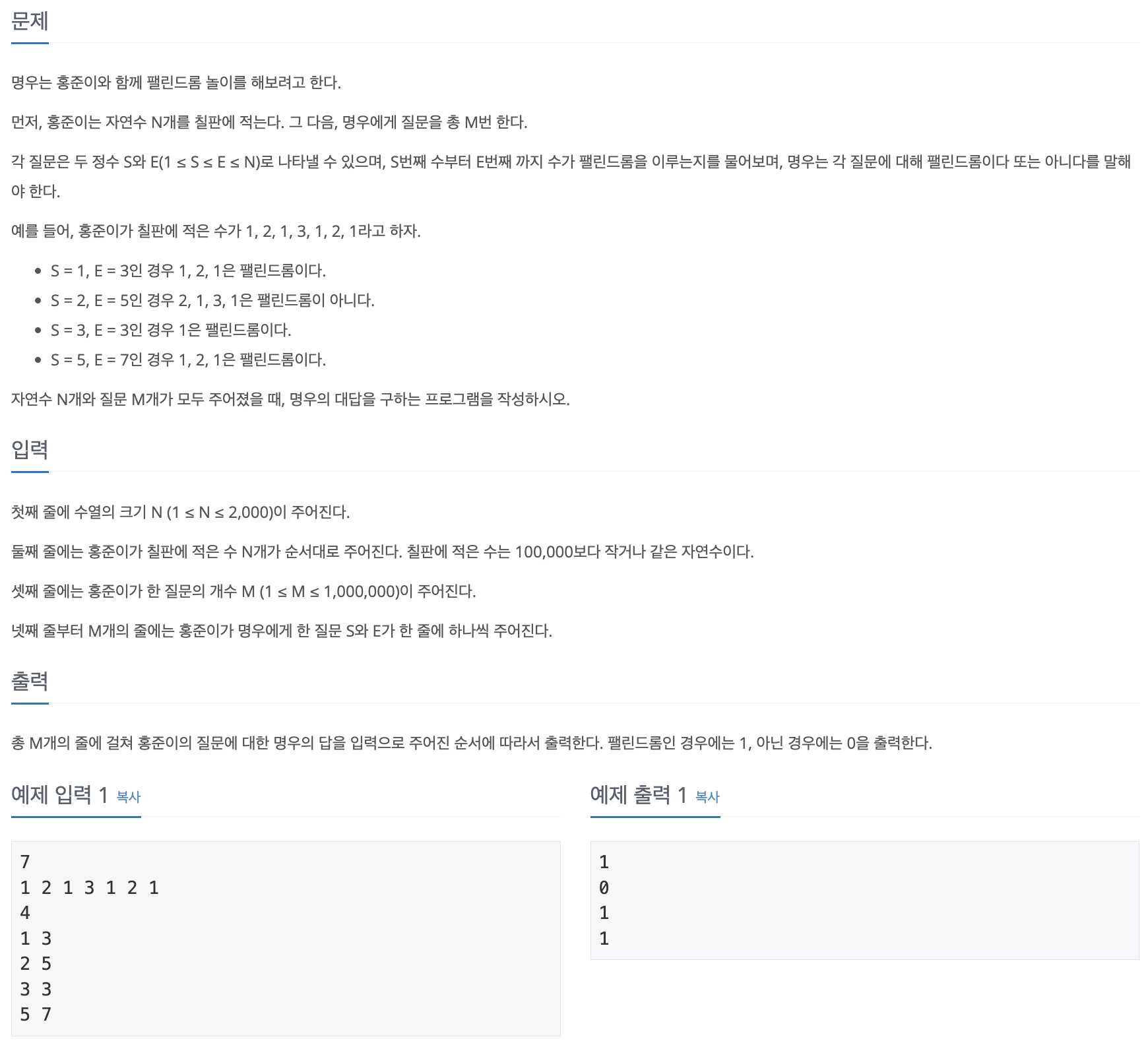
📝 답안
import sys
sys.setrecursionlimit(10 ** 9)
input = sys.stdin.readline
N = int(input().strip())
nums = list(map(int, input().strip().split()))
M = int(input().strip())
visited = [[0] * N for _ in range(N)]
def is_palindrome(s, e):
while s <= e:
if nums[s] == nums[e]:
if not visited[s][e]:
result = is_palindrome(s + 1, e - 1)
visited[s][e] = result
return visited[s][e]
else:
return 0
return 1
for _ in range(M):
s, e = map(int, input().strip().split())
print(is_palindrome(s - 1, e - 1))5. Longest Palindromic Substring
📄 문제

📝 답안
class Solution(object):
def longestPalindrome(self, s):
"""
:type s: str
:rtype: str
"""
n = len(s)
dp = [[None] * n for _ in range(n)]
for i in range(n):
dp[i][i] = True
longest_start, max_len = 0, 1
for end in range(n):
for start in reversed(range(end)):
if s[start] == s[end]:
if end - start == 1 or dp[start + 1][end - 1]:
dp[start][end] = True
if max_len < end - start + 1:
max_len = end - start + 1
longest_start = start
return s[longest_start:longest_start + max_len]
