✅ 할당기의 요건

명시적 메모리 할당기(Allocator)는 아래의 요건들을 충족해야 한다.

1. 임의의 요청 순서 처리하기

• 할당기는 메모리 할당 요청과 반환 요청이 어떤 순서로 들어올지 아무런 가정도 할 수 없다. 어떤 순서로 요청이 들어오든 간에 메모리 해제는 그에 대응되는 이전에 할당된 메모리 블록에 대해 이뤄져야 한다.

2. 요청에 즉시 응답하기

• 할당기는 요청에 즉시 응답해야 한다. 성능 향상을 위해 요청을 재정렬하거나 버퍼에 저장해두었다가 나중에 처리하려고 해서는 안 된다.

3. 힙만 사용하기

• 확장성을 갖기 위해 할당기에 의해 사용되는 non-scalar 자료구조들은 힙에 저장되어야 한다. (이때 non-scalar 자료구조란 배열, 트리, 그래프와 같이 단순한 값 형식이 아니라, 여러 개의 필드 또는 멤버 변수로 이루어진 객체나 자료구조를 의미한다.)

4. 블록 정렬하기

• 할당기는 어떤 타입의 데이터 객체도 저장할 수 있도록 블록을 정렬해야 한다.
• 리눅스에서 x86 머신의 경우 8-byte, x86-64 머신의 경우 16-byte 정렬을 사용한다.

5. 할당된 블록을 수정하지 않기

• 할당기는 free 상태의 블록만 조작하고 변경할 수 있다. 이미 할당된 블록에 대해서는 수정하거나 이동시킬 수 없다. 따라서 할당된 블록을 압축시키는 것과 같은 기법은 허용되지 않는다.

⛳️ 할당기의 목표

1️⃣ 처리량(Throughput) 극대화하기

여러 개의 할당 요청과 반환 요청이 들어올 때 단위 시간 당 완료되는 요청의 수를 최대화하는 것이다.

2️⃣ 메모리 이용도(Memory Utilization)를 최대화하기

힙을 얼마나 효율적으로 사용하고 있는지는 peak utilization을 통해 측정할 수 있다.

아래의 공식에서 k번의 메모리 할당 및 반환 요청이 들어왔다고 가정했을 때 P는 현재까지 할당된 블록들의 바이트 사이즈이고, H는 현재 힙의 사이즈를 나타낸다.

즉, peak utilization U는 brk 포인터를 고정해둔 상태에서 주어진 힙을 얼마나 알차게 잘 활용하고 있는지를 의미한다.

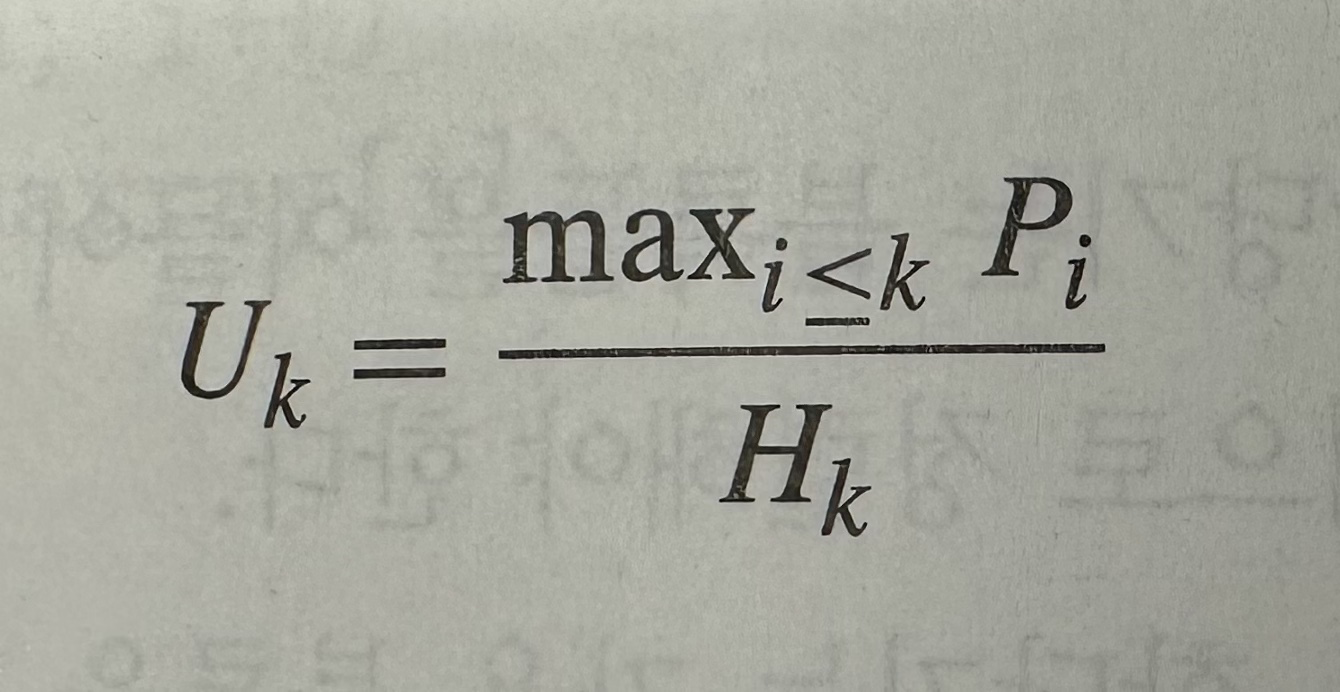
⚖️ 두 가지 목표 사이에서 균형 잡기

메모리 이용도를 높이려면 주어진 힙 사이즈 내에서 가용한 상태의 공간을 찾는 과정이 필요한데, 이 과정에서 발생한 오버헤드가 단위시간당 처리량을 낮출 수 있다.

이처럼 처리량과 메모리 이용도는 트레이드 오프 관계에 있기 때문에, 할당기를 설계할 때에는 이 두 가지 목표 사이에서 적절한 균형 지점을 찾는 것이 필요하다.

이를 위해선 아래의 이슈들을 고려해야 한다.

1️⃣ 가용 블록 구성 (Free Block Organization)

• 어떻게 가용 블록을 지속적으로 추적하는가?

2️⃣ 배치 (Placement)

• 새로 할당된 블록을 놓을 적절한 지점을 어떻게 찾는가?

3️⃣ 분할 (Splitting)

• 새로 할당된 블록을 가용한 블록에 배치한 후, 가용 블록의 남은 부분들로 무엇을 할 것인가?

4️⃣ 연결 (Coalescing)

• 방금 반환된 블록으로 무엇을 할 것인가?

메모리 블록을 어떻게 구성, 배치, 분할, 연결할 수 있을지에 대해서는 다음 절에서 자세히 살펴보자.

💡 묵시적 가용 리스트

🧱 힙 블록의 포맷

모든 할당기는 블록의 경계를 구분하고, 할당된 블록과 가용한 블록을 구분할 수 있는 자료 구조를 필요로 하는데, 대부분의 할당기에서는 이 정보를 블록 내에 저장한다.

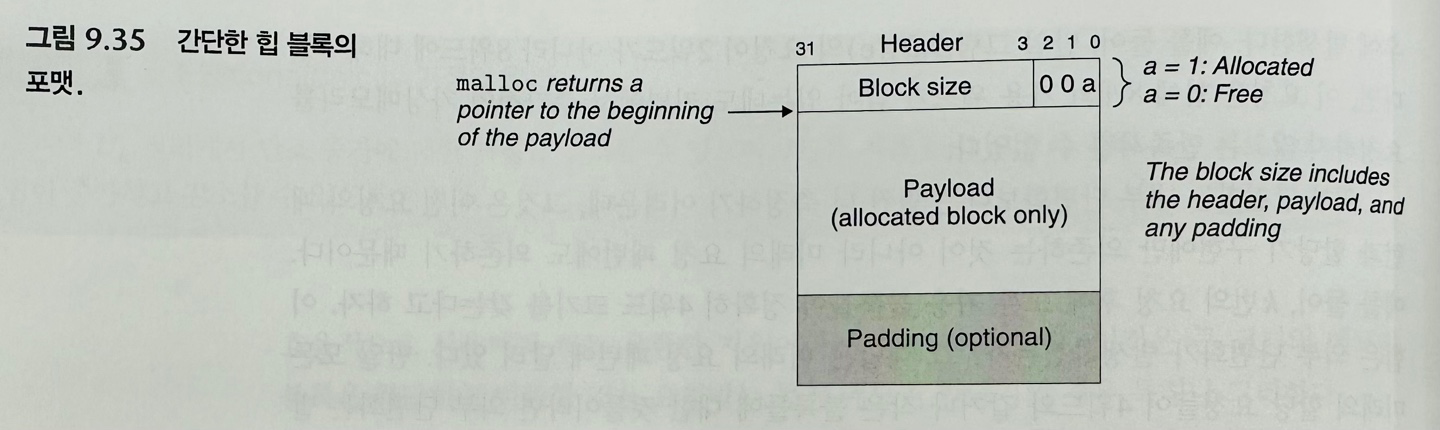
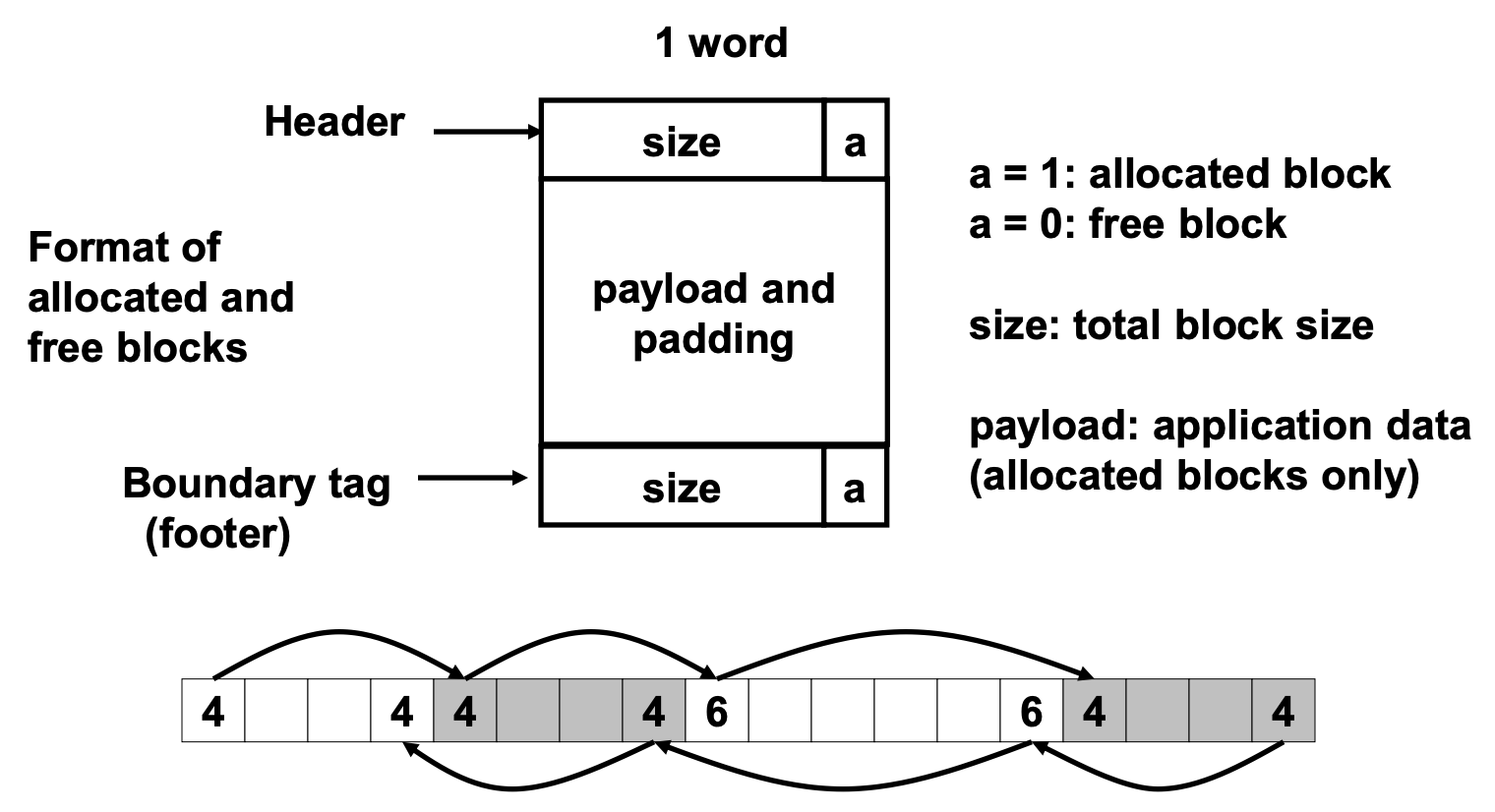
아래의 그림을 보면 한 블록은 1 워드 헤더, 데이터, 패딩(optional)으로 구성된다.

🤔 (참고) 워드란?
워드는 컴퓨터가 한 번에 처리할 수 있는 데이터의 비트 수를 나타낸다.
32-bit 아키텍처에서 1 워드는 32bit(4byte)이고, 64-bit 아키텍처에서 1 워드는 64bit(8byte)이다.

1️⃣ 헤더 (Header)

헤더는 블록의 크기(헤더와 패딩을 포함한)와 블록의 할당 여부 정보를 가지고 있다.

double-word alignment constraint를 부여한다면 블록의 크기는 항상 8의 배수이므로, 블록 크기의 하위 3비트는 항상 0이다.

따라서 헤더에서 블록의 크기를 표현하고 남는 3비트는 블록의 할당/가용 여부를 표현하는 데에 사용할 수 있다.

예컨대 블록 크기가 24 바이트(0x18)인 블록이 할당된 상태라면 헤더는 0x00000018 | 0x1 = 0x00000019와 같이 표현할 수 있고, 블록 크기가 40 바이트(0x28)인 블록이 가용한 상태라면 헤더는 0x00000018 | 0x0 = 0x00000028와 같이 표현할 수 있다.

2️⃣ 데이터 (Payload)

malloc이 리턴하는 것은 payload 영역의 시작점이다.

3️⃣ 패딩 (Padding)

패딩은 외부 단편화를 극복하기 위한 할당기 전략의 일부분으로서 들어갈 수 있고,또는 정렬 요구사항을 만족하기 위해 들어갈 수도 있다.

💡 묵시적 가용 리스트 (Implicit Free Lists)

📍 묵시적 가용 리스트란?

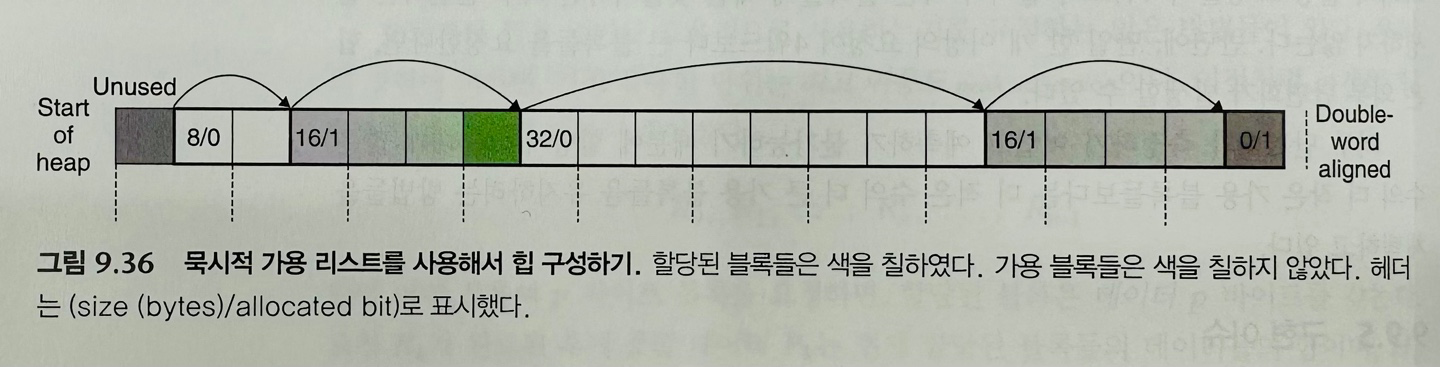
위의 힙 블록을 배열로 표현한 구조를 묵시적 가용 리스트라고 한다.

"묵시적(Implicit)"이라 표현하는 이유는 메모리 블록이 헤더 내 필드에 의해 암묵적으로 연결되기 때문이다.

앞서 살펴보았듯이 헤더 영역에는 블록의 크기와 할당 여부 정보가 있기 때문에 헤더 정보를 바탕으로 다음 메모리 블록의 위치를 파악할 수 있다.

📍 epilogue 블록

묵시적 가용 리스트의 마지막에는 할당기가 리스트의 끝 지점에 도달했다는 것을 알려주기 위한 epilogue 블록이 있다.

이 eqilogue 블록에는 할당 비트(allocated bit)가 셋팅되어 있어 항상 할당된 상태로 표시되어 있고, 사이즈는 0 바이트이다.

📍 묵시적 가용 리스트의 장단점

묵시적 가용 리스트는 구조가 단순하다는 장점이 있지만, 성능과 효율성 측면에서 단점도 존재한다.

묵시적 가용 리스트는 모든 블록을 순차적으로 검색하여 필요한 크기의 빈 공간을 찾는데, 만약 가용한 공간이 리스트의 마지막에 있다면 그 공간을 찾기 위해 전체 리스트를 순회해야 하므로 시간 복잡도가 O(n)이 된다.

그리고 묵시적 가용 리스트는 메모리 단편화의 가능성이 높은데, 이는 힙 블록의 포맷과 시스템의 정렬 요구 조건과 관련이 있다.

우선 각 힙 블록마다 헤더와 Optional 푸터가 추가됨에 따라 오버헤드가 발생하여 내부 단편화가 발생할 수 있다.

그리고 정렬 조건으로서 double word alignment를 사용하는 경우 64비트 머신에서 최소 블록 크기는 16바이트이기 때문에, 애플리케이션이 1 바이트를 요청할지라도 16바이트의 메모리 블록이 할당되어 내부 단편화가 발생할 수 있다.

💡 할당한 블록의 배치

애플리케이션이 k 바이트의 블록을 요청하면 할당기는 요청한 블록을 저장하기에 충분히 큰 가용 블록을 리스트에서 검색한다.

이 검색을 수행하는 방법은 배치 정책에 의해 결정되는데, first fit, next fit, best fit 정책이 주로 사용된다.

1️⃣ first fit

first fit 정책은 메모리를 순차적으로 검색하여 요구 사항을 충족하는 첫 번째 자유 공간 블록에 데이터를 할당하는 방식이다.

first fit 정책의 장점은 리스트의 마지막에 가장 큰 가용 블록들을 남겨두는 경향이 있다는 것이고, 단점은 리스트의 앞부분에 작은 가용 블록들을 남겨두는 경향이 있어서 큰 블록을 찾는 경우에 검색시간이 늘어난다는 점이다.

2️⃣ next fit

next fit 정책은 first fit 정책과 유사하지만, 메모리 검색을 이전에 종료된 지점에서부터 시작한다는 차이가 있다.

리스트의 앞부분이 작은 크기의 메모리 조각들로 구성되면 next fit은 first fit에 비해 매우 빠른 속도를 가지지만, 몇몇 연구 결과에 의하면 next fit이 first fit보다 최악의 메모리 이용도를 갖는 것으로 밝혀졌다.

3️⃣ best fit

best fit 정책은 요구 사항을 충족하는 모든 가용 블록 중에서 가장 작은 블록에 데이터를 할당한다.

이 방식은 내부 단편화를 최소화할 수 있지만, 메모리의 모든 부분을 검색해야 하므로 비용이 많이 들 수 있다.

💡 가용 블록의 분할

할당기가 적합한 크기의 가용 블록을 찾으면 어느 정도의 메모리 블록을 할당할지 결정해야 한다.

대부분의 경우 가용한 블록 전체를 사용하기 보다 일부분만 할당하여 사용한다.

💡 가용 블록 연결하기

할당기가 할당한 블록을 반환했을 때, 반환된 블록 근처에 다른 가용한 블록들이 있을 수 있다.

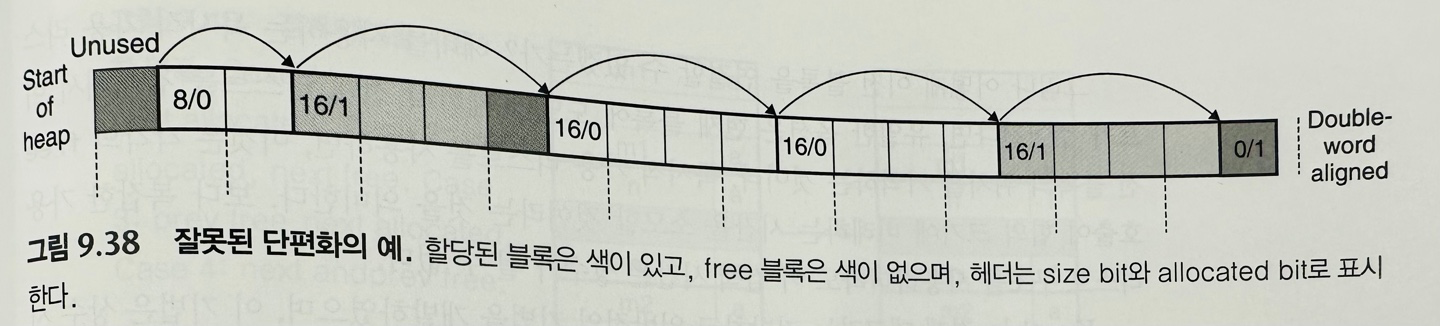
이렇게 가용한 블록들이 쪼개져 있으면 오류 단편화(false fragmentation)을 야기할 수 있다. 즉, 전체적으로 봤을 때 가용한 블록이 충분히 큼에도 불구하고 쪼개어져 있어서 메모리 할당에 실패하는 것이다.

이러한 오류 단편화를 극복하기 위해선 연결(coalescing) 과정을 통해서 인접해있는 가용 블록들을 통합해야 한다.

블록이 반환될 때마다 인접 블록을 통합하는 즉시 연결(immediate coalescing) 방법을 사용할 수도 있고, 일정 시간 후(ex. 할당 요청이 실패했을 때)에 통합하는 지연 연결(deferred coalescing) 방법을 사용할 수도 있다.

즉시 연결 방법의 경우 간단하고 상수시간 내에 수행될 수 있지만 경우에 따라 블록이 통합되었다가 다시 분할되는 thrashing 상태를 야기할 수 있다. 따라서 속도가 빠른 할당기들은 지연 연결 방법을 사용하는 경우가 많다.

🔗 경계 태그(Boundary Tags)로 연결하기

가용 블록은 어떻게 연결할 수 있을까? 우선 블록의 헤더에 블록의 사이즈 정보가 있기 때문에 그 사이즈만큼 이동해서 다음 블록을 찾고 연결할 수 있을 것이다.

그렇다면 이전 블록은 어떻게 연결할 수 있을까? 앞서 살펴본 헤더를 사용하는 묵시적 가용 리스트라면 반환하려는 블록에 도달할 때까지 전체 리스트를 검색해서 이전 블록의 위치를 기억해야 하므로 시간복잡도가 O(N)이 될 것이다.

이전 블록의 위치를 찾을 수 있도록 Knuth는 경계 태그(Boundary Tags)라는 기법을 개발하였는데, 바로 각 블록의 끝부분에 헤더를 복사한 푸터(경계 태그)를 추가해주는 방법이다.

아래의 그림처럼 푸터의 정보를 보고 이전 블록의 위치로 거슬러 올라갈 수 있기 때문에, 상수시간에 이전 블록을 연결할 수 있게 된다.

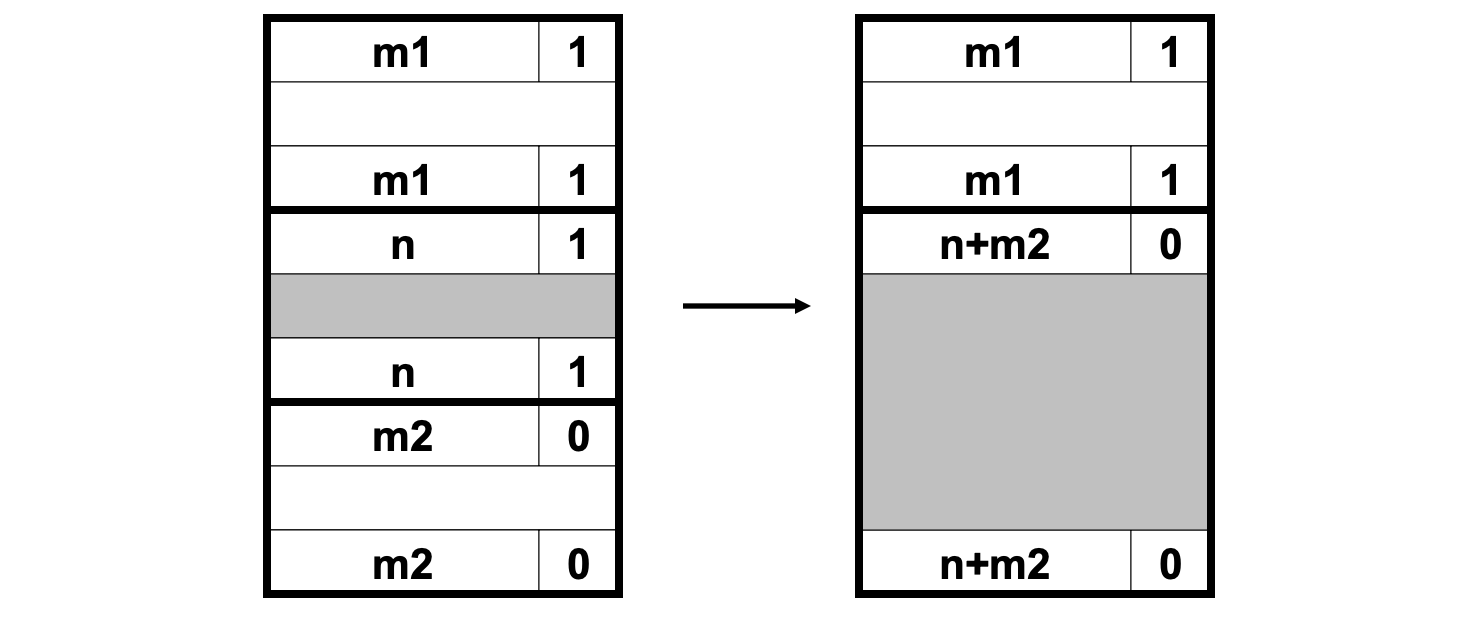
아래의 예시를 살펴보면 사이즈가 n인 블록이 해제되면서 n 블록과 m2 블록이 연결되고, 헤더와 푸터의 사이즈 정보는 n+m2로 변경된다.

다만 경계 태그에도 한계점이 존재한다. 만약 작은 메모리 블록을 많이 다뤄야 하는 애플리케이션이라면 각각의 메모리 블록에 있는 헤더와 푸터가 메모리 오버헤드를 야기할 수 있다.