[JS / 알고리즘] binaryHeap 이진힙

드림보이즈·2023년 3월 3일
알고리즘

문제

정수를 요소로 갖는 배열을 입력받아 이진 힙(binary heap)*을 리턴하라.

  • 이진 힙(binary heap)은 노드의 값이 특정한 순서를 가지고 있는 완전 이진 트리(Complete Binary Tree)입니다.

  • 완전 이진 트리는 이진 트리의 (마지막 레벨 또는 마지막 깊이를 제외하고) 모든 레벨이 노드로 가득 채워져 있어야 합니다. 마지막 레벨은 왼쪽부터 차례대로 채워져 있습니다.

  • 이진 힙에서 부모 노드의 값이 (이진 트리이므로 2개의) 자식 노드의 값보다 큰 경우를 최대 힙(max heap), 반대의 경우를 최소 힙(min heap)이라고 합니다.

주의사항

  • 최대 힙(max heap)을 구현해야 합니다.

  • 입력으로 주어진 배열은 중첩되지 않은 1차원 배열입니다.

  • 최대 힙 구현을 위해 선언된 함수들(getParentIdx, insert)을 전부 완성해야 합니다.

  • swap, getParentIdx, insert를 전부 사용해야 합니다.

  • swap, binaryHeap을 수정하지 않아야 합니다.

  • 테스트 케이스에서 힙 함수들을 정확히 구현했는지 함께 테스트합니다.

  • insert의 시간 복잡도는 O(logN)입니다.

  • 주어진 배열을 내림차순으로 정렬(O(logN))해도 최대 힙의 조건을 만족합니다. 하지만 이는 insert를 구현하는 것과는 거리가 먼 방법이며, 테스트를 통과할 수도 없습니다.

예시

let output = binaryHeap([5, 4, 3, 2, 1]);
console.log(output); // --> [5, 4, 3, 2, 1]

output = binaryHeap([3, 1, 21]);
console.log(output); // --> [21, 1, 3]

output = binaryHeap([4, 10, 3, 5, 1]);
console.log(output); // --> [10, 5, 3, 4, 1]

힌트

이진 힙은 '트리 객체' or '배열'로 구현 가능

배열로 구현시

거의 모든 트리를 배열로 구현 가능

저장공간 절약 + 노드 접근 시 오버헤드(반복,재귀) 줄어듬

매우 복잡한 인덱스 관리 필요

트리 객체로 구현시

직관적(이해하기 쉬움)

대신 저장공간과 오버헤드 희생해야

모든 기술은 다수의 선택 사이의 Trade-Off 다!

완전 이진 트리는 노드가 낮은 레벨부터 채워지고, 같은 레벨에서는 왼쪽부터 채워지기에 배열이 더 좋다!

최대 힙과 이진 검색 트리는 완전이진트리지만, 최대 힙은 부모와 자식간의 관계만 유지하고, 이진 검색 트리는 모든 노드가 정렬된다.

뭐가 이리 길고 내용이 많냐?

들어가기 전에...

(참고: https://kayuse88.github.io/binary-heap/)

힙(Heap)

트리 기반 자료구조로, 힙 속성을 만족하는 거의 완전한 트리.

힙 속성 : 최대 힙일 경우, 부모 노드는 반드시 자식 노드보다 커야 한다, 따라서 최상위 노드는 최대값 가진다

우선 순위 큐 구현하는데 적합

부모-자식 관계만 정의되어 있지 형제(같은 레벨)의 우선순위 없음

이진 힙 (binaryHeap)

힙 중에서 가장 널리 쓰이며 이진 트리 형태의 힙

마지막 레벨은 왼쪽부터 차 있어야 하고, 그 외 모든 레벨의 노드가 채워져 있어야 한다.

이진 힙의 삽입 과정(Insert)

  1. 요소를 가장 마지막 노드에 추가

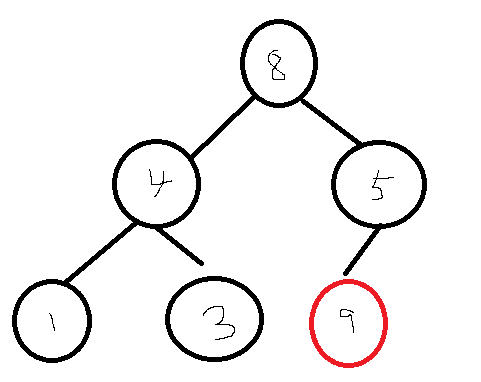
  2. 추가한 요소를 부모와 비교하고, 순서가 힙 조건과 일치한다면 중지, 일치 안 하면 부모와 위치 교환, 일치 할 때 까지 반복.

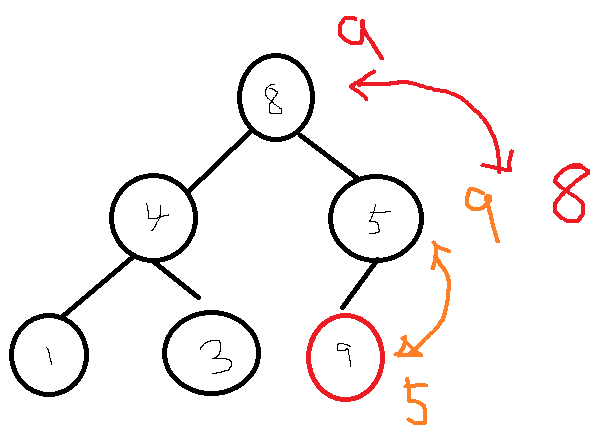
이진 힙 삭제 과정(Delete)

루트 노드는 최소값 혹은 최대값을 가질테고, 탐색할 때 걸리는 시간은 항상 O(1)이겠지. 값을 추출하고 다음 값을 루트로 만드는 작업을 다운힙이라고 한다.

  1. 루트 노드 삭제
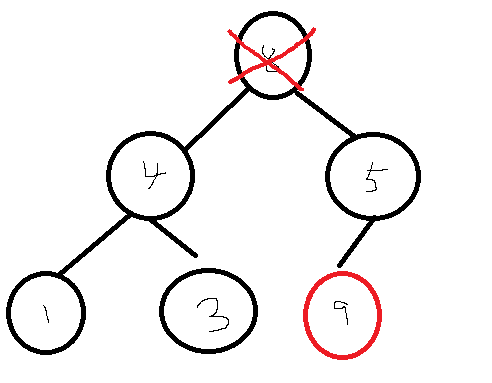
  2. 마지막 노드를 루트로 이동, 루트를 자식 노드와 비교. 힙 조건을 일치할 때 까지 교환

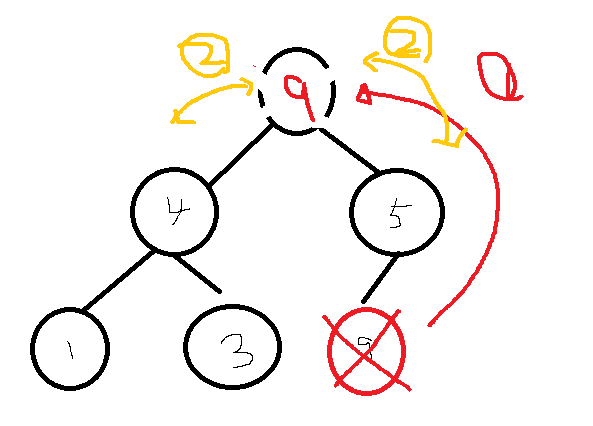
위 내용을 종합해 볼 때

- 부모 _ 자식 간의 "교환"

- 특정 자식의 "부모 인덱스를 찾기"

두 기능이 꼭 필요함을 알 수 있다.

핵심 포인트

0. 이 문제는 최대 힙이다. 부모가 젤 커야돼.

1.배열의 두 요소 간의 swap 함수

3가지 방법을 소개한다. 모두 알아두자.


function swap(idx1, idx2, arr) {
	//1.임시 변수 활용
	//let temp = arr[idx1];
	//arr[idx1] = arr[idx2];
	//arr[idx2] = temp;

	//2.Destructuring assignment 활용
	//arr이 refernece type이라 가능
	[arr[idx2], arr[idx1]] = [arr[idx1], arr[idx2]];

	//3. XOR 연산 활용
	// arr[idx1] ^= arr[idx2];
	// arr[idx2] ^= arr[idx1];
	// arr[idx1] ^= arr[idx2];

1번은 간단하니 패스

2번의

구조 분해 할당(Destructuring assignment)?

(참고: https://ko.javascript.info/destructuring-assignment)

객체와 배열은 자바스크립트에서 가장 많이 쓰이는 자료 구조

키를 가진 데이터 여러 개를 하나의 엔티티에 저장할 땐 객체를,
컬렉션에 데이터를 순서대로 저장할 땐 배열을 사용

개발을 하다 보면 함수에 객체나 배열을 전달해야 하는 경우가 생기곤 합니다. 가끔은 객체나 배열에 저장된 데이터 전체가 아닌 일부만 필요한 경우가 생기기도 하죠.

이럴 때 객체나 배열을 변수로 '분해’할 수 있게 해주는 특별한 문법인 구조 분해 할당(destructuring assignment) 을 사용할 수 있습니다...(중략)

결국 핵심은 객체, 배열을 변수로 '분해'할 수 있단 뜻이다. 

[arr[idx2], arr[idx1]] = [arr[idx1], arr[idx2]];

언뜻보면 두 요소의 순서를 바꿔주는 것 같지만,
사실 arr 배열의 두 요소를 가져와 서로의 값으로 변경해주는 것이다.
(같은 말인가? 뭐 어쨋든)

계속 하자.

3번의 XOR 연산 활용은 또 뭔소리야?

XOR 연산

같은 위치에 있는 비트 값이 동일하면 0, 다르면 1이 되는 연산자

예를 들어 3과 7을 비교해보면, 이진수로 3은 11, 7은 111이다.

// 11 = 3
//111 = 7
----
//100 = 4가 나온다

재밌는 점은 3에 동일한 값을 2번 xor 연산하면 본래 값으로 돌아온다는 것


//100 = 4
//111 = 7
---
//011 = 3

이를 이용해 추가적인 변수 선언(1번처럼 임시 변수 이용)없이 서로 값을 바꿀 수 있다.

let a = 3;
let b = 7;
a = a ^ b; //3 ^ 7 = 4
b = b ^ a; //7 ^ 4 = 3
a = a ^ b; //4 ^ 3 = 7
// a = 7, b = 3;

2. 부모 노드 인덱스 찾기 함수

정렬되지 않은 배열이 들어왔을 때, 정렬을 하려면 각 자식 노드이 자기 부모와 크기 비교를 해야할텐데, 내 부모가 몇 번째 인덱스에 있는지 어떻게 찾을래?

이건 솔직히 공식을 외워도 되지만, 우린 학생이니까 노가다로 공식을 이끌어 내보자.

다행히 "이진" 트리라 찾아내기 더 쉬울 거야.

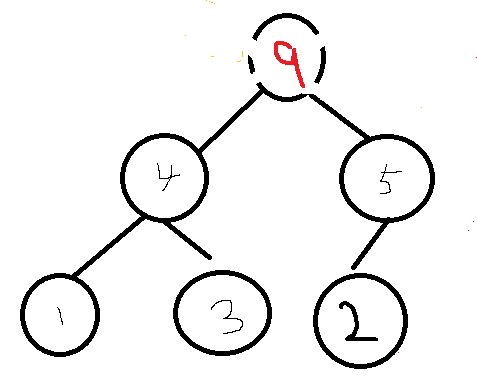
요건 트리를 이해하기 편하게 트리화 한거고,
배열로 [9,4,5,1,3,2] 이렇게 올 것이다.

여기서 4, 인덱스 1의 부모는 9, 인덱스 0이다.
5, 인덱스 2의 부모는 9, 인덱스 0이다.

음... 아직 감이 안와

1, 인덱스 3의 부모는 4, 인덱스 1이다.
3, 인덱스 4의 부모는 4, 인덱스 1이다.

자 인덱스만 때놓고 보자. Like IQ 테스트

1 > 0
2 > 0

3 > 1
4 > 1

5 > 2
6 > 2

7 > 3
8 > 3
9 > 3
10 > 3


요런 참새 나도 모르겠다

(자식 인덱스 -1 / 2) 의 반내림 값 = 부모 인덱스

이다. 해시 함수도 아니고 이렇게 보니까 알겠네.

function getParentIdx(idx) {
return Math.floor((idx - 1) / 2);
}

3. Insert(삽입) 함수

위에서 방금 봤잖아, 삽입 과정은?
일단 맨 끝에 넣고 > 부모와 비교 > 일치 않으면 계속 바꿔

function insert(heap, item) {
  // 일단 끝에 넣어
  heap.push(item);
  // 부모와 비교해서 크면 바꾸고, 그렇게 쭉 맨위까지 해봐
  let curIdx = heap.length - 1;
  let parIdx = getParentIdx(curIdx);
  
  // 부모 인덱스가 0 이상(루트) && 자식이 더 크면
  while(pIdx >=0 && heap[curIdx] > heap[parIdx]) {
  	// 바꿔
  	swap(curIdx, parIdx, heap);
  	// 자식, 부모 인덱스도 바꿔줘야 그 위랑 비교하지
  	curIdx = parIdx;
  	parIdx = getParentIdx(curIdx);
  }
  return heap;
  }

4. binaryHeap 구현 함수

밀키트다. 다 준비해놨다. 레시피 대로 끓이기만 해.

정리되지 않은 배열을 받을 거고,

요소 하나 하나씩, 그리고 누적이 필요하니까 reduce를 사용해서

insert 함수 이용해서 넣기만 하면 돼.

function binaryHeap(arr) {
return arr.reduce((heap,item) => (
	return insert(heap,item);
},[])
};

끝, 참 쉽죠?

전체 코드

// 두 변수를 바꾸는 방법
function swap(idx1, idx2, arr) {
// 1. 임시 변수 활용
// let temp = idx1;
// arr[idx1] = arr[idx2];
// arr[idx2] = temp;

// 2. Destructuring assignment를 활용한 방법
// arr이 reference type이라 가능
[arr[idx1], arr[idx2]] = [arr[idx2], arr[idx1]];

// 3. XOR 연산을 활용한 방법
// arr[idx1] ^= arr[idx2];
// arr[idx2] ^= arr[idx1];
// arr[idx1] ^= arr[idx2];
}

function getParentIdx(idx) {
return Math.floor((idx - 1) / 2);
}

function insert(heap, item) {
// 일단 item을 끝에 넣어
heap.push(item);
// item 부모와 크기 비교해서 크면 바꾸고, 그렇게 맨 위까지 해봐
let curIdx = heap.length - 1;
let pIdx = getParentIdx(curIdx);
while (pIdx >= 0 && heap[curIdx] > heap[pIdx]) {
  swap(curIdx, pIdx, heap);
  // 바뀌면 그 위 놈이랑 비교해야 하니까 세팅 다시 해줘야지
  curIdx = pIdx;
  pIdx = getParentIdx(curIdx);
}
return heap;
}

const binaryHeap = function (arr) {
return arr.reduce((heap, item) => {
  return insert(heap, item);
}, []);
};
profile
드림보이즈
시리즈 클릭하셔서 카테고리 별로 편하게 보세용
이전 포스트

[감정일기] 코드 스테이츠 블록체인 부트캠프 8기 DAY-68 감정일기

다음 포스트

[MIT: BlockChain & Money] 4. Blockchain basics & Consensus 정리

0개의 댓글