학습 계기
블록체인 지갑을 만들기 위한 초 기본 개념.
사전 지식
암호화폐 지갑 분류 1 : 인터넷 연결 유무에 따라
- Hot 월렛 : 온라인
- 웹 (확장 프로그램, 웹 사이트)
-데스크톱 (인터넷 접속 여부 따라 핫, 콜드 둘다 가능)
-모바일 (인터넷 접속 여부따라 핫, 콜드 둘다 가능) - Cold 월렛 : 오프라인
- 페이퍼
-하드웨어
암호화폐 지갑 분류 2 : 키를 생성하는 방식에 따라
- 비결정적 월렛 : 매번 개인키를 '무작위'로 생성
- 결정적 월렛 : 시드키를 통해 개인키를 생성 (이미 어떤 값을 가질지 결정되어 있음)
BIP : Bitcoin Imrovement Proposal
1. BIP-32
주제 : HD 월렛 형식, 구축
HD 월렛
Hierarchial Deterministic Wallet = 계층적 결정적 지갑
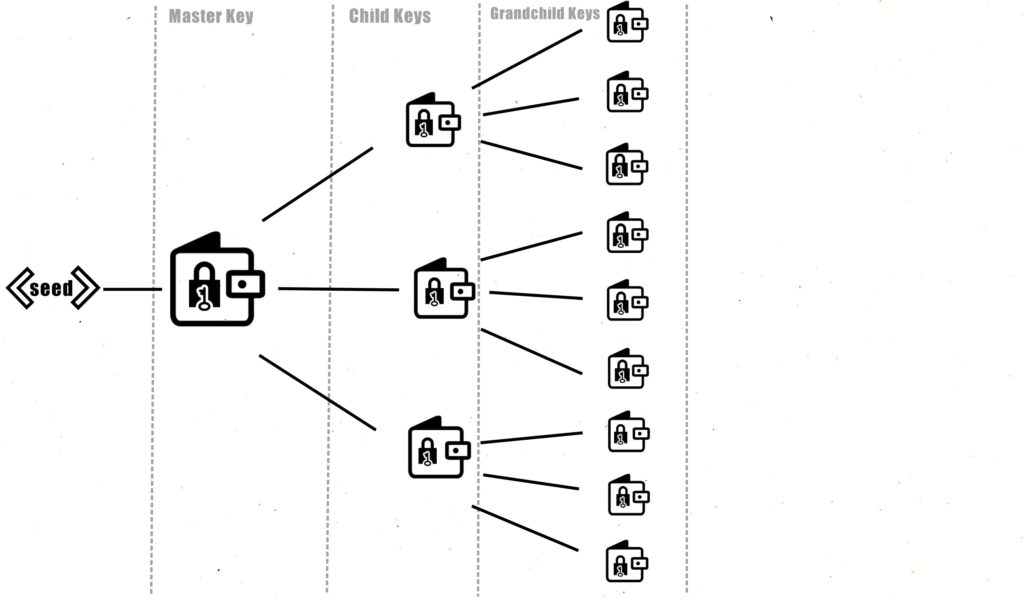
배경 : 하나보다 여러 주소를 사용하는 것이 더 안전하다!
'계란을 한 바구니에 담지 말라'는 말과 비슷하다.
하나의 지갑 주소로 모든 트랜잭션을 처리하다보면 보안적으로 위험에 노출될 가능성이 있다.
비트코인 트랜잭션 정보는 투명하다.
"누가 누구에게 언제 얼마를 보냈는지"를 모두가 볼 수 있다.
다만, '누가', '누구'가 지갑 주소로 나타날 뿐이다.
특정 지갑 주소에서 큰 액수의 코인들이 이동이 발견된다면?
검은 조직의 타케트가 될 수 있겠다.
결론적으로,
'비트코인 주소를 여러 개 사용하는 것이 좋을텐데,
어떻게 하면 사용자가 관리하기 편하면서 + 많은 주소 생성이 가능할까?'
에 대한 해답이 HD 월렛인 것이다.
구조
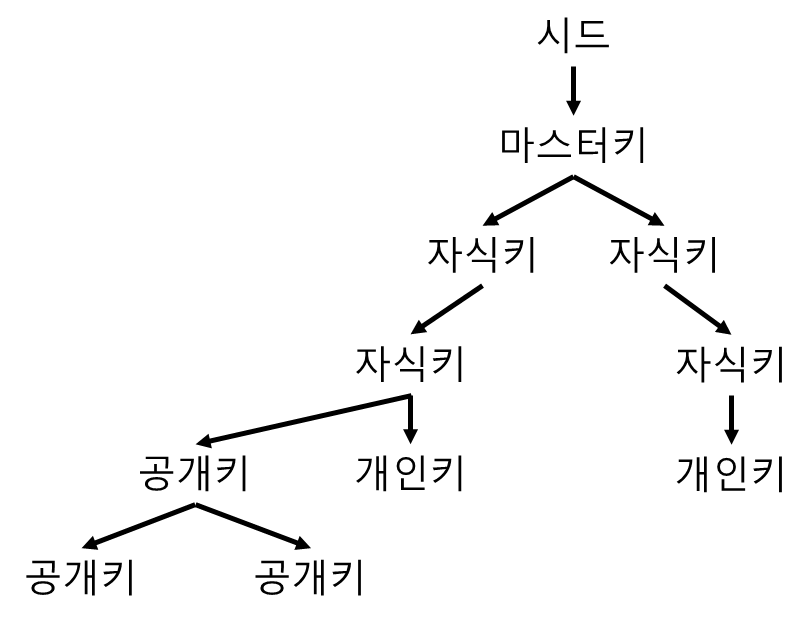
위처럼
시드를 통해 마스터키를, 마스터 키를 통해 자식 키들을 만든다. 따라서 계층적이며,
부모를 알면 자식을 알아낼 수 있기에 결정적이라고 하는 것이다.
구현
지금까지의 개념 설명으로
'아 ~ 그런갑다'
정도의 이해는 초등학생도 한다.
당신이 돈을 받고 일하는 프로라면, 혹은 프로가 되고 싶다면,
(내 자신에게 하는 이야기다 하...)
시드를 통해 마스터키를, 마스터 키를 통해 자식 키들을 만든다.
부모를 알면 자식을 알아낼 수 있기에 ~
에서
'어떻게 만드는데? 어떻게 알아내는데 ?'
라는 생각이 들어야만 한다.
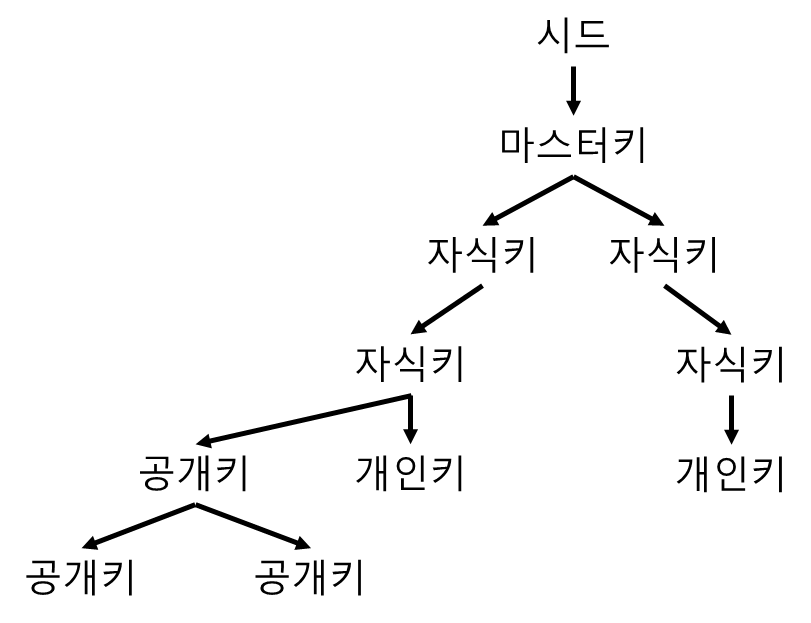
1. 시드 (마스터 시드)
먼저 시드를 만들어야 한다.
HD 월렛은
난수 => 니모닉 => 시드
순서로 생성된다.
1-1. 안전한 난수 생성기로 난수 생성
컴퓨터도 결국 기계다. 패턴이 존재한다.
컴퓨터가 만든 난수는 정말 예측 불가능한 랜덤인걸까?
더 안전한 난수를 만들기 위해, 난수를 만들고 해시 함수를 돌린 값을 사용한다던지(DBRG),
추가적인 작업을 통해 안전한 난수를 생성한다.
1-2. 니모닉
니모닉 : BIP-39에서 제안된, 결정적 지갑에서 난수를 12개 영단어로 인코딩한 그룹
본래는
난수 => 시드
로 시드를 생성한다. 이 시드만 적어 놓으면 내 모든 주소들을 찾을 수 있을 것이다.
굳이 왜 니모닉을 중간에 넣어야 하는가?
9e8ead3d61a74fe6a4ce542cb727660d
9e8ead3d61a74fe6a4ce542cb727560d
둘이 어디가 다른가? 이걸 종이에 적겠는가? 외울 수 있는가? 안 틀리고 쓸 자신 있는가?
아니면
apple banana cherry dog elephant...
가 기억하고 쓰기 편한가?
인간 입장에서 관리의 편리함을 위해
니모닉을 구현한 것이다.
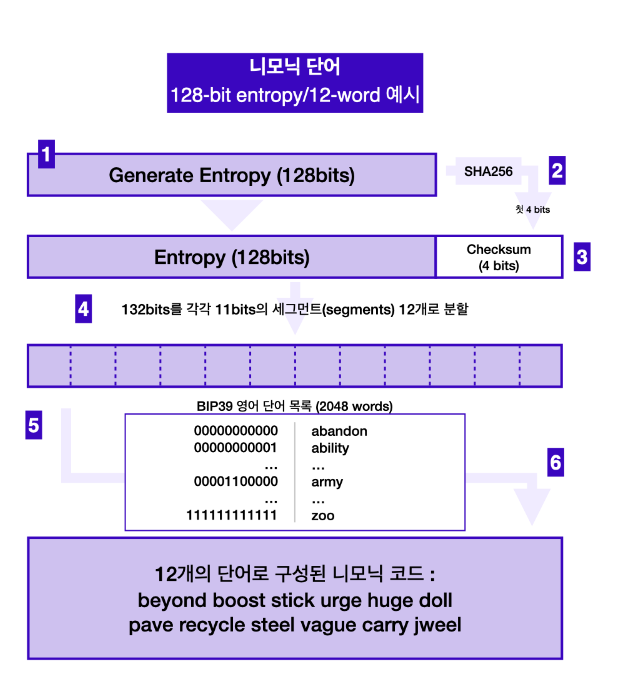
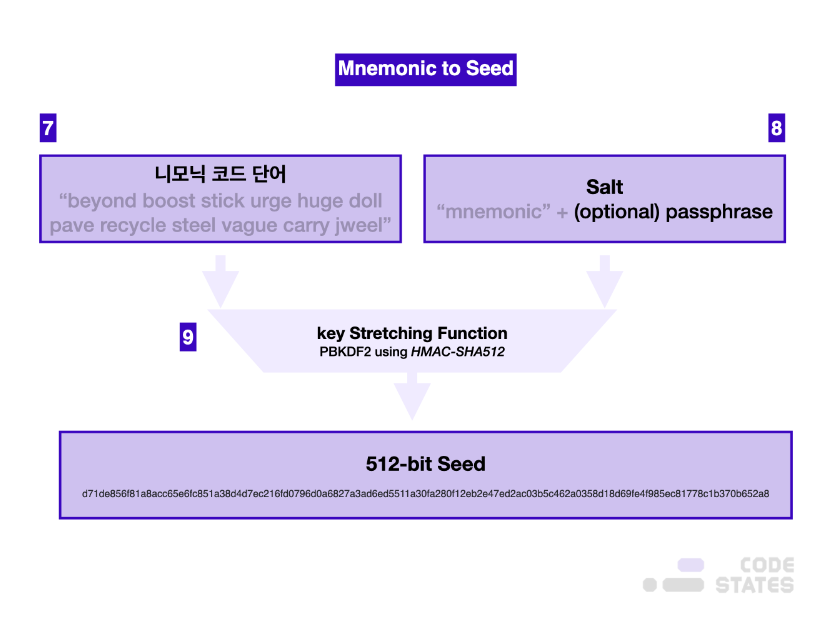
다음과 같은 순서로
난수 => 니모닉 => 시드
512비트 시드를 만들었다.
2. 마스터 키 (마스터 노드)
이제 시드를 통해 마스터 키를 만들어야 한다.
어떻게 ?
HMAC-SHA512 로
(물론 위 그림은 HMAC-SHA1 플로우다. 그냥 그런갑다 하고 넘어가자 우리가 암호학자도 아니고)
다만 HMAC-SHA512에 들어가는 Input이 2개인 점은 인지하고 가자.
마스터키를 만드는데 들어가는 Input은
'Bitcoin seed'(문자열) , 시드
이다.
(BIP-32에서 정한 문자열 고정값이다.)
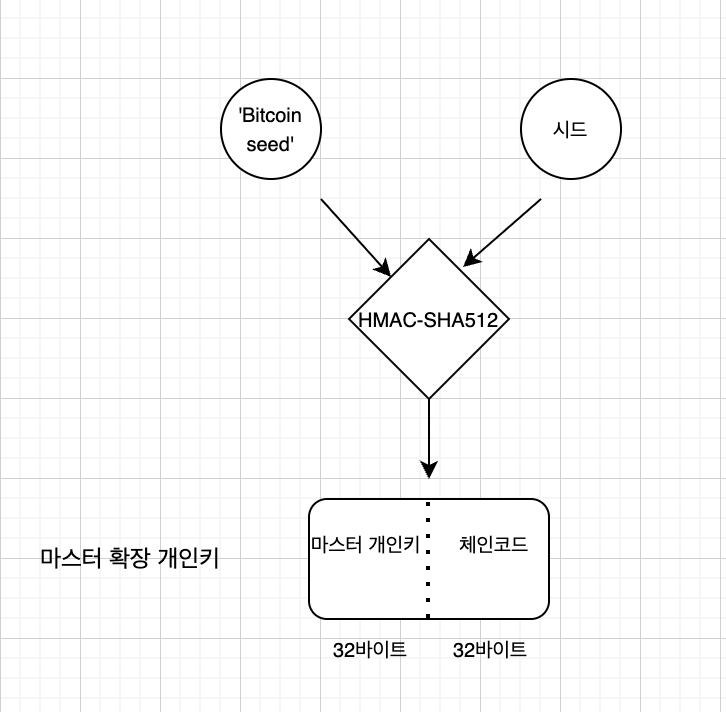
결과의 앞 절반 32 바이트는 마스터 개인키 (마스터 키),
뒤 절반 32바이트는 체인코드 라 하며
둘을 합친 값을 마스터 확장 개인키라 한다.
이렇게 마스터키를 구했다.
(마스터키 = 마스터 확장 개인키라고 생각하는 것이 편할 듯 싶다. 마스터 개인키와 체인코드 둘 다 이용하여 자식을 생성하기 때문이다.)
3. 자식키 생성
엔드게임(마지막 단계)다. 힘내자.
마스터키 => 자식키 과정이나
자식 키 => 자식의 자식 키 과정이 같다.
2단계만 더 하면 된다.
여기서 잠깐, 혹시
'왜 개인키만 그림? 공개키는 신경 안씀?'
라는 의문이 들었다면, 정신차리자.
개인키로 공개키를 타원곡선암호학으로 생성하니까. 언급 안해도 탁탁 좀 알아듣자.
BIP-32에서는 마스터키 => 자식키 생성 방법 2가지를 제안하고,
개발자가 선택해서 상황에 맞게 사용하라고 한다.
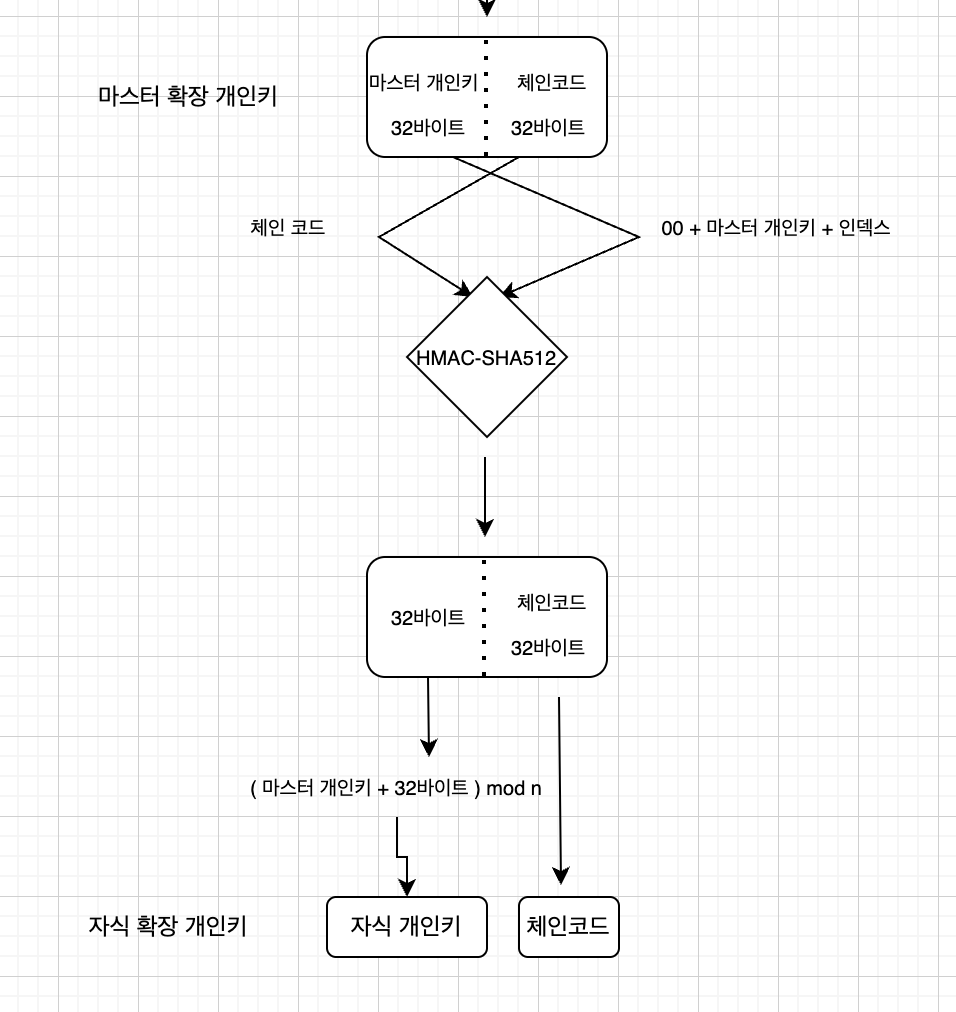
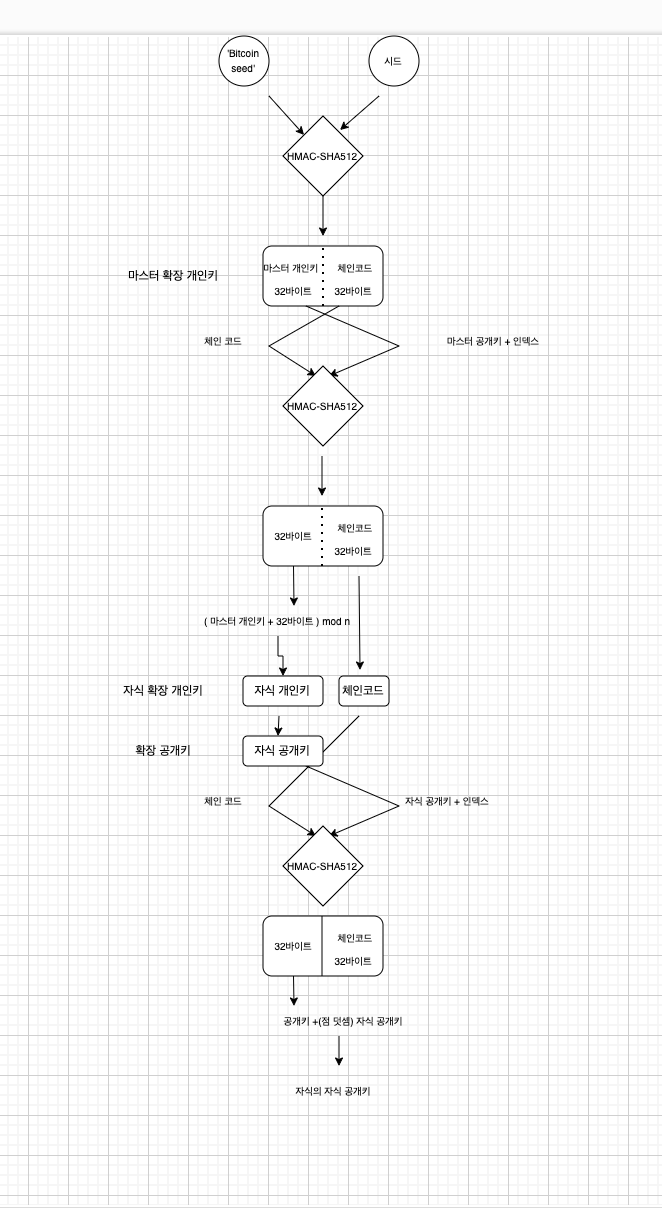
3-1. 강화 자식 키 (Hardened Child Key)
- 자식 키는 부모 키를 통해 만들어지지만, 부모 키가 노출되더라도 자식 키를 추적하기 어렵게 함
- 높은 보안이 필요한 경우 (금융 등)
부모의 비밀키를 이용해 자식키를 생성한다.
(일반은 부모의 공개키를 이용하기 때문에 보안이 덜 한것임)
역시 HMAC-SHA512 사용한다. 두 인자가 뭐냐고?
- 체인코드
- 00 + 부모 개인키 + 인덱스
인덱스 : 4바이트 길이의 정수
- 주소 관리를 위해 연속 증가 값을 넣을 수도
- 임의로 랜덤 인덱스를 넣을 수도
다시 HMAC-SHA512 결과값을 반으로 갈라서
- 뒤 32바이트 : 체인코드
- (부모 개인 키 + 앞 32바이트 ) mod n : 자식 개인키
mod n : n으로 나눈 나머지
n : secp256k1에서 정의된 값 사용 (고정됨)
secp256k1 : 타원 곡선 암호학에서 사용되는 특정 타원 곡선의 매개변수를 나타내는 표준 (특정한 타원 곡선인 y2 = x3 + 7)
이해하기 편하게 그림으로 보자.
3-2. 일반 자식 키 (Normal Child Key)
- 부모의 공개키를 통해 자식키를 생성
역시 HMAC-SHA512 사용한다. 두 인자는
- 체인코드
- 부모 공개키 + 인덱스
이며, 강화 자식 키 처럼
(부모 개인키 + 앞 32바이트 ) mod n으로 자식 개인키를 생성한다.
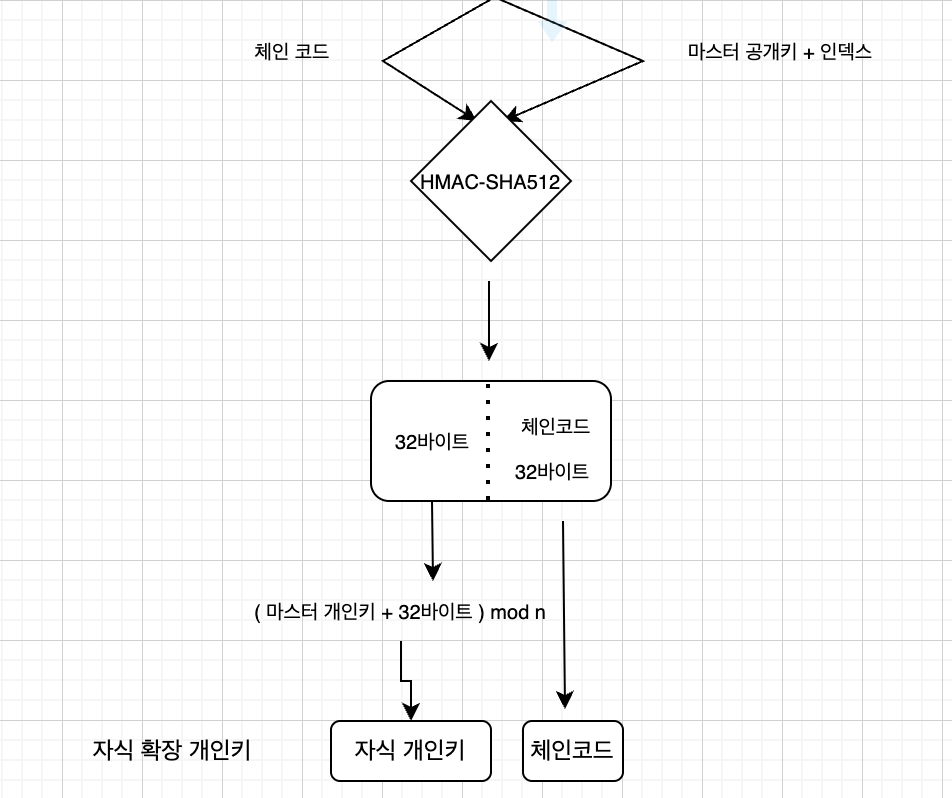
강화 자식 키 방법이랑 비슷하지만,
- 부모 공개키 사용
- 앞에 00 없음
차이가 있다.
이렇게 구한 자식 개인키로 일반 자식 공개키를 구할 수 있을텐데,
이 일반 자식 공개키를 확장 공개키라 부를 수 있고,
이걸로 자식 공개키를 만들 수 있다.
역시 HMAC-SHA512 사용한다. 두 인자는
- 체인코드
- 부모 공개키 + 인덱스
사용하고,
뒤 32 바이트를 체인코드로 사용하는 것은 같으나,
앞 32 바이트를 개인키라고 가정한 뒤 이를 이용해 공개키를 구하고,
부모 공개키와 점 덧셈을 구한 것이 자식 공개키이다.
(만일 앞 32바이트가 secp256k1에 정의된 n보다 크거나, 무한 원점이면 새로운 인덱스 사용해야)
텍스트로 보면 뭔소린지 하나도 모르겠다. 그림으로 보면 이해가 갈 것이다.
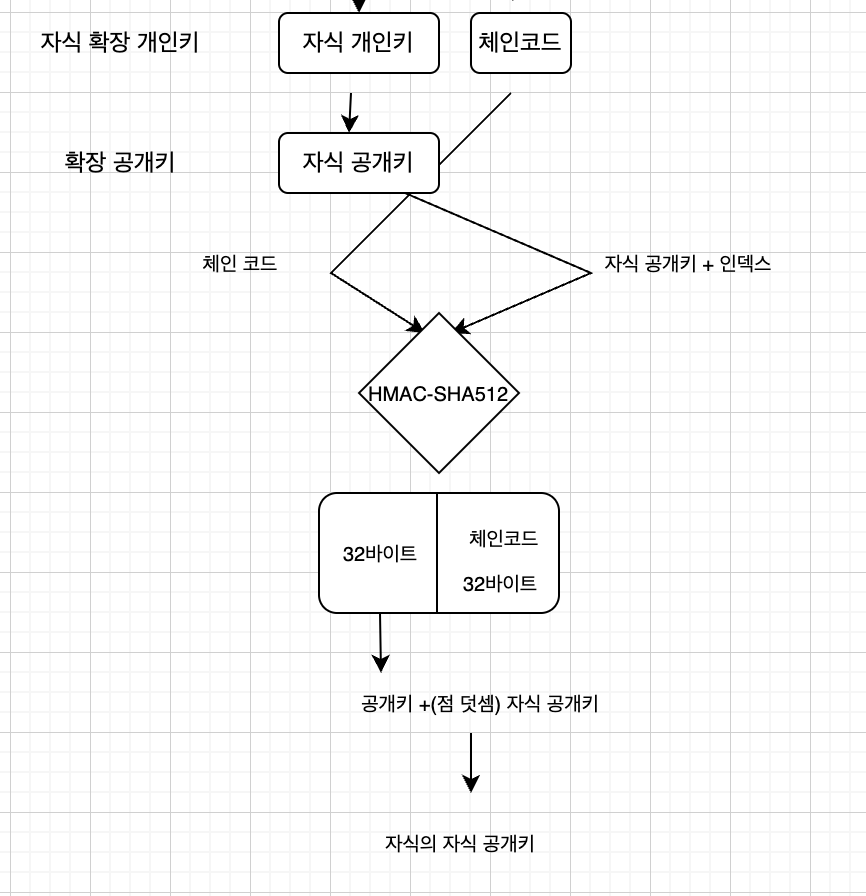
이상하다.
본래 개인키를 생성하고 공개키를 생성해야 되는데,
자식의 자식 개인키는 어디감? 공개키가 개인키에서 비롯되야지 뉴패턴 뭐임?
자식의 자식 개인키는
자식 개인키에서 일반 자식 키를 생성한 값이다.
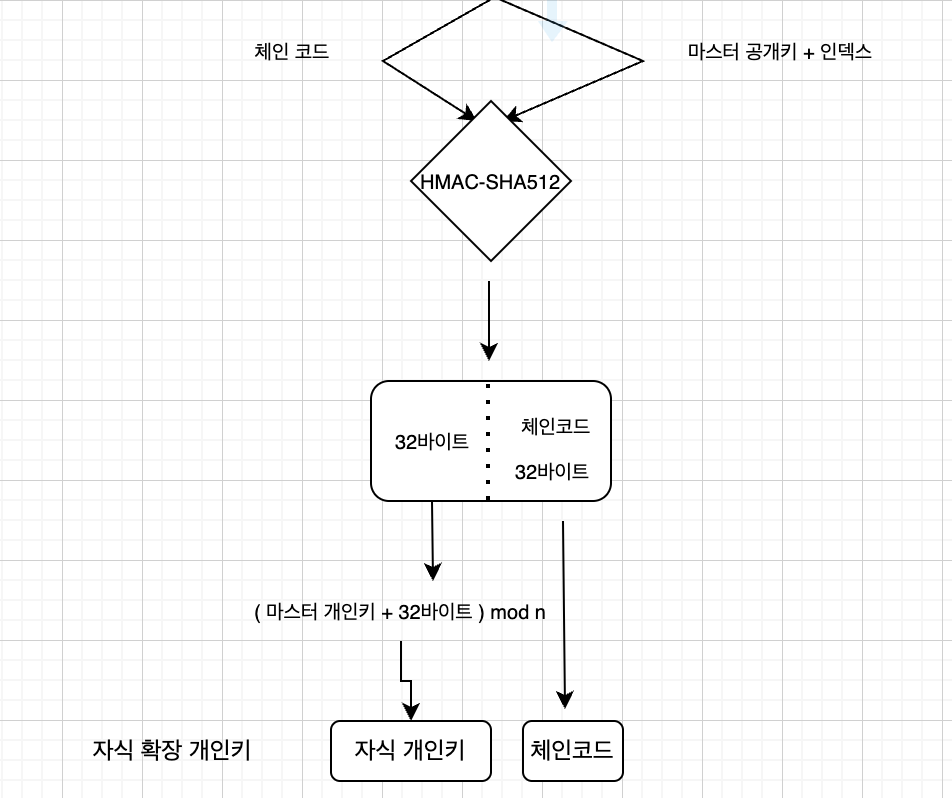
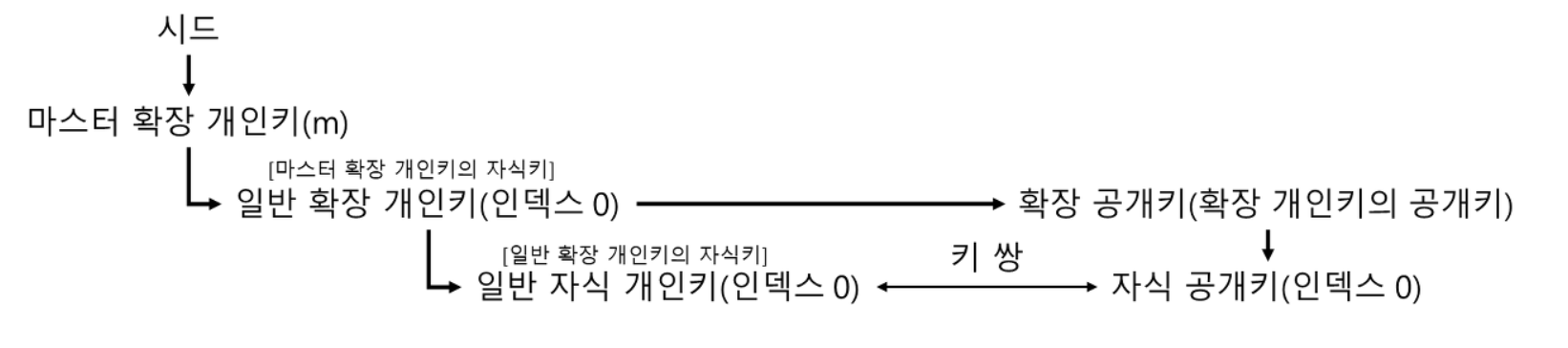
위 그림에서
마스터 공개키 => 자식 공개키
자식 개인키 => 자식의 자식 개인키
라고 상상하라 (그리기 귀찮다)
인덱스가 같다면,
- 확장 공개키를 이용한 공개키 만들기 => 공개키
- 일반 자식 키 만들기 => 개인키
가 쌍을 이룬다는 것이다.
2가지 방법을 사용했는데 둘이 쌍을 이룬다니!
부트캠프 강의에서
HD 월렛에서 시드와 인덱스만 알면 비밀키를 다 알 수 있다.
고 한 의미가 이거였구나.
2. BIP - 44
주제 : HD 지갑 파생 경로 표준 + 멀티 코인 지원
1. HD 지갑 파생 경로 표현 표준
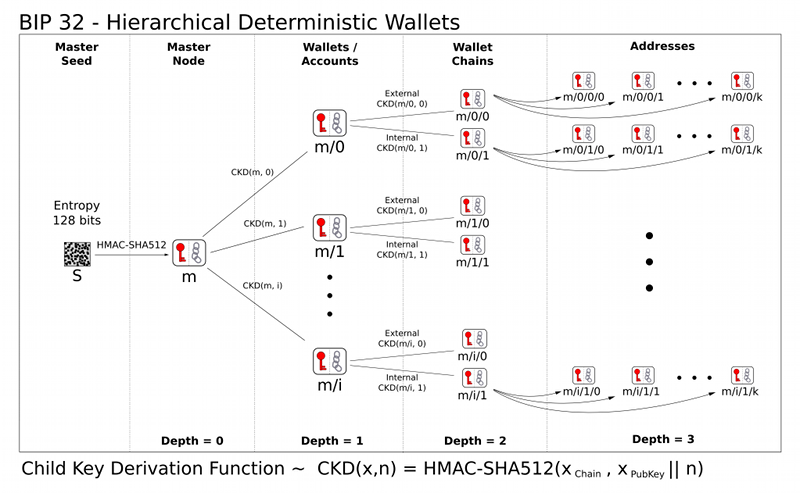
살짝만 위로 올라가서 저 그림을 보라. 토나온다.
매번 소통할 때 마다 그림으로 공유할래?
저걸 어떻게 간단하게 텍스트로 표준화할까? 에 대한 공식에 대한 제안이다.
마스터 개인키 = m
부모 개인키와 자식 개인키 관계는 '/'
자식 개인키의 인덱스를 정수로 적음.
강화 개인키인 경우 숫자 뒤에 ' 추가
정리하자면
m / 목적 ' / 코인 종류 ' / 계정 ' / 잔돈 계정 / 인덱스
순으로 표현한다.
- 목적 : BIP 번호, BIP-44라면 44' (강화 자식이면 ' / 아니면 그냥)
- 코인 종류 : 비트코인 0', 이더리움 60' (멀티 코인 지원을 위한)
- 계정 :
- 잔돈 계정 여부 : 비트코인은 UTXO를 사용하기에 잔돈 계정 필요 (잔돈 1 / 그 외 0)
- 인덱스 : 여러 개인키 파생을 위한 인덱스
자 문제
m/44'/0'/1/1/3 해석해라.
'BIP44 표준의 비트코인의 1번 계정의 3번째 잔돈 계정'
잔돈 계정 ? change
비트코인은 UTXO를 사용하기에, 잔돈 계정이 필요하다.
예를 들어 A의 지갑에는 총 100이 있고, 30을 B에게 보낸다고 쳐보자.
상식적으로 A는 100 => 70, B + 30 하면 될 거 같지만, 이건 이더리움의 상태이고,
비트코인의 경우 30을 B에 보내고, 나머지 70은 다시 나한테 보내야 한다.
그 때 잔돈을 받는 계정이 change 계정이다.
참고 문헌
https://kwjdnjs.tistory.com/84
https://kwjdnjs.tistory.com/85
https://arshbot.medium.com/hd-wallets-explained-from-high-level-to-nuts-and-bolts-9a41545f5b0
https://github.com/bitcoin/bips/blob/master/bip-0044.mediawiki
https://github.com/bitcoin/bips/blob/master/bip-0032.mediawiki
https://blog.naver.com/forkblock/221559838087
