본격적으로 Diffusion Paper 을 읽기전에
https://www.youtube.com/watch?v=uFoGaIVHfoE&t=4455s 를 보고
Diffusion 에 대해서 공부하였다

1 DDPM ( Denoising Diffusion Probabilistic Model )

Physical Intuition

• Diffusion 의 사전적 의미 - 확산 : 액체나 기체에 다른 물질이 섞이고, 그것이 조금 씩 번져가 마지막에는 일률적인 농도로 바뀌는 현상

• 연기의 밀도를 알아내는 것은 어려우나, 시간이 지나면 고르게 분포되어 uniform 해질것임 -> 딥러닝에서 uniform 에서 시작해서 다시 처음 상태로 되돌릴 수 있음

• 작은 sequence 에서의 확산은 forward와 reverse 모두 gaussaion 분포 안에서 다음 위치가 결정된다고 가정함

Denoising Diffusion Models

-> 이미지에 noise 를 더해서 gaussaian noise map을 만들고,
noise에서 reverse denoising process 를 거쳐서, 이미지를 생성하는 과정

noise 에서 이미지를 생성하는 과정을 training 하는 것을 Diffusion Model 이라함

Foward Diffusion Process (q)

• variance schedule $\beta _{t}$ 값을 이용하여 data에 약간의 noise를 추가하고 $x_{t}$ 가 $\sqrt[]{1- \beta _{t}}x_{t-1}$ 를 중심으로 하고 분산이 $\beta _{t}$ 인 정규 분포에서 샘플링됨

• 단계별로 점진적으로 진행되며 각 단계에서 노이즈의 양이 증가하여, 최종적으로는 데이터는 거의 노이즈만 남게 됨

• Foward Diffusion Process의 전체 과정은 모든 단계에서의 조건부 확률의 곱으로 표현되며, 각 단계는 독립적으로 진행되고, 이전 단계의 data noise 를 추가하여 다음 단계를 생성함
  

Diffusion Kernel

• t번의 sampling 을 통해 매 step 을 거쳐가면서 진행하지않고, $x_{0}$ 에서 $x_{t}$를 한번에 진행할 수도 있음
  
  
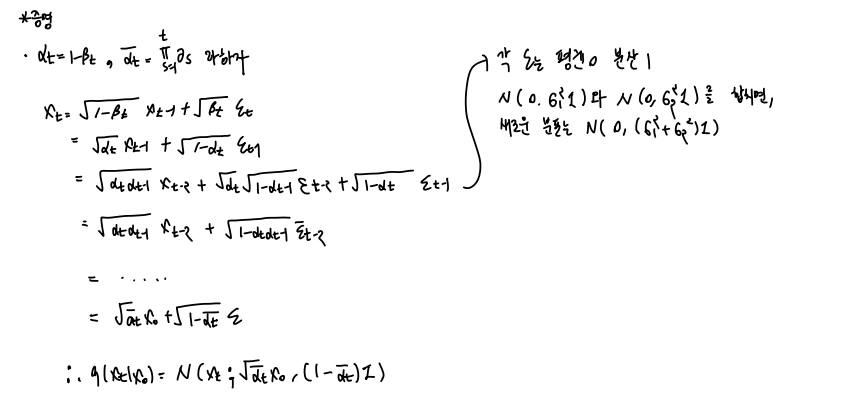
• $\alpha$ 를 이용하여 $x_{0}$에서 $x_{t}$를 만드는 과정을 한번에 sampling 할수 있음

Reverse Diffusion Process (p)

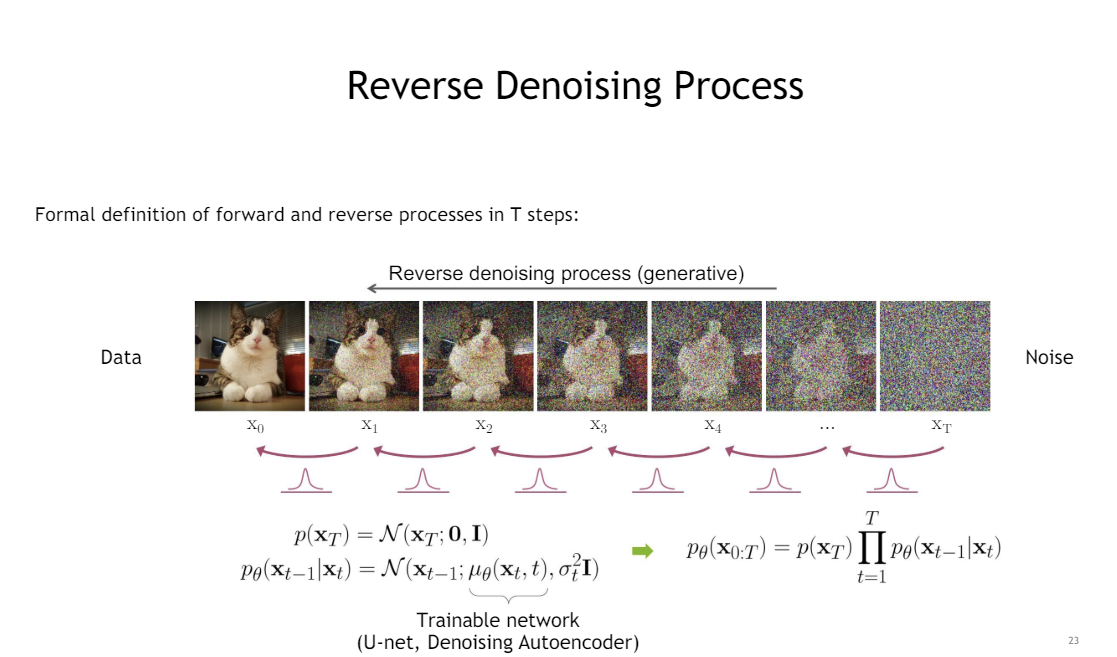
• 학습 가능한 네트워크 ( U-net, Denoising Autoencoder)로 평균된 학습과 고정된 분산을 이용하여 foward pass 를 수행한다

Learning Denoising Model ( Variational Upper Model )

Summary

Algorithm1 : Training
실제 데이터에 노이즈를 추가하여 노이즈가 포함된 데이터를 생성하고 , 모델이 예측한 노이즈와 실제 노이즈 간의 차이를 최소화 하는 파라미터를 업데이트함

Algorithm2 : Sampling
초기 노이즈 상태에서 시작하여, 모든 시간 단계에서 반복하면서,
현재 상태에서 예측된 노이즈를 제거하고, 모델의 불확실성과 다양한 샘플을 생성하기 위해서 노이즈를 추가하여 초기상태 xo을 반환함

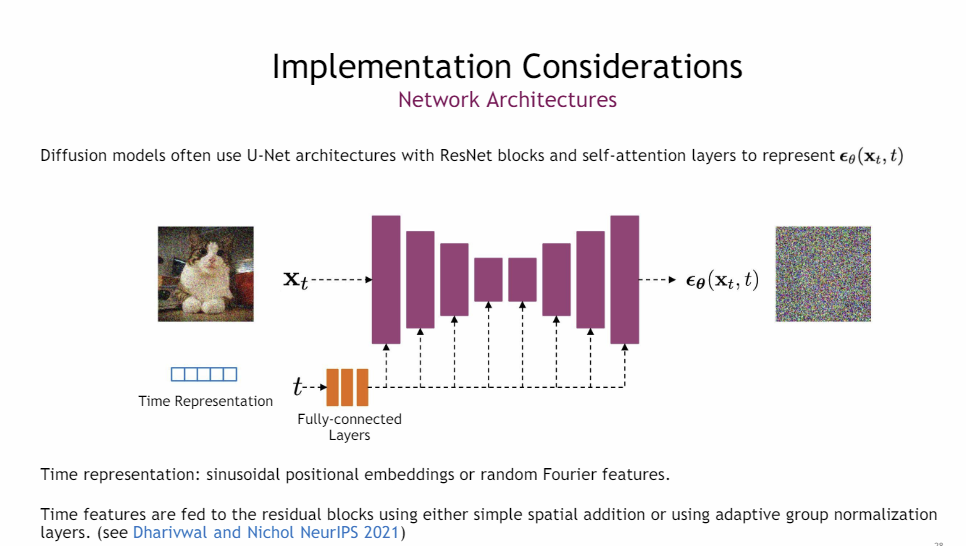
• 현재 시간 단계 t 에서의 $x_{t}$ 이미지와 현재 시간단계를 나타내는 값을 U-NET 구조에 넣어줌
• 출력값으로 시간 단계 t에 대해 예측된 노이즈를 출력하고 이를 사용하여 $x_{t-1}$ 를 생성함
• 최종적으로 $x_{0}$을 얻으며, 이는 노이즈가 제거된 원래 이미지임

2 DDIM ( Denoising diifusion implicit models )

DDPM 에서는 Markovian Process 라서 이미지 생성까지 많은 step 을 거쳐야하기 때문에 시간이 많이 걸려 non-Markovian Process 를 도입한 DDIM 을 제안함

• Markovian Process : 현재 상태가 바로 이전 상태에민 의존하며( $x_{t}$는 $x_{t-1}$로부터 결정 ) , 각 step 마다 현재 상태에서 다음 상태로의 전환이 이루어짐
• Non-Markovian Process : 현재 상태가 여러 이전의 상태의 영향을 미칠 수 있음( $x_{t}$와 $x_{0}$을 같이 이용해서 $x_{t-1}$을 결정 ) , 중간단계를 생략하고 여러 이전 상태들을 이용해 직접적으로 예측 가능

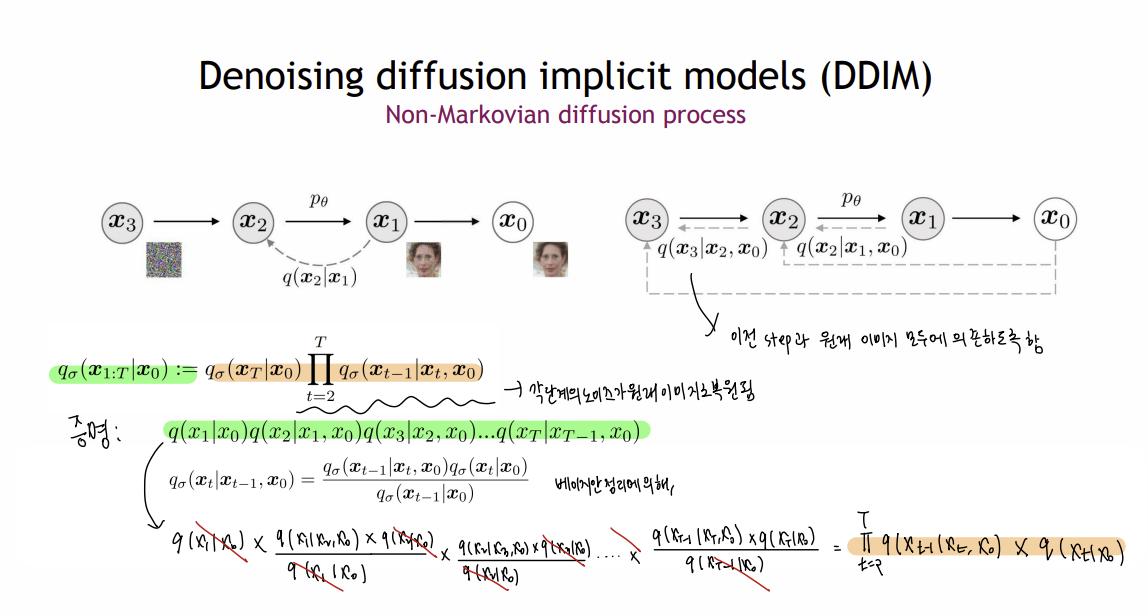
Non-Markovian Process 과정을 베이지안 정리에 따라서 정리한 과정이다

DDIM의 Reverse Diffusion Process 을 다음과 같으 표현할 수 있다

• sigma가 0이 되게 되면, random noise 성분이 제거되어, deterministic 된다. 이는 Reverse Diffusion Process에서 각 단계까 확률적으로 결정되지 않고, 특정한 값으로 고정됨

-> 즉, DDPM은 reverse duffusion process 과정에서 p라는 새로운 분포를 학습하여 실제 q에 근사하는 것이고 DDIM 은 원래 알고 있는 q를 직접적으로 사용함

3 Score-based Generative Modeling with Differential Equations

Forward Diffusion SDE

기존의 Foward Diffusion Process를 시간에 따라 noise 의 분포가 어떻게 변하는 지를 나타냄

• $\beta$(t)는 시간 t에 따라 노이즈의 크기를 조절하는 함수이며 식을 다음과 같이 정리할 수 있다
  (사진)

이산적인 시간 단계에서 연속적인 시간 단계로 변환된 확률 미분 방정식 (SDE)이다

Reverse Generative Diffusion SDE

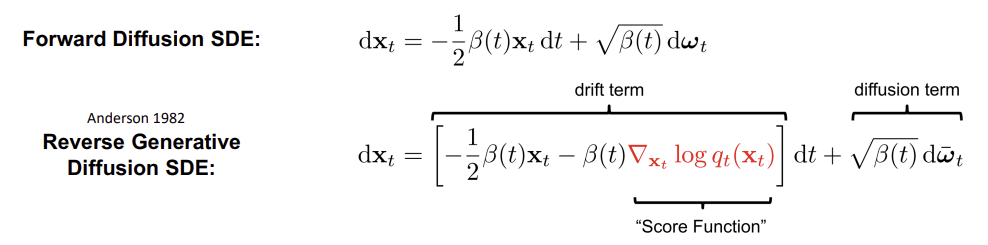
• Reverse Generative Diffusion SDE 에서 drift term 에 score function ( 확률밀도 함수 $q_{t}(x_{t})$ 의 로그 도함수로 데이터 분포의 변화율 ) 을 도입함

• 데이터가 밀집된 영역으로 모델의 수렴하도록 하여, 생성된 데이터가 원본 데이터와 더 유사하게 만듦

그러면 , $\bigtriangledown x_{t}log q_{t}(x_{t})$ 를 어떻게 구할 수 있을까?

Score Matching

score function 을 direct regression 방식으로 학습하는 모델에서는 $\bigtriangledown x_{t}log q_{t}(x_{t})$ 를 직접적으로 계산해야하는데, 이는 계산적으로 실현 불가능함

Denoising Score Matching

• $s_{\theta}(x_{t} , t)$ : 시간 t와 데이터 $x_{t}$를 입력으로 받아서 예측한 score function, $\theta$는 신경망의 parameter
• 주어진 초기 데이터 $x_{0}$로부터 확산된 $x_{t}$의 분포 $q_{t}(x_{t}|x_{0})$ 의 로그 확률밀도의 기울기를 계산할 수 있음
• 수식의 각 기댓값을 계산한 후 , 신경망 $s_{\theta}(x_{t} , t)$ 이 실제 score function $log q_{t}(x_{t})$ 에 근사하게 됨
  

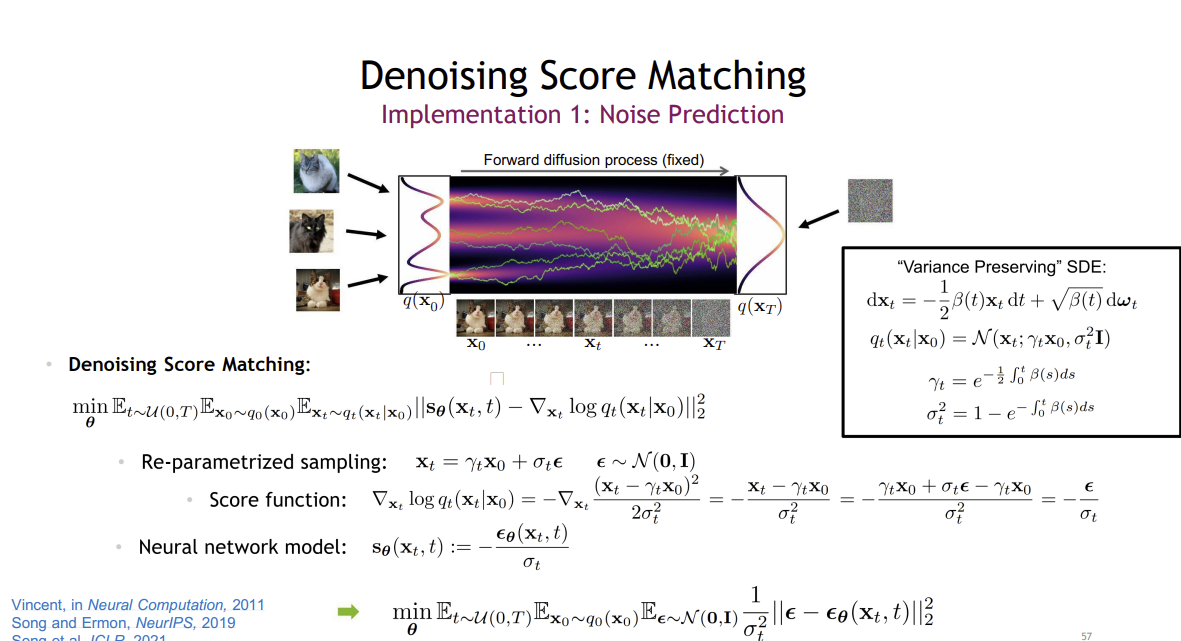
결론적으로 최종 최적화 과정을 다음과 같이 표현할 수 있다

$minθ​E_{t}∼U(0,T)​E_{x0}​∼q_{0}​(x_{0}​)​Eϵ∼N(0,I)​∥ϵ−ϵ_{θ}​(x_{t}​,t)∥​$
->DDPM과 DDIM의 Loss 함수와 매우 유사함을 확인 할 수 있음

Probability Flow ODE

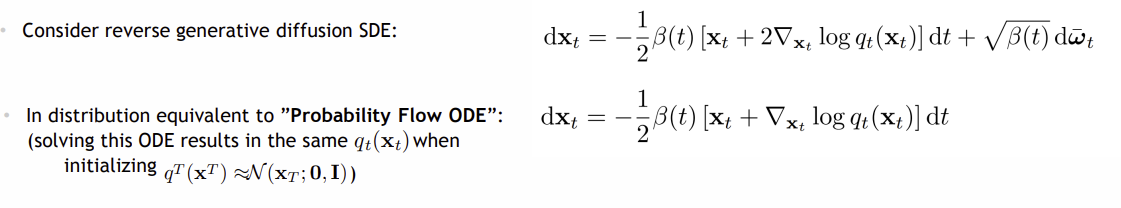
ODE 은 SDE 에서 noise 항이 없는 deterministic 로, 계산이 더 효율적이고 더 높은 안전성과 정확성을 제공할 수 있음

$f(x,t)=-\frac{1}{2}\beta(t)x_{t} , g(t)=\sqrt[]{\beta(t)x_{t}}$ 일때 다음과 같이 표현할 수 있으며,
Euler-Maruyama solver 방법을 활용하여 t=0이 될때까지 업데이트하여, SDE를 수치적으로 해결할 수 있음