1 Introduction

다양한 데이터에 대해서 높은 품질의 sample을 생성하는 Deep Generative Model 이 발전하였다. GAN , autogressive models, flows, VAE 등이 있으며, energy-based modeling 과 score matching 에서도 놀라운 발전이 있어, GAN과 비교할 만한 이미지를 생성해내고 있다.

본 논문은 Diffusion Probabilistc models 에 대해서 다룬다. Diffusion Probalistic models 은 데이터를 noise 로 변환하고 , 다시 noise를 제거하여 원래 데이터를 복원하는 과정을 통해 sample을 생성하는 모델이다. 이 과정은 Markov Chain (마르코프 체인) 을 기반으로 하며, Variational Inference (변분 추론) 을 사용하여 모델을 학습한다. 또한 각 단계의 전이는 조건부 Gauusian 을 사용하여 설정된다.

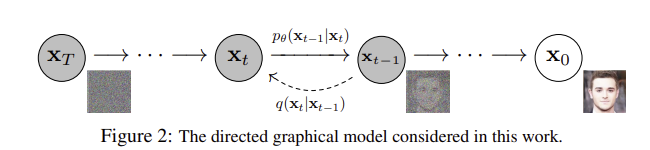
2 Background

Forward process

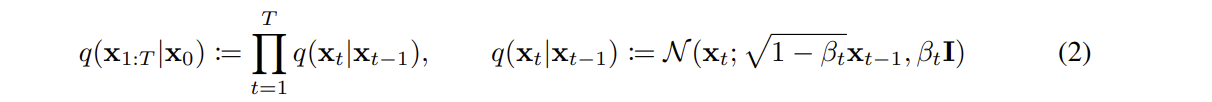
• q는 원래 데이터 $x_{0}$에서 시작되어 각 단계에서 Gaussian 노이즈를 추가하여 최종 상태의 $x_{T}$ 노이즈 이미지를 생성하는 과정이며, 최종적으로 매우 노이즈가 많은 $x_{T}$가 생성된다

• $q_{\theta }(x_{t}|x_{t-1})$ 로 forward pass를 표현할 수 있으며, 현재시점 $x_{t}$ 의 데이터 분포는 이전 시점 $x_{t-1}$ 에만 의존한다

• Diffusion Model 이 다른 latent vairable models와 다른점은 foward process, diffusion process 라고 불리는 approximate posterior $q_{\theta }(x_{1:T}|x_{0})$ 가 고정된 Markov Chain 으로, $\beta_{1}$ .... $\beta_{t}$ 에 따라 데이터에 점진적으로 Gaussian 잡음을 추가한다
  ( 고정된 Markov Chain이라고 하는 이유는, 사전에 정의된 $\beta_{1}$ .... $\beta_{t}$ 에 따라 고정되며, train 중에 변경되지 않기 때문)

• $q_{\theta }(x_{1:T}|x_{0})$ = $\prod_{T}^{t=1}q(x_{t}|x_{t-1})$에서

  1) $x_{1:T}$ 가 의미하는 것은 latent vector 들 $x_{1},x_{2},,,, x_{T}$ 를 나타내며,

  2) $q_{\theta }(x_{1:T}|x_{0})$는 $x_{0}$ 가 주어졌을 때, 각 단계에서 noise 가 추가된 $x_{1}$부터 $x_{T}$ 까지의 모든 latent vecotr들의 확률 분포

  3) $\prod_{T}^{t=1}q(x_{t}|x_{t-1})$ 는 각 단계의 조건부 확률을 곱한것으로 표현된다

  ---

  

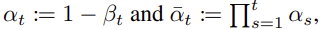
• $x_{0}$ 에서 $x_{T}$ 로 전개할 때, 0~T 의의 모든 수식을 step by step 으로 전개해야되기 때문에 많은 memory 를 소비하게 되고 시간도 오래걸리는 단점이 있음 이를 해결하기 위해 $\alpha$를 위와 같이 도입한다

• x 가 gaussaian Distribution을 따른다고 알려져 있을 때, reparameterization trick을 사용하여, 아래와 같이 나타낼 수 있음
  

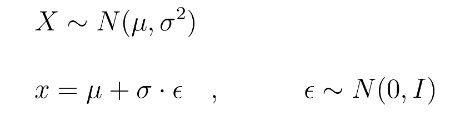
• $x_{t}$를 다음과 같이 표현할 수 있고,
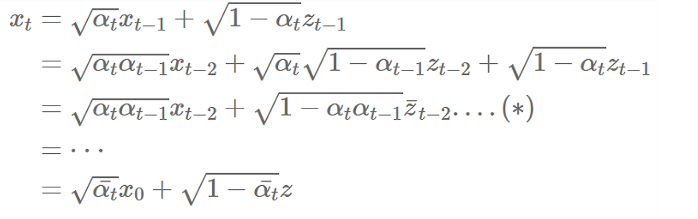  두개의 gaussian이 존재할때, 분산을 merge 하는 방법을 활용하여
  

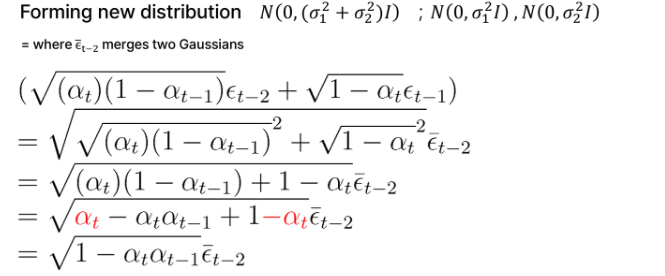
$q(x_{t}|x_{0})$ 의 평균과 분산을 결론적으로 다음과 같이 정리할 수 있다

---

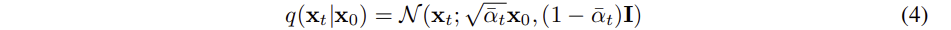
Reverse process

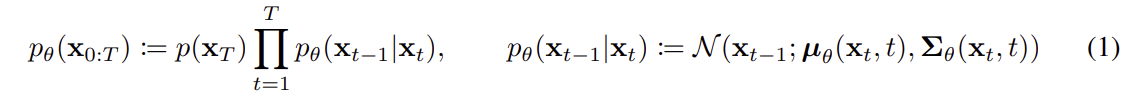
• random gaussian noise $x_{t}$ 에서 원본 이미지 $x_{0}$ 로 복구해 나가는 과정 inverse process $p_{\theta }(x_{t-1}|x_{t})$로 표현한다
• $p_{\theta }(x_{0:T})$ 는 $x_{0},x_{2},,,, x_{T}$ 의 연속적인 분포들의 joint distrubution 를 나타내며, 데이터 $x_{0}$ 를 생성하기 위한 전체 확률 과정을 의미 한다
• $p_{\theta }(x_{T})$는 $x_{T}$가 평균이 0이고 공분산이 단위행렬인 정규분포에서 sampling 된다
• $u_{\theta}(x_{t},t)$ 와 $\sum_{\theta} (x_{t},t)$ 는 train 과정에서 파라미터 $\theta$에 의해 결정되는 평균과 공분산 이다

---

Learning Denoising Model

$log p_{\theta}(x_{0})$ 를 최대화 하는것 즉 , $E[-log p_{\theta}(x_{0})]$를 최소화 하는 것이 목적이다

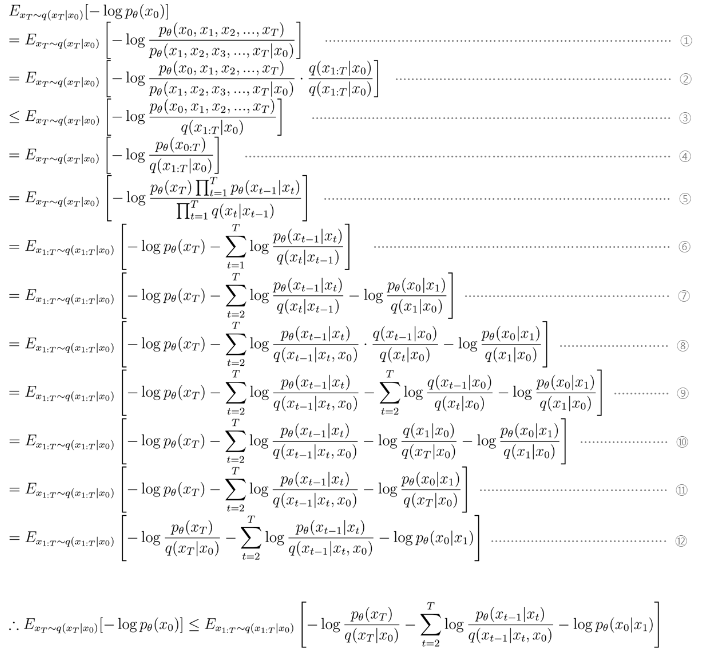
식을 정리하면 위와 같다

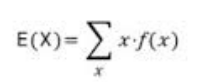
expectation 정리와, KL-divergence 를 활용하여 다시 정리해보면, 아래와 같다

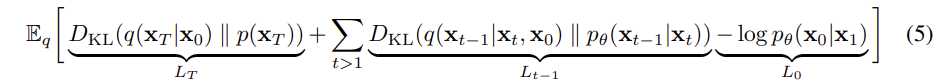
3 Diffusion models and denoising autoencoders

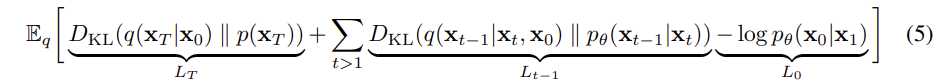
• $L_{T}$ : KL-divergence 를 통해, $x_{0}$에서 $x_{T}$를 생성하는 q분포와 p($x_{T}$) 분포가 유사해 지도록 함
• $L_{t-1}$ : diffusion process 와 reverse process 간의 분포가 유사해지도록 함
• $L_{0}$ : $x_{1}$ 에서 $x_{0}$가 나올 우도를 최대화 함

3.1 Forward process and $L_{t}$

foward process 의 분산 $\beta_{t}$가 reparameterization 을 통해 학습할 수 있지만, 이를 학습 가능하다고 생각하지 않고, 고정하여 상수로 취급한다. 따라서, approximate posterior q는 학습가능한 파라미터를 가지지 않으며, 그래서 $L_{T}$ 는 학습 중에 상수이므로 무시 될 수 있다

3.2 Reverse process and $L_{1:T −1}$

1. $L_{t-1}$에 분자항에 있는 $q(x_{t-1}|x_{t}, x_{0})$의 평균과 분산을 구하는 것이 필요하다

• 베이지안과, 가우시안 분포의 정규식, $q(x_{t}|x_{t-1}, x_{0})$, $q(x_{t-1}|x_{0})$, $q(x_{t}|x_{0})$의 평균과 분산을 활용하여 다음과 같이 나타낼 수 있음
  

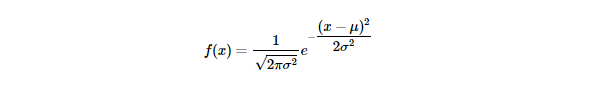
• 위에서 정리한 것을 토대로 평균과, 분산을 정리하면 아래와 같음
  

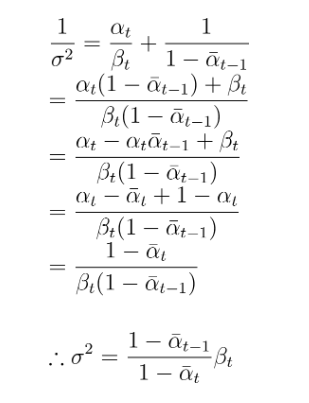
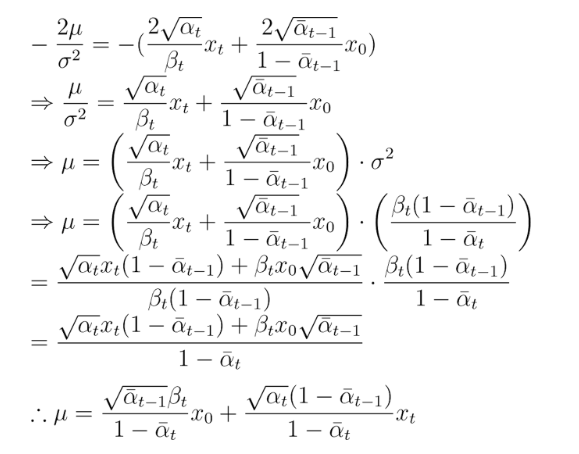
결론적으로 $q(x_{t-1}|x_{t}, x_{0})$의 평균과 분산은 다음과 같다

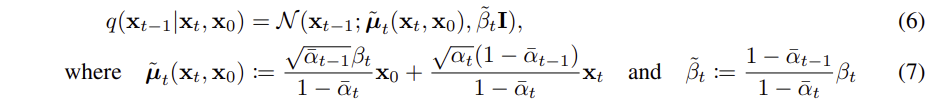
추가적으로, 정리를 해보자면

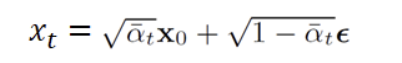
에 의해, $x_{0}$를 아래와 같이 변환 할 수 있어,

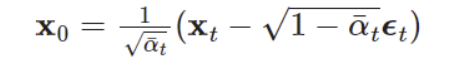
최종적으로 평균을 다음과 같이 정리할 수 있다.

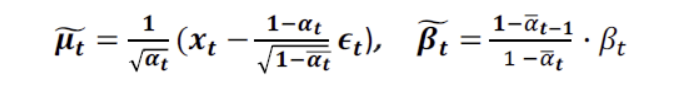
2. $L_{t-1}$에 분모항에 있는 $p_{\theta}(x_{t-1}|x_{t})$의 평균과 분산을 구하는 것이 필요하다

$L_{t-1}$ 를 minimize 하고자 하는 것이기 때문에, p의 분포를 q의 분포에 approximate 하는 것과 동일하다
q의 평균 식에서 $x_t$는 입력값이고, $\alpha$ 는 고정값이므로, 시간 t 에 따라 바뀔수 있도록 변화를 할 수 있는 부분(학습할 수 있는 parameter 는 ) 은 가우시안 분포 를 따르는 $\epsilon$ 이다

3.2.1 에서 구한 평균에서 $\epsilon$ 을 $\epsilon_t$ 로만 변경해주면 된다.

---

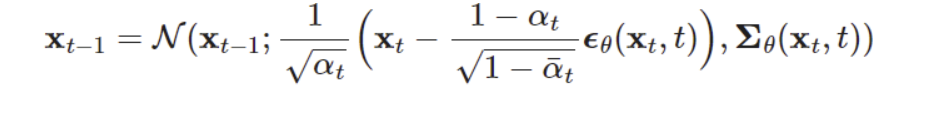
여기에서,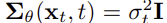
로 두어, timestep에만 의존하고 학습하지 않은 상수로 둔다

여기에서 $σ_t^2$ 를 둘중에 어떤 값으로 하든 유의미한 차이는 나타나지 않음

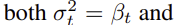
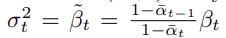
3. $L_{t-1}$ 을 간단히 해보면,

• p,q 두개의 분포가 가우시안 분포 일 때, KL-Divergence 식은 다음과 같이 표현이 가능하다
  ( 여기서 p= $N(u_{1}, \sigma_{1})$ , q= $N(u_{2}, \sigma_{2})$ )
  
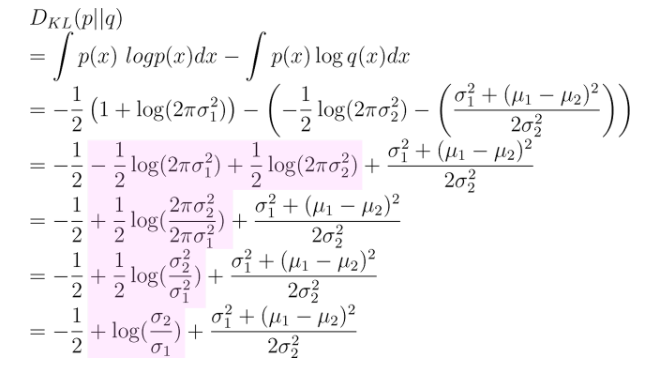
• $L_{t-1}$ 의 KL( q,p ) 에서 q, p 분산은 모두 학습 parameter 가 아니므로 $\sigma$ 를 상수처리 ( C ) 하면, $L_{t-1}$ 를 다음과 같이 표현이 가능하다
  

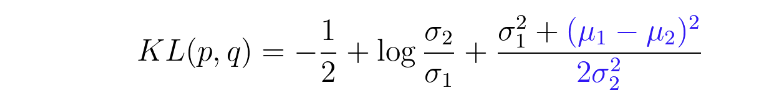
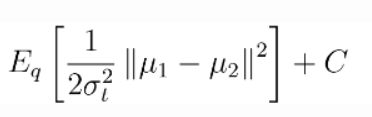
• $q(x_{t-1}|x_{t},x_{0})$ 의 평균과 $p_{\theta}(x_{t-1}|x_{t})$ 의 평균을 이용하여. 최종적으로 다음과 같이 표현할 수 있다
  

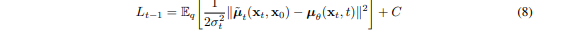
4. 최종적으로 DDPM Loss 계산

• 3.2.1 과 3.2.2 에서 정리한 $q(x_{t-1}|x_{t},x_{0})$ 의 평균 $\tilde {\mu} _t (x_t, x_0)$ 과
  $p_{\theta}(x_{t-1}|x_{t})$ 의 평균 ${\mu} _{\theta} (x_t, t)$ 은 아래와 같다
  
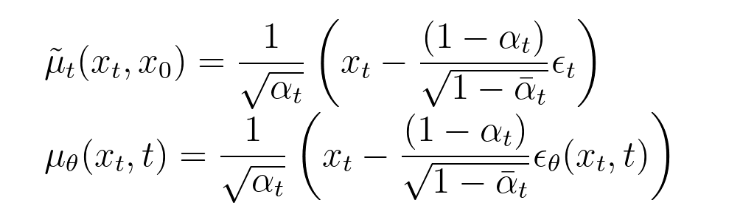
• 3.2.3 에서 정리한 $L_{t-1}$ 에 대입하여 식을 정리한다
  
  최종적으로 DDPM 의 loss function을 다음과 같이 정리할 수 있다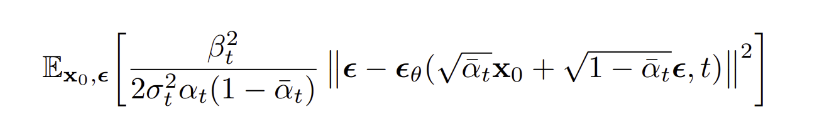

3.3 Data scaling, reverse process decoder, and $L_{0}$

이미지 데이터를 [-1, 1] 범위로 scaling 한다. 이는 모든 reverse process 가 항상 scaling 된 input 으로 진행된다는 것을 보장한다. 이산적인 log-likelihodd 를 얻기 위해, reverse process의 가장 마지막과정 ( $x_1$ 으로 부터 $x_0$ sampling 하는 과정) 은 정규분포$N(x_0​;μ_θ​(x_1​,1),σ_1^2​I)$ 를 사용하는, 이전과 독립적인 discrete decoder 를 가진다

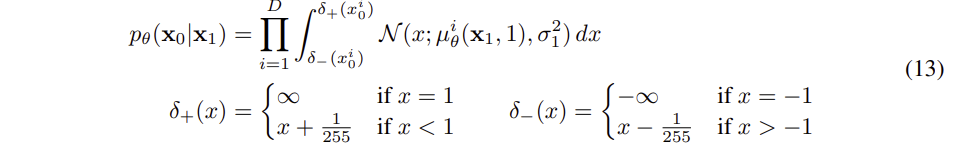
3.4 Simplified training objective

실제 train 할 때는, 앞에 곱해져 있는 weight term을 제거하는 것이 성능이 잘나와서, 뒷 부분만 사용하여 loss 를 계산한다

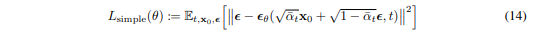
• Training 과정에서 $\epsilon_{\theta}$ 를 학습하여 , 수렴할 때까지 반복한다

• Sampling 과정에서 훈련된 모델을 사용해, 데이터 분포의 sample을 생성하여 최종적으로 $x_0$ 을 생성한다

---

<참고>
https://xoft.tistory.com/33
https://woongchan789.tistory.com/12