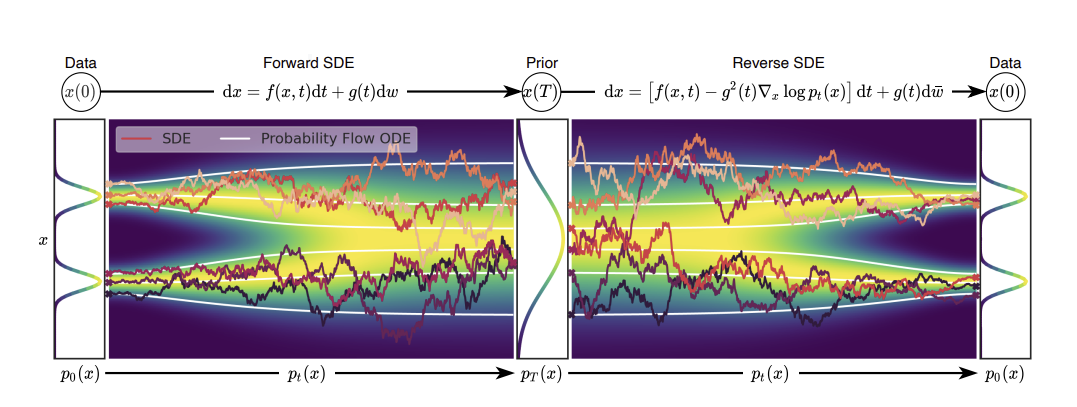
1 Introduction

probabilistic generative model 중에서 대표적으로 SMLD (Score Matching with Langevin Dynamics) 와 DDPM (Denoising Diffusion Probabilistic Modeling) 가 있다.

SMLD는 다른 sclae 의 noise 를 점차적으로 추가하여 변형시켜 데이터의 확률분포를 학습하고, Langevin Dynamics 를 통해 probability gradient ( score ) 따라가면서 점진적으로 sampling 한다.

DDPM은 연속적인 시간에 따라 noise를 점진적으로 추가하며 reverse process에서는 noise를 제거하는 probaility model을 학습하여 model을 점진적으로 복원하여 samling 한다.

이 논문에서는 기존 방식의 한정된 ( 이산적인 ) 수의 noise 분포를 사용하는 대신, 시간에 따라 연속적으로 변확하는 확률 분포를 사용하는 SDE 방식을 제안한다.

forward process와 reverse process 모두 SDE로 설명할 수 있으며, reverse process 과정에서는 Score of the probability density over time (gradient of the log probability density)를 학습하여 noise 를 제거하는 방법을 학습하게 된다.

2 BackGround

2.1 Denoising Score Matching With Langvin Dynamics ( SMLD )

Noise Conditional Score Networks ( NCSN ) 를 train 하는 방법에 대한 설명이다.

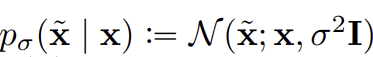
• 평균이 x이고 분산이 $\sigma^2$ 인 가우시안 분포에서 $\tilde{x}$를 sampling 한다. 즉 원본 데이터 x에서 평균이 0이고 분산이 $\sigma^2$인 random noise 를 추가해 $\tilde{x}$ 를 만든다.

• noise scale $\sigma_1 < \sigma_2 < \cdots < \sigma_N$ 은 점점 커지게 된다.
  
  

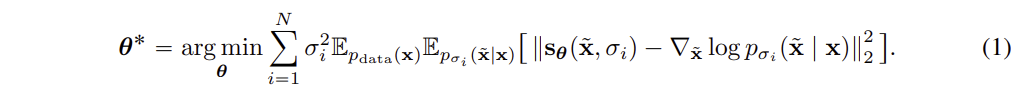
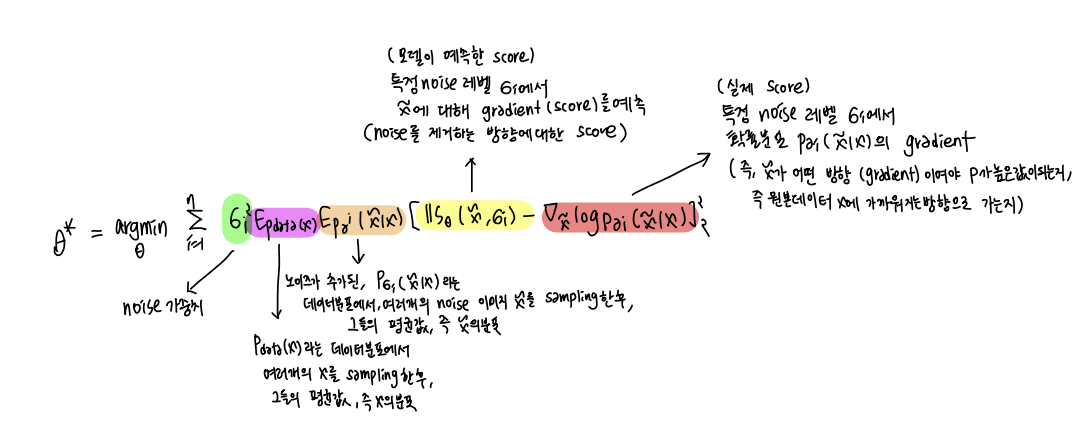
• 손실함수는 위와 같다. 실제 score와 예측한 score를 최소화하는 방향으로 학습한다. 여기서 예측 모델은 noise 가 섞인 데이터가 원본데이터 x를 복원하는 방향으로 score
  ($\tilde{x}$ 가 어떤 gradient (방향) 으로 움직여야 x 가 될 확률이 높은지) 를 예측하는 모델이다.

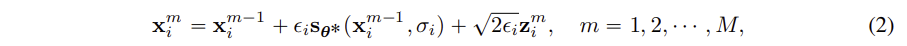
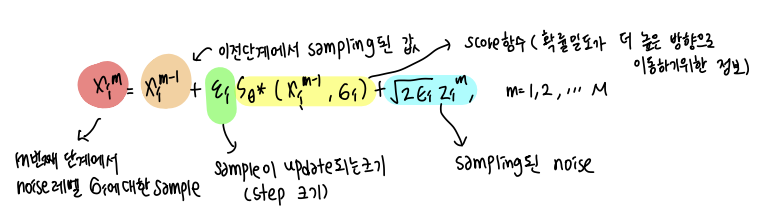
• Langvin MCMC 는 확률적 sampling 방법으로, score 함수를 사용해 확률 분포로부터 sample 을 생성하는 방법이다. 위와 같이 M 단계에 걸쳐 점차적으로 sample 을 얻으면서 최종 sample을 얻는다.
• 큰 noise 수준에서 점차적으로 작은 noise 수준으로 이동하며, 확률 분포의 socre 에 따라 sample을 점진적으로 업데이트한다. 한 noise 에서 M단계를 걸쳐 sampling 이 진행되면, 그 다음 noise 수준으로 이동해서 반복한다. M 이 충분히 크고 step 크기가 작아지면, 원본 데이터에 가깝게 복원이 된다.

2.2 Denoising Diffusion Probabilistic Models( DDPM )

Forward Process ( Diffusion Process )

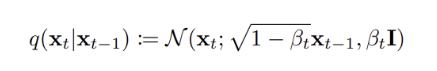
• Foward Process : 특정 단계 $x_t$가 $x_{t-1}$ 에 의존하여 어떻게 분포하는지 의미하며, 이 과정은 Gaussain 분포를 따른다. 여기서 $\beta$는 noise 의 크기를 의미한다.

  ---

  

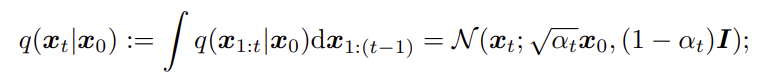
• Markov Chain을 통해, moise 가 추가된 데이터 $x_t$ 가 원본 데이터 $x_0$ 로 부터 생성되는 데이터 분포를 의미한다. $\alpha_i = \prod_{j=1}^{i} (1 -\beta_j)$ 는 여러 단계에 걸쳐 노이즈가 누적된 정도를 나타낸다.

Reverse Process

• noise 가 추가된 데이터 $x_i$를 기반으로 이전상태 $x_{i-1}$를 예측한다.
• 식은 $p_\theta(x_{i-1} | x_i) = N(x_{i-1}; \sqrt{1 - \beta_i} x_i + \beta_i s_\theta(x_i, i), \beta_i I)$
  와 같이 정의할 수 있다. 여기서 s는 score model 로 원본 데이터 $x_0$ 를 향한 방향 ( gradient ) 를 예측하는 역할을 한다.

ELBO ( 손실함수 )

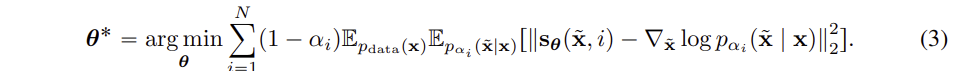
• loss 함수는 예측하는 score 가 실제 score와 얼마나 가까운지를 예측하면서 파라미터가 업데이트되면서 학습된다. 즉, noise 가 추가된 데이터를 원본 데이터로 복원하는 과정을 얼마나 정화하게 예측할 수 있는지를 평가한다.

Sampling

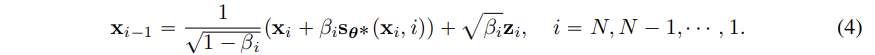
• sampling은 평균이 0 이고 분산이 1인 가우시안 분포로 부터 시작하여, 학습된 score 함수를 활용하여, estimated reverse Markov chain 을 사용하여 noise 를 점진적으로 제거하여 원본 데이터에 가까운 sample을 생성한다.
• reverse Markov chain은 위와 같고, 각 단계에서 score 함수를 사용하여, noise 를 제거한다. 각 단계에서 random nosie ( $\beta_i z_i$) 를 추가하지만, $\beta$ 가 점차 줄어들면서 noise 도 점차 감소한다.

3 Score-Based Generative Modeling with SDES

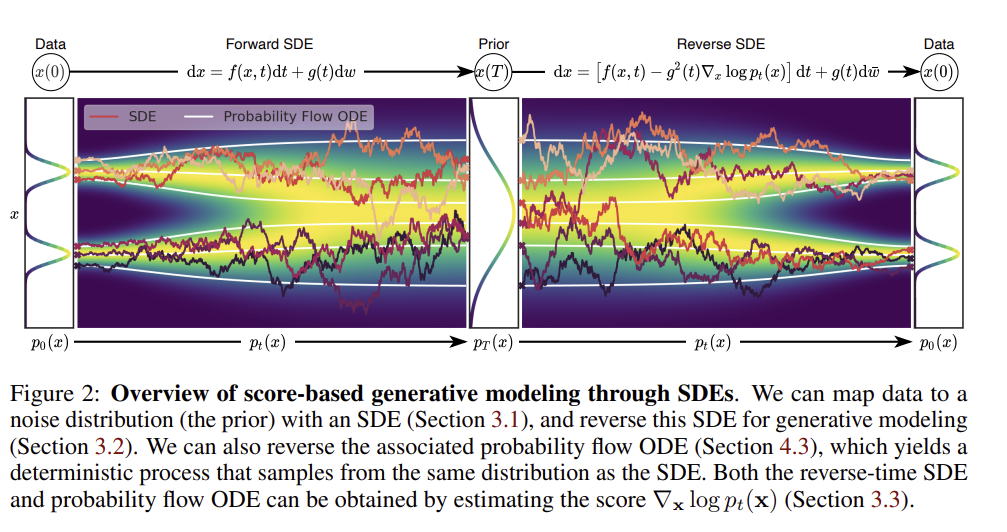
여러 단계의 noise scale로 데이터를 변형(복원) 하는 것이 이전 방법들의 성공에서 중요한 역할을 했다. 그렇기 떄문에, noise sclae 을 infinite number로 ( 무한한 개수 ) 로 확장하는 바업ㅂ을 제안하고 있다. noise 가 증가함에 따라 변형된 data 분포가 SDE 에 따라 변화게 된다.

3.1 Perturbing Data With SDEs ( Forward Process)

본 논문의 목표는 $x(0)$ ~ $p_0$ 가 데이터의 분포이고 $x(T)$ ~ $p_t$ 사전확률분포가 되도록 연속시간변수 $t \in [0, T]$ 에 의해 표현되는 diffusion process $\{x(t)\}_{t=0}^T$ 를 만드는 것이다.

용어정리
x(0) : noise 가 추가 안된 image
x(t) : t 시점에서의 noise 가 추가된 image
$p_t(x)$ : 시간 t에서의 데이터 x의 확률밀도함수, 즉 t에서 데이터 x 가 어떤 값을 가질 확률을 의미 , 픽셀이 해당 특징을 가질 확률 분포를 의미함

Diffusion 과정을 설명하기 위해 SDE 를 사용한다.

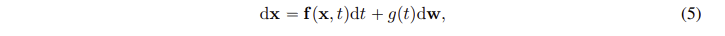
시간에 따른 데이터의 변화를 위와같이 표현할 수 있다.

$f(x,t)$ 는 drift coefficient로 시간 t에 따라 데이터가 어떻게 변하는지 나타낸는 방향을 의미하고 dt( 아주작은 변화량 ) 을 곱해주어, 아주 작은 시간 t에 따른 변화량을 의미한다.

$g(t)dw$는 diffusion coeffficent 로 시간 t에 따른 random noise의 크기를 의미한다.
여기서 w는 Winer process 로, 시간에 따라 무작위로 변화는 요소이다.

SDE에서 f나 g가 급변하지 않는다면, 즉 립시츠 조건 (Lipschitz Condition) 조건을 만족한다면, 유일한 해를 가진다.

3.2 Generating Samples by Reversing the SDE ( Reverse Process )

$p_t$에서 $p_0$ 방향으로 reverse process sampling 을 진행한다.
reverse process 과정을 diffusion process 의 reverse로 진행할 수 있으며 reverse-time SDE을 따른다.

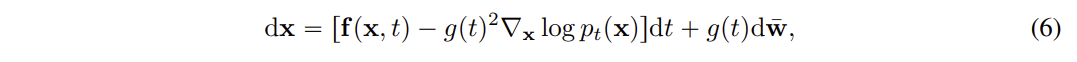
score 함수 $\nabla_x \log p_t(x)$ 를 활용하에 데이터가 어떻게 원본 상태로 복원될 수 있는지, 즉 확률 밀도의 기울기인 socre 함수를 사용하여 어떻게 하면 원본 상태에 가까워질지 알려준다.

3.3 Estimating Scores for the SDE

denoising score matching 을 사용하여, 시간에 따라 변화하는 데이터 본포의 gradient 를 예측하는 모델을 최적화하는 방법을 설명한다.

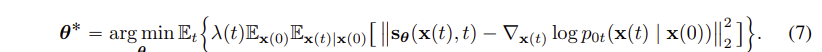
$s_\theta(x(t), t)$는 시간 t에 따른 데이터 x(t) 에 대한 gradient, 즉 score-based 모델이 예측한 값이다. noise 가 섞인 데이터 x(t)를 보고 noise 를 제거하는 방향 gradient 를 예측하는 모델이다.

$\nabla_{x(t)} \log p_0^t(x(t) | x(0))$는 실제 gradient 값으로, x(0) 에서 시작한 데이터가 시간이 지나면서 t 시점에 도달했을 때 x(t)에 있을 확률을 나타낸다.

3.4 Exapmles : VE, VP SDEs and Beyond

Score based Genertative Model 인 SMLD 와 DDPM 을 SDE 관점에서 설명한다.

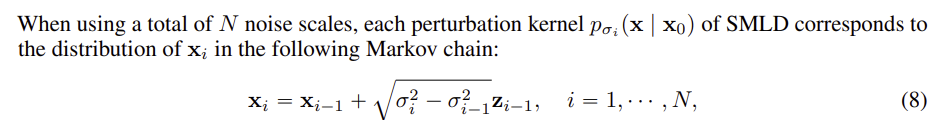
위의 식은 SMLD 에서 noise 과정이 어떻게 Markov chain으로 표현될 수 있는지 보여준다.

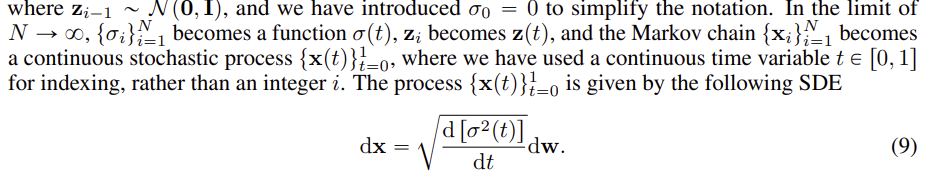
SMLD 에서 이산적인 noise 과정은 시간이 연속적인 경우 SDE로 변환될 수 있으며 그 식은 위와 같다. 위 방적은 Variance Exploding (VE) SDE로 불리면, 시간이 무한대로 갈 때 분산이 explode 하게 된다.

---

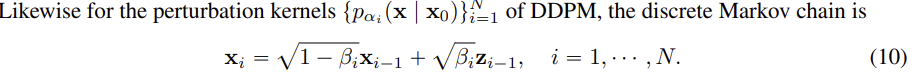
위 식은 DDPM 에서 사용하는 noise 과정이 Markov chain 으로 표현될 수 있는지 보여준다.

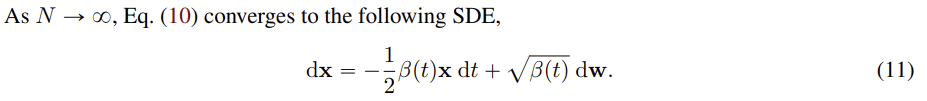
위에서와 마찬가지로, 연속적인 확률 과정이 된다면 (VP) SDE로 나타낼 수 있다. 이 식은 시간이 지나도 분산이 고정된 상태로 유지되는 특징이 있다.

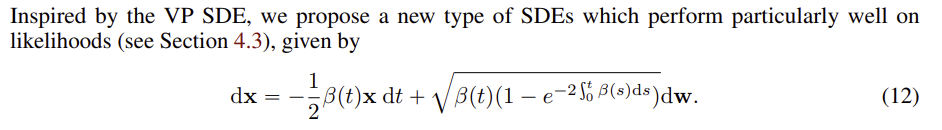
이 논문에서 VP SDE 에서 영감을 얻어서 새로운 SDE 를 제안한다. 새로 제안한 SDE 는 sub-vp SDE 라고 부르며 noise 추가 항을 확장하였다. sub-VP SDE 에서는 시간이 지남에 따라 점진적으로 noise 의 강도를 증가시킨다.

4 Solving the Reverse SDE

4.1 General Purpose Numerical SDE Solvers

SDE에서 numerical solvers를 활용하여 근사한다. SDE 같은 복잡한 방정식은 풀기 어렵기 때문이다. Euler-Maruyama와 Runge-Kutta와 같은 방식이 있다. 이 방법들은 Reverse SDE에도 적용되어, 데이터를 sampling 할 수 있다.

DDPM 에서 새로운 SDE를 적용했을 때 Ancestral Sampling 방식을 유도하는 것은 매우 어렵기 때문에 Reverse Diffusion Samplers 방법을 제안한다.

Reverse Diffusion Samplers는 forward process 에서 사용한 방식과 동일한 방법으로 reverse process 를 수행하는 과정을 말한다.

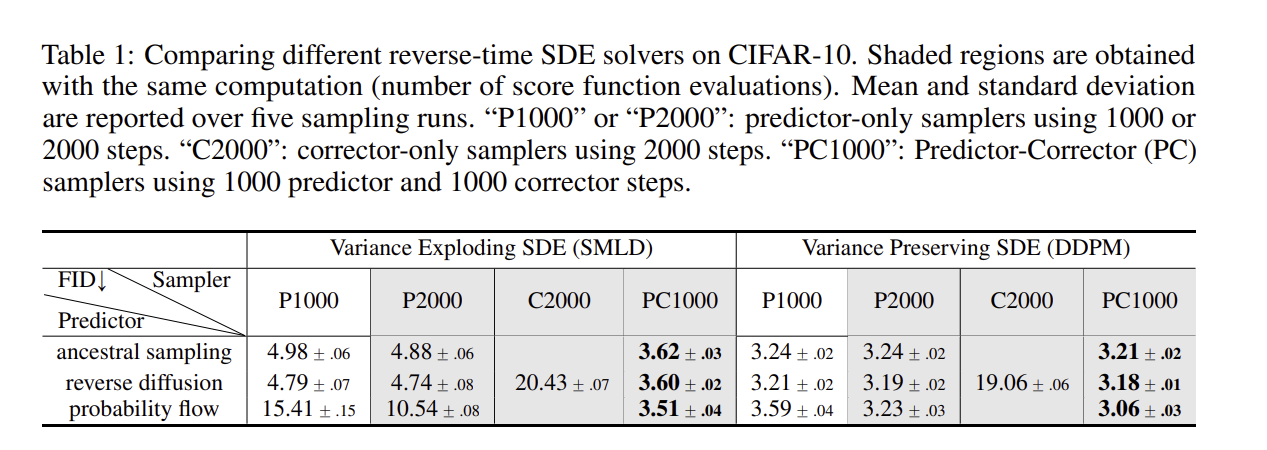
Reverse Diffusion Samplers 는 SMLD 와 DDPM 에서 Ancestral Sampling 보다 더 나은 성능을 보인것을 아래의 표를 통해 확인할 수 있다.

4.2 Predictor-Corrector Samplers

Predictor-Corrector (PC) sampler 를 도입한다. Predictor는 다음 단계에서 데이터가 어떻게 변할지 예측한다.

Corrector는 score 기반 model을 사용해서 예측값을 더 정확하게 수정한다.

SMLD나 DDPM의 기존 방식은 predict이나 correct 하나만 사용하지만 PC sampler는 predict 와 correct 를 모두 사용하기 때문에 samoling 이 더 정확해진다.

4.3 Probability Flow and Connefction Neural ODEs

Score Based Model 은 Reverse SDE 를 수행하기 위해 다른 방법을 제시한다. Diffusion process 에는 deterministic 하게 가능하다. SDE에서 파생된 ODE 로 표현할 수 있다.

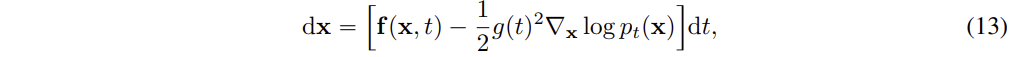
위 식은 Probability Flow ODE 라고 불리며, score 함수가 시간에 따라 변화하는 모델을 ( Neural ) 을 통해 근사하게 되면 위 과정은 Neural ODE의 예시가 된다.

Exact Likelihood Computation

Neural ODE를 사용하면 Probability Flow ODE를 통해 데이터를 시간에 따라 변화시키면서, 해당 데이터가 특정 분포에서 나올 확률(likehodd) 을 정확하게 계산할 수 있다.

Manipulating latent representations

Probability Flow ODE를 사용하면 데이터를 latent space로 인코딩할 수 있다.
데이터를 다시 디코딩할 때는, 역방향 SDE에 해당하는 ODE를 적분하면 된다.

Uniquely identifiable encoding

대부분의 모델에서는 인코딩된 정보가 완전히 고유하지 않을 수 있지만, 이 모델은 데이터 분포에 의해 고유하게 인코딩된다. 즉, 충분한 데이터와 좋은 모델을 사용하면, 각각의 데이터는 고유한 방식으로 인코딩된다.

Efficient sampling

Neural ODE 처럼 Probability Flow ODE 를 사용하여 data를 sampling 할 수 있다. Black-box ODE solver 라는 일반적인 ODE solver 를 사용하면 , 계산량을 90% 이상 줄이면서 높은 품질을 sample 할 수 있다.