[Paper Review] Diffusion Models Beat GANs on Image Synthesis

황영서·2024년 7월 30일

Diffusion

목록 보기

4/6

1 Introduction

GAN은 image generation에서 높은 성능을 보여주고 있지만, mode collapse 문제가 있고, 적절한 hyperparmaeter와 regularzation 기법이 없으면 train이 불안정하고, 새로운 domain에 적용이 어려울 수 있다.

GAN과 유사한 sample 품질을 달성하기 위해 likelihood-based 모델이 연구되었고, 이 모델들은 더 다양하게 sampling하고 train이 쉽고, 새로운 domain에 적용이 가능하지만, sampling 한 이미지의 품질이 좋지않고, VAE를 제외하면 sampling속도가 GAN에 비해 느리다.

Diffusion model은 likelihood-based 모델이며, 고품질의 이미지를 생성하는 것으로 알려져 있으며, distribution coverage를 잘 제공하고, training objective가 고정되어있고, 확장성이 쉽다. Diffusion model은 점차적으로 노이즈를 제거해가면서 이미지를 sampling하고, 그리고 traning objective는 variational lower-bound로 표현된다. Diffusion model은 CIFAR-10에서 좋은 성능을 보이지만, LSUN과 ImageNet과 같은 데이터셋에서는 여전히 GAN보다 뒤쳐진다.

Diffuson model과 GAN의 차이가 나는 이유가 GAN은 아키텍처가 많이 개선되었고, diversity를 희생하고 품질을 높였기 때문이다. Diffusion에서는 GAN에 이러한 이점을 활용하고자하는게 이 논문의 목표이다.

2 BackGround

DDPM에 대해서 다시 정리한다

Diffusion model은 noise를 추가하는 과정을 역으로 진행하여 sampling을 진행한다. noise $x_T$ 에서 시작하여, 점진적으로 noise 가 줄어든 sample $x_{T-1}$ , $x_{T-2}$ 를 생성하여 최종 sample $x_{0}$ 에 도달한다. $x_t$ 는 $x_0$ 와 노이즈 $\epsilon$ 으로 표현이 가능하다.
Diffusion model 은 $x_t$ 에서 $x_{t-1}$ 로 갈 수 있도록 학습한다. $x_t$ 의 노이즈 성분 $\epsilon_{\theta}(x_t, t)$ 를 예측한다. 학습 목표는 실제 노이즈와 예측된 노이즈 간의 MSE, 즉 $\|\epsilon_{\theta}(x_t, t) - \epsilon\|^2$ 를 최소화 하는것이다.
reverse process를 다음과 같이 표현할 수 있고,
,
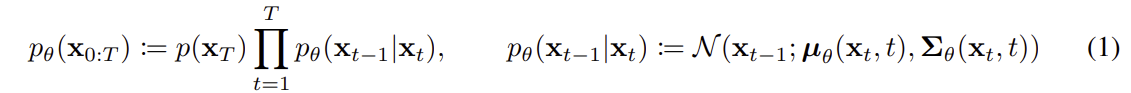평균은 $\epsilon_{\theta}(x_t, t)$ 를 활용하여, 다음과 같이 나타낼 수 있다.

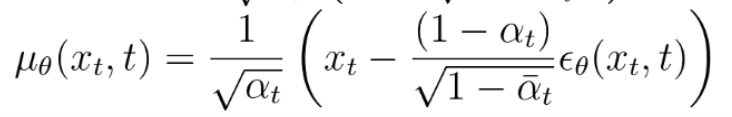분산은 상수로 고정한다

$L_{simple}$ 가 실제 variational lower bound 보다 더 잘 작동하는 것을 확인할 수 있었다.

2.1 Improvements

DDPM 에서는 $\Sigma_{\theta}(x_t, t)$ 를 상수로 고정했지만, DDIM 방식으로 sampling 하게 되면, 상수로 고정하면 최적의 방식이 아니기 때문에, $\Sigma_{\theta}(x_t, t)$ 를 다음과 같은 식으로 표현한다.

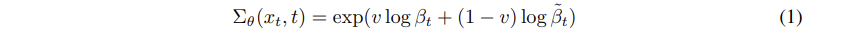
여기서 v는 모델이 학습을 통해 얻는 예측된 값이다. $\beta$ 와 $\tilde{\beta}$ 는 reverse process 에서의 분산의 상한과 하한을 의미한다.

또한 다음과 같이 hybrid loss 를 사용함으로써, sampling 단계를 줄이면서도 sampling 품질이 저하되는것을 최소화 할 수 있다.

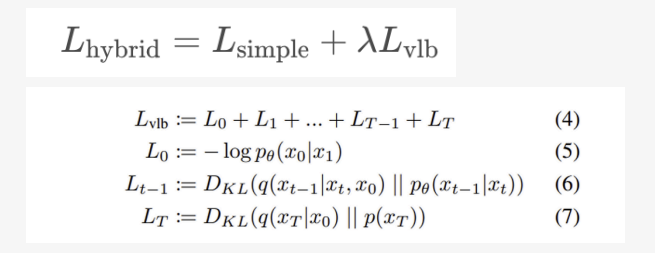
2.2 Sample Quality Metrics

서로 다른 모델이 생성한 sample의 quality를 비교하기 위해 다음 metric을 사용한다.

Inception Score ( IS ) : 모델이 데이터셋의 각 class 에 대해 상성한 sample의 집합이, 전체 class distribution을 얼마나 잘 나타내는지
FID score : IS 보다 인간의 평가와 더 유사한 결과를 나타내는 척도로 알려져 있다.
Precsion , Recall
Precision : sampling 한 것 중에 data manifold 에 존재하는 비율을 측정
Recall : sampling 한 것 중에 manifold에 속하는 data point의 비율

-> 논문에서 diversity와 sample의 품질을 동시에 측정하기 위해서 FID score를 기본 metric으로 사용하고 quality 측정을 위해 precision과 IS를 diversity를 측정하기 위해 recall을 사용한다.

3 Architecture Improvements

Diffusion model 구현을 위해 U-Net 아키텍처를 도입하였다.
U-Net 은

downsmpling과 upsampling과정으로 이루어져있고, residual connection을 통해 Decoder에 Encoder의 정보를 전달
16x16 feature map 에서 head가 1개인 global attention 사용
각 residual block에 timestep embedding의 projection 해줌

성능향상을 위해, 아키텍처의 변화를 실험하였다.

모델 사이즈는 일정하게 유지하면서, 깊이 증가
attention head 수 증가
16x16 에서 뿐만 아니라 32x32, 8x8에서도 attention 사용
BigGAN의 residual block을 upsampling과 downsamping에 사용
Residual connection 을 $1/\sqrt{2}$ 로 rescale

ImageNet 128x128 로, batchsize 256, sampling step 250을 사용하여 sampling하였고, 여러가지 모델구조에 대한 FID는 표는 아래와 같다.

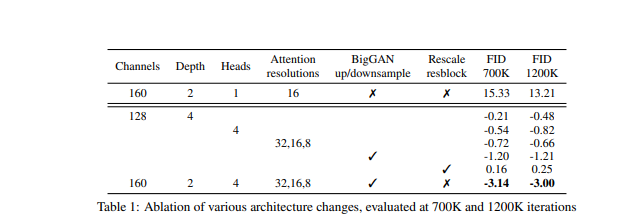
Residaul connection 을 rescale 하는 것을 제외하고, 모두 성능이 개선된 것을 확인 할 수 있다.

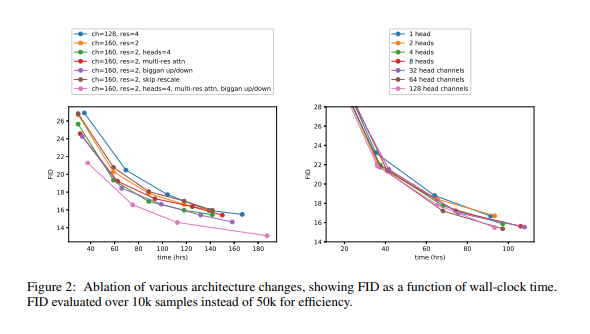
위 그래프에서 볼 수 있듯이, 깊이가 증가하면 성능이 도움이 되지만, train 시간이 늘어나고, 동일한 성능에 도달하는데 더 오랜 시간을 걸리는 것을 관찰할 수 있어서, 추가 실험에서는 이 변경 사항을 적용하지 않기로 했다.

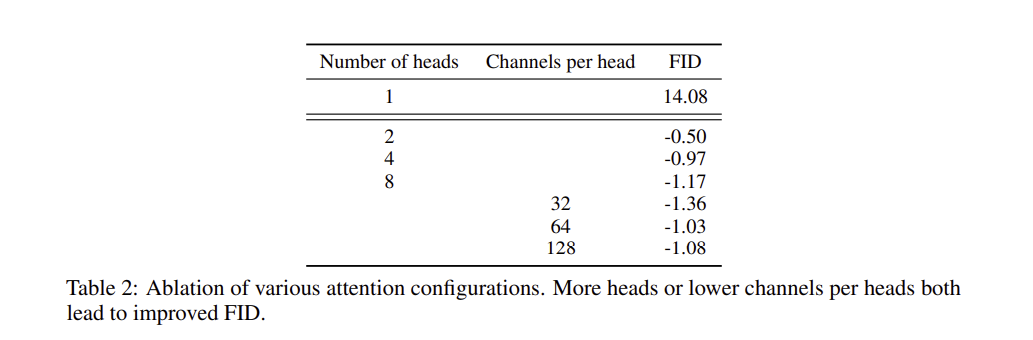
Transformer 구조에서 제안된 attnetion과 더 잘 일치하는 attention 구조에 대한 실험을 진행하였다. Attention head의 수 또는 하나의 head에 전조해는 channel 수를 변화시키며 FID를 측정하였다. head의 수를 늘리거나 channel 수를 줄이는 것이 높은 성능을 나타냄을 알 수 있다.

64채널을 사용하는 경우 시간적인 측면에서 가장 좋은 결과를 나타냈으며, 이후 실험에서도 64 채널을 기본으로 사용한다.

3.1 Adaptive Group Normalization

Adaptive Group Normalization ( AdaGN ) 은 Group Noramlization ( 그룹 정규화 ) 후에 time step 과 class embedding 을 통합하여, 각 residual block에 넣어주는 값에 scaling 과 offset을 적용하는 layer 이다.

AdaGN 을 다음과 같이 나타낼 수 있다.

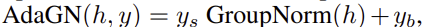
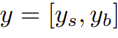
y의 값은 time step 과 class embedding의 linear projection을 통해 얻어진다.
-> Group Normalization을 적용한 값에, $y_s$ 와 $y_b$ 를 적용해준다

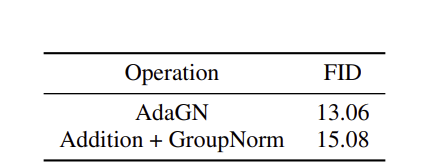
위 표를 보면 AdaGN이 diffusion model의 성능을 개선시키는 것을 확인하였다.

본 논문에서는 다음의 모델 아키텍처를 기본값으로 사용한다.
1. variable width 와 resultion 당 2개의 residual block
2. 64 채널을 가진 multi head의 mutli resolution attention
3. 32,8,16 resolugion 에서 attention
4. BigGAN residual block을 사용한 upsampling과 downsapling
5. timestep embedding 과 class embeding을 Residual block에 주입하기 위한 AdaGN

4 Classifier Guidance

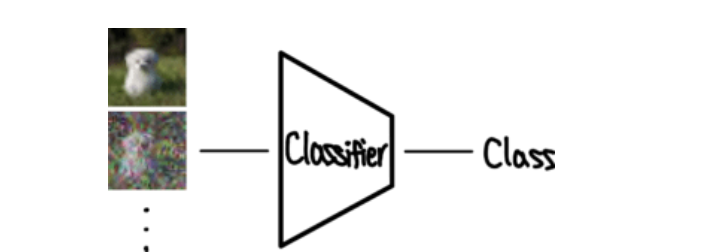
1) Classifier 을 학습해준다. 생성하고자 하는 이미지 데이터셋이 ImageNet이라면, ImageNet Classifier를 학습한다. Diffusion Model 에서 활용하기 위해서, 다양한 Noise Image를 입력 이미지로 넣어준다.

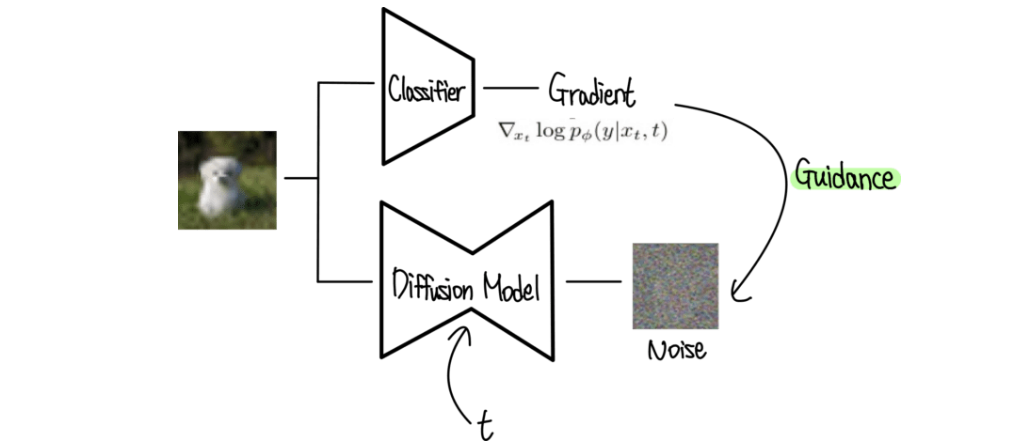
2) Classifier 로부터 입력 이미지에대한 해당 클래스의 gradient 가 예측한 noise 에 추가된다.

-> 이미지는 점차 노이즈가 제거되면서 '강아지' 이미지를 생성한다. 각 단계마다 classifier는 현재 이미지가 ' 강아지' 클래스에 속할 확률을 계산하고, 그 확률을 높이는 방향으로 gradient를 적용하여 이미지를 조정한다. 만약 중간에 이미지가 '고양이' 이미지처럼 보이면, classifier는 '고양이'에 대한 높은 확률을 반환할 것이다. 이경우, '고양이'에서 멀어지고 ' 강아지' 에 가까워지도록 이미지를 조정한다.

4.1 Conditional Reverse Noising Process

Diffusion model 에 classifier $p(y|x_t)$ 를 학습 시키면 더욱 좋은 conditional image synthesis를 할 수 있다. 여기서 classifier는 t 시점의 image를 주어졌을대, 해당 image 에 대한 class가 무엇인지 맞추게하는것이다.

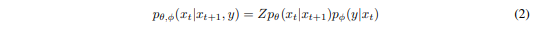
(여기서 Z는 정규화 상수이다.)
위 식 (2) 로 부터, sampling algorithm을 유도한다.

기존의 diffusion model의 p를 (3)과 같이 작성할 수 있다.

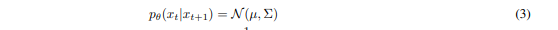
계산의 편의를 위해 log를 씌워주고, Gaussain Distribution의 확률밀도함수를 적용해서 식을 정리하면,

$p(x) = \frac{1}{(2\pi)^{k/2} |\Sigma|^{1/2}} \exp \left( -\frac{1}{2} (x - \mu)^T \Sigma^{-1} (x - \mu) \right)$ 으로 정리할 수 있고, log를 씌워주면

$log p(x) = \log \left( \frac{1}{(2\pi)^{k/2} |\Sigma|^{1/2}} \exp \left( -\frac{1}{2} (x - \mu)^T \Sigma^{-1} (x - \mu) \right) \right)$ 이다.

log 성질에 따라 식을 분해하면, $log p(x) = -\log \left( (2\pi)^{k/2} |\Sigma|^{1/2} \right) - \frac{1}{2} (x - \mu)^T \Sigma^{-1} (x - \mu)$ 과 같고,

$-\log \left( (2\pi)^{k/2} |\Sigma|^{1/2} \right)$ 를 상수 취급하면, (DDPM에서, $\Sigma$ 부분을 상수취급하였다 )

다음과 같이 나타낼 수 있다.

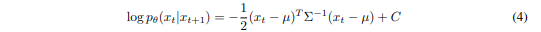
테일러 근사를 활용하여,

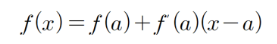
다음과 같이 나타낼 수 있다.

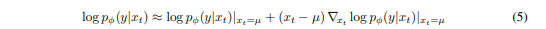
g와 C1을 다음과 같이 정의한다면,

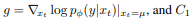
최종적으로 식을 정리하면 다음과 같이 나타낼 수 있다.

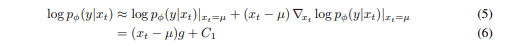
최종적으로, 다음과 같이 식을 근사할 수 있다. 다시 가우시안 분포의 형태로 바꿔줬다.

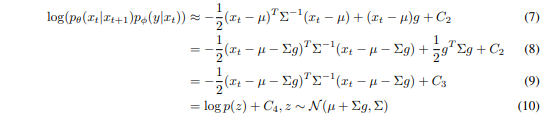
$C_4$ 는 정규화 계수 Z 에 해당하는 상수 항이므로 무시할 수 있고, 평균이 $\Sigma g$ 만큼 이동한 Gaussian 분포로 근사할 수 있음을 알 수 있다.

sampling하는 과정은 다음과 같다.

gradient 에 대해 optional scale factor 's' 를 사용하는데 이는 4.3에서 자세히 다룬다.

4.2 Conditional Sampling for DDIM

4.1 절의 방법은 stochastic sampling 과정에만 적용할 수 있고, DDIM 과 같은 determinisitc sampling 에는 적용될 수 없어서, score-based trick을 제안한다.

$x_t$ 가 Gaussian 분포를 따른다고 가정하면,
확률밀도 함수는 p(x $_t) \propto \exp\left(-\frac{(x_t - \mu_t)^2}{2\sigma_t^2}\right)$ 와 같이 표현할 수 있고,
log 확률 밀도함수는 $\log p(x_t) = -\frac{(x_t - \mu_t)^2}{2\sigma_t^2} + C$ 와 같이 표현할 수 있다.
log 확률 밀도 함수의 gradient를 구하면, $\nabla_{x_t} \log p(x_t) = -\frac{x_t - \mu_t}{\sigma_t^2}$ 이다.

$x_t = \sqrt{\alpha_t} x_0 + \sqrt{1 - \alpha_t} \epsilon$ 여기서 $\epsilon$ 는 평균이 0인 표준 정규분포 노이즈이므로, $x_t$ 의 평균은 $\epsilon$ 를 고려하지 않고, $\mathbb{E}[x_t] = \sqrt{\alpha_t} x_0$ 이다 따라서, $\mu_t = \sqrt{\alpha_t} x_0$ 와 같이 정리 할 수 있다,

$\epsilon$ 의 분산은 1이므로 $\text{Var}(x_t) = \text{Var}(\sqrt{\alpha_t} x_0 + \sqrt{1 - \alpha_t} \epsilon)$ 에서, $x_0$ 는 고정된 값이므로, $\epsilon$ 의 분산만 고려하면 $\sigma_t^2 = 1 - \alpha_t$ 으로 나타낼 수 있다.

최종적으로 대입해보면 아래와 같이 같이 나타낼 수 있다

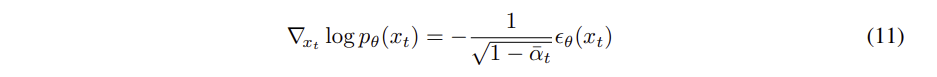
$\nabla_{x_t} \log p_\theta(x_t)$ 은 기본 diffusion 모델의 score 함수이고, $\nabla_{x_t} \log p_\phi(y | x_t)$ 는 조건 y를 고려한 score 함수이다.

score function time t에 대해 다음과 같이 정리할 수 있다.

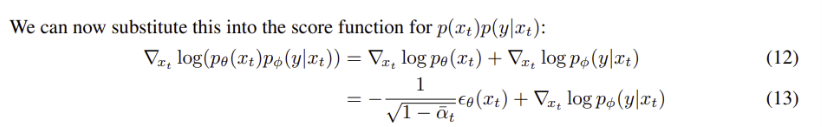
epsilon을 다음과 같이 새롭게 정의할 수 있다.

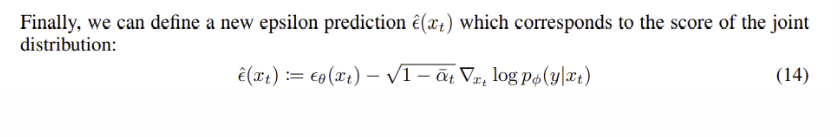
4.3 Scaling Classifier Gradients

Generation task 에 classifier를 적용하기 위해 우선 ImageNet 데이터에 대해 classifier를 학습시킨다. 모델의 구조는 U-net을 기본적으로 사용하며, 8x8의 layer를 downsampling 시켜 classifier 하도록 변형하였다. 원본 이미지에 noise를 추가하여 다양한 수준의 noise 이미지를 생성하고, random crop 을 적용하여여 noise 가 있는 이미지를 분류기에 입력하여 원하는 class로 분류하도록 학습하였다. 학습 후 위의 식 (10) 을 사용하여 diffusion 과 classifier를 결합시켜, sampling 한 이미지가 원하는 class에 속하는지 확률을 계산한다.

classifier 에 의한 gradient 를 1보다 큰 비율로 scaling을 해주어야 한다는 것을 발견하였다. s=1 인 경우 class 에 속할 확률이 약 50 % 였고, sample들이 해당 class에 속하지 않은 경우가 많았다. s>1인 경우에는 특정 class 에 속할 확률이 약 100% 였고, 올바른 sample들이 생성되었다.

아래 사진에서는 왼쪽은 s=1인경우, 오른쪽은 s=10인 경우 이다

scaling 효과를 다음 수식으로부터 설명을 해보면,

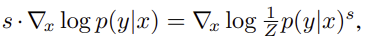
scaling gradient 를 사용하면, $p(y|x) 가 더 sharp해진다. 즉 , 특정 클래스에에 대한 확률이 더 높아지고, 나머지 class에 대한 확률이 더 낮아진다.

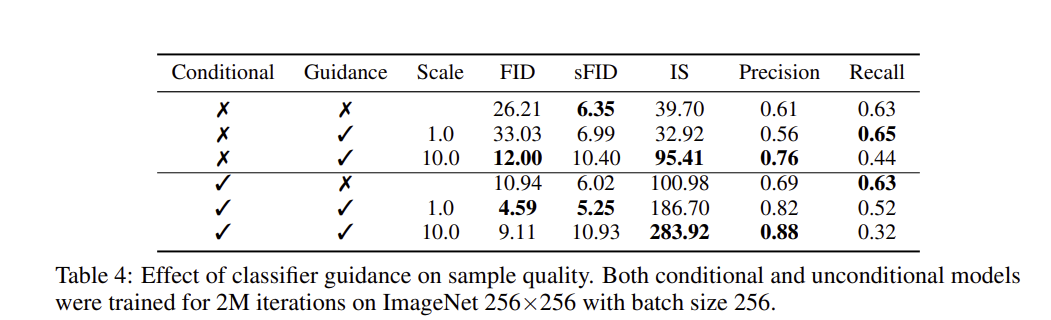
이때까지, diffusion model은 uncoditional model이라고 가정하였으나, diffusion model 자체를 conditional model로 사용할 수 있다. classifer guidance는 동일한 방식으로 적용된다. 모델의 종류와 classifier guidance 유무에 따른 sampling 결과를 위 표에서 확인할 수 있다. conditional model과 guidance를 같이 사용하고 scale 을 키움으로써 가장 좋은 FID 를 얻는 것을 볼 수 있다.

Recall은 diversity를 , Precision 과 IS 는 quality를, FID와 sFID는 diversity와 quality를 종합적으로 고려한 지표이다.

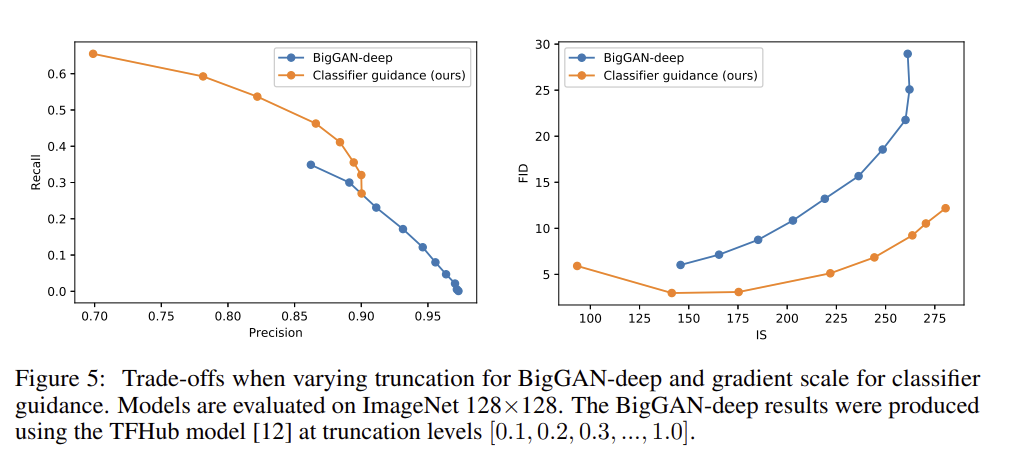
gradient sclae 를 조정하여 precision과 recall, 즉 diversity 와 quality의 trade off 관계를 파악할 수 있다.

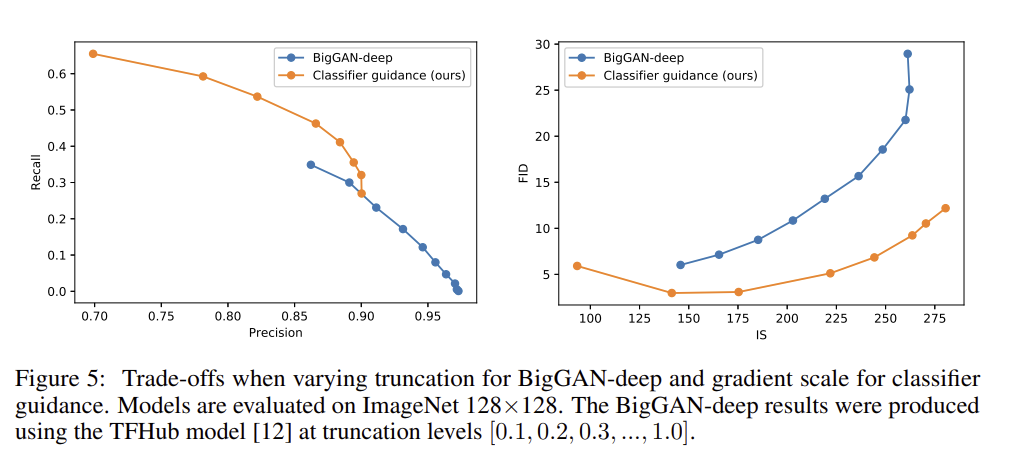
위 그래프는 BigGAN의 truncatioj tirck과 classifier guidance를 비교한다. FID, IS를 고려했을때, classifier guidance 가 BigGAN 보다 훨씬 나은 것을 확인 할 수 있다. Precision/recall trade off그래프는 classifier guidance가 특정 precision 값 까지만 나은 선택이며, 그 이후에는 더 나은 precision을 달성할 수 없다.

5 Results

unconditional image generation 평가를 위해 LSNU 데이터셋에서 bedroom, horse, cat 세가지 class 에 대해서 각각 학습시켜 이미지를 생성하였다. Classifier guidance의 평가를 위해 ImageNet의 128x128, 256x256, 512x512 크기에 대하여 conditional diffusion model을 학습시켰다.

5.1 State-of-the-art Image Synthesis

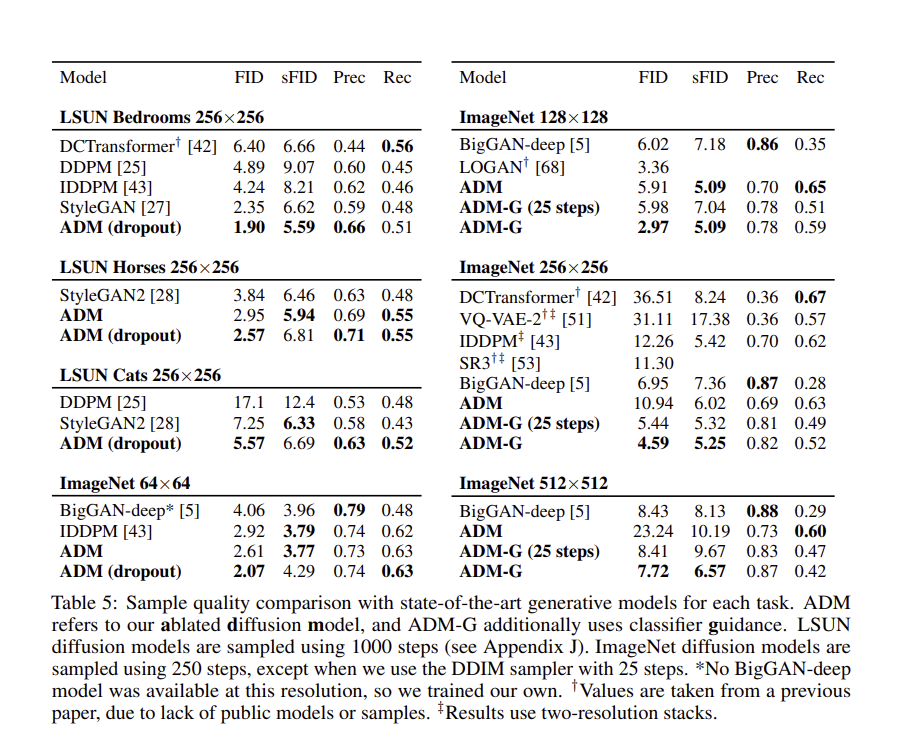
Ablated Diffusion Model ( ADM ) 에 대한 실험 결과에 대한 표이다. 모든 task에 대해 가장 좋은 FID를 달성하며, 1개의 task를 제외하고도 가장 좋은 sFID 를 달성한다. 더 높은 해상도의 ImageNet 에 대해서는 classifer guidance를 통해 GAN 보다 더 높은 품질의 이미지를 생성한다.

위 사진의 1열은 BigGAN-deep 모델에 의해서 생성된 sample 이며, 2열은 가장 성능이 좋았던 ADM-G에 의해 생성된 sample 이며, 3열은 원본 이미지 데이터이다.
이미지의 qulity는 비슷하지만 ADM-G 가 더 다양한 이미지를 sampling 한 것을 확인 확인 할 수 있다.

5.2 Comparison to Upsampling

low resolution diffusion model 과 upsampling diffusion model을 결합하여 이미지를 생성하는 방법이 제시 되었는데, low resolution model은 sample을 생성하고, upsampling model은 해당 sample에 대해 upsmapling을 수행한다. 이 기법을 통해 256x256 image에 대한 FID score를 개선시켰지만, BigGAN-deep 만큼의 quality는 얻지 못했다.

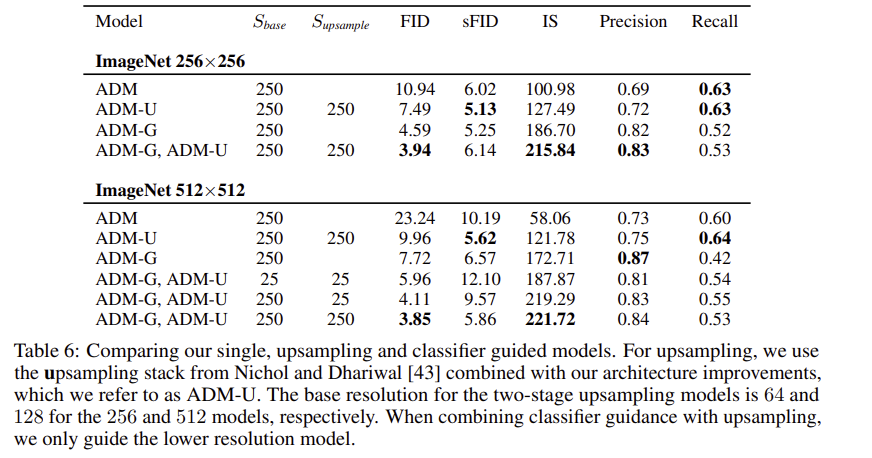
위 표는 upsapling model과 guidance model을 비교한 표이다. guidance와 upsampling이 서로 다른 방향으로 sample의 품질을 향상시키는 것을 확인할 수 있다. upsampling은 recall을 높게 유지한 채로 precision을 개선하며, guidance는 높은 precision을 위해 diversity를 포기한다.