이론으로만 배웠던 머신러닝을 직접 코랩을 이용해 구현해보았다.
혼자공부하는 머신러닝-딥러닝책에 나온 예제를 통해 생선 분류 문제를 해결해보았으며 k-최근접 이웃 알고리즘을 사용해서 해결하였다.
먼저 가장 중요한 데이터셋.
도미와 빙어를 분류하기 위해서는 각 생선의 무게와 길이를 알아야 한다.
bream_length = [25.4, 26.3, 26.5, 29.0, 29.0, 29.7, 29.7, 30.0, 30.0, 30.7, 31.0, 31.0,
31.5, 32.0, 32.0, 32.0, 33.0, 33.0, 33.5, 33.5, 34.0, 34.0, 34.5, 35.0,
35.0, 35.0, 35.0, 36.0, 36.0, 37.0, 38.5, 38.5, 39.5, 41.0, 41.0]
bream_weight = [242.0, 290.0, 340.0, 363.0, 430.0, 450.0, 500.0, 390.0, 450.0, 500.0, 475.0, 500.0,
500.0, 340.0, 600.0, 600.0, 700.0, 700.0, 610.0, 650.0, 575.0, 685.0, 620.0, 680.0,
700.0, 725.0, 720.0, 714.0, 850.0, 1000.0, 920.0, 955.0, 925.0, 975.0, 950.0]
위의 길이와 무게는 35마리의 도미의 데이터이다. 위의 데이터를 통해 육안으로 보기 쉽게 x축을 길이, y축을 무게로 하여 산점도를 그려보았다.
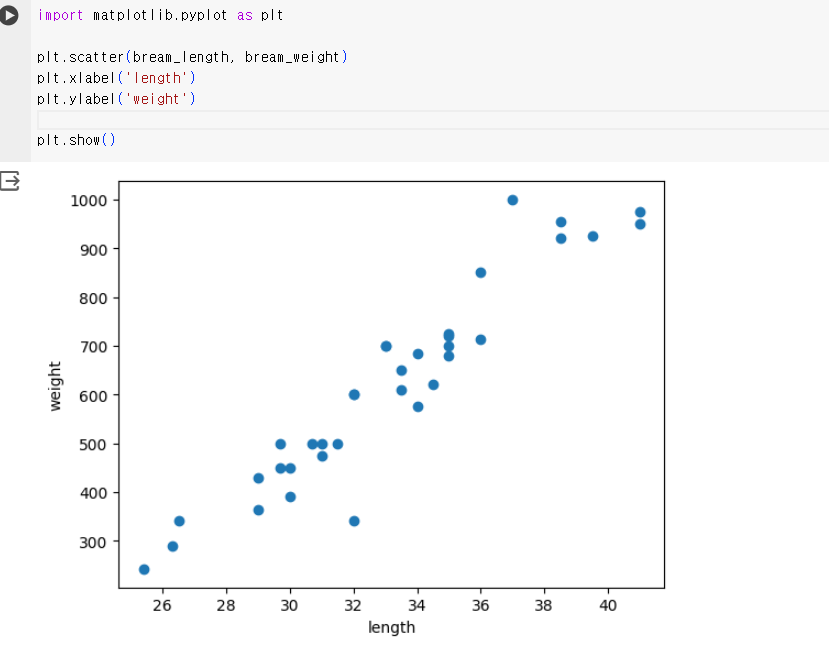
생선의 길이가 길수록 무게가 많이 나간다고 생각하면 위 그래프의 모습은 매우 자연스럽다. 선점도 그래프가 일직선에 가까운 형태로 나타나는 경우를 선형적이라고 말한다.
다음은 빙어의 데이터이다.
smelt_length = [9.8, 10.5, 10.6, 11.0, 11.2, 11.3, 11.8, 11.8, 12.0, 12.2, 12.4, 13.0, 14.3, 15.0]
smelt_weight = [6.7, 7.5, 7.0, 9.7, 9.8, 8.7, 10.0, 9.9, 9.8, 12.2, 13.4, 12.2, 19.7, 19.9]빙어는 도미와 다르게 길이와 무게가 많이 나가는 편이 아니다. 준비한 데이터는 14마리이며 각각 길이와 무게를 보인 결과이다. 도미와 빙어의 선점도를 한 그래프로 표현하면 다음과 같다.
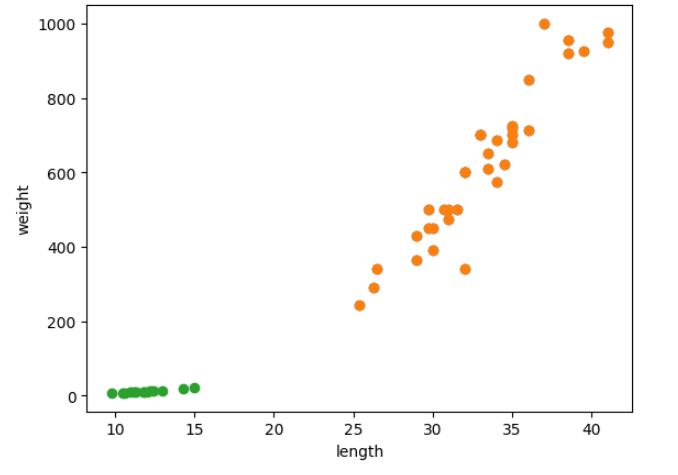
언뜻 보기에도 차이가 많이 나는 것으로 볼 수 가 있다. 이제 본격적으로 도미와 빙어의 데이터를 분류하기 위해서 간단하게 두 리스트를 하나로 합쳤다.
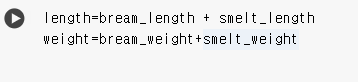
2차원 리스트를 만든 후에 파이썬의 zip()함수와 리스트 내포구문을 사용한다. zip()함수는 나열된 리스트 각각에서 하나씩 원소를 꺼내 반환한다. zip()함수와 리스트 내포 구문을 사용해 length와 weight리스트를 2차원 리스트로 만들면

위와 같다.
머신러닝은 물론이고 컴퓨터는 문자를 직접 이해하지 못한다. 대신 도미와 빙어를 숫자 1과 0으로 표현하여 분류할 수 있다.

1이 35번 등장하고 0은 14번 등장한걸 볼 수 있다.
이제 우리가 구하고자 하는 새로운 크기와 무게가 주어졌을 때 이것이 도미인지, 혹은 빙어인지 알고 싶을 경우가 있을 것이다. KNeighborsClassifier를 임포트하여 객체를 만든 후에 훈련을 진행한다.

만든 객체에 fish_data와 fish_target을 전달하여 도미를 찾기 위한 기준을 학습시킨다. fit()메서드가 이런 역할을 하며 모델을 평가하는 score()메서드를 추가한다. 여기서 1은 모든 데이터를 정확히 맞혔다는 것이고 0.5면 반만 맞혔다는 뜻이다.
k-최근접 이웃 알고리즘을 이용해서 길이가 17이고 무게가 820인 생선의 종류를 알고 싶다. 정말 특이한 케이스지만 없을 거라는 장담은 못한다. 육안으로 볼때는 길이는 빙빙어인데 무게로 보면 도미와 같다.
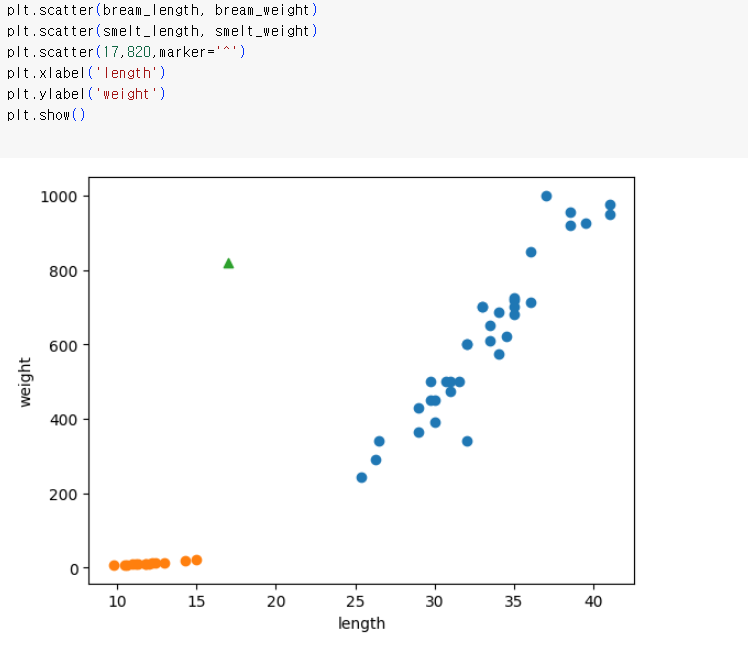
세모로 표시된 곳이 내가 구하고자 하는 생선의 크기와 무게이다.
정답은?
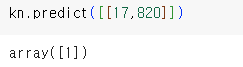
1 즉 도미이다. default로 설정된 5개의 데이터의 거리를 획득해서 가장 가까운 1번 도미와 비슷하다고 판단이 난 것이다. 만약에 가까운 5개가 아니라 모든 데이터 49개의 거리를 계산해서 얻고 싶으면

이는 기본값 5로 하는 것보다 좋지 않은 결과가 나왔다. 도미를 완벽하게 분류한 모델인 기본값 5로 설정하여 하는 것이 좋아 보인다.
