딥러닝 학습 : 문제점과 해결 방안 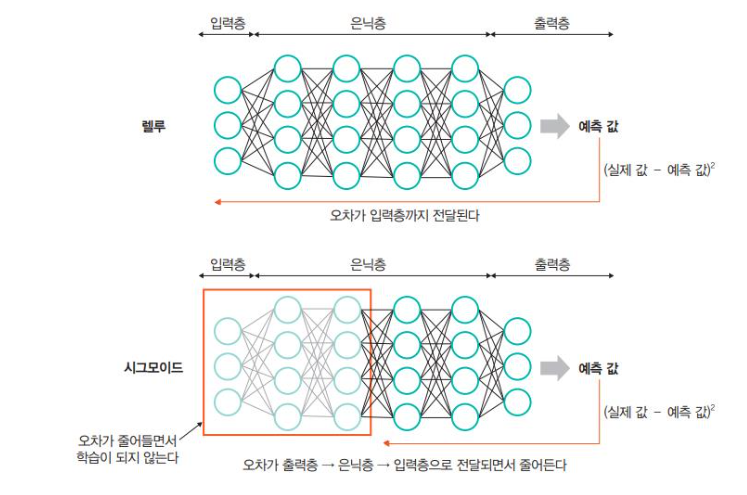
서능 저하 문제
경사 하강법은 손실 함수의 비용이 최소가 되는 지점을 찾을 때까지 기울기가 낮은 쪽으로 계속 이동시키는 과정을 반복 함. 이때 선능이 나빠지는 문제가 발생함.
경사 하강법
Gradient
-> 수학적으로 연산의 변화율 -> 다차원 입력을 받은 함수에 변화율 개념의 확장
Local gradient
->기존의 수식을 통해 구할 수 있는 gradient
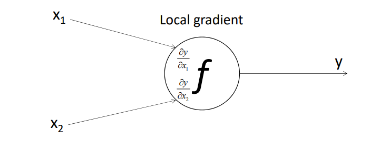
Global gradient
->뒤에서부터 앞으로 넘어오는 gradient
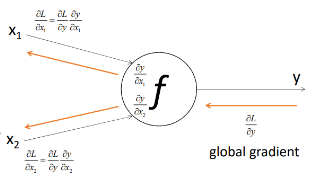
Gradient Descent
: 1차 미분 계수를 이용해 함수의 최소값을 찾아가는 과정임
비용함수(cost function)의 비용 값을 최소화하는 파라미터θ를 찾는 과정임.
그러나, 최소값인 지점을 짐작하기 어렵기 때문에 기울기를 이용하여 최솟값을 찾으려는 과정이 경사 하강법임.
함수 기울기를 낮은 쪽으로 계속 이동시켜 극 값에 이를 때까지 반복함.
제시된 함수의 기울기로 최소값을 찾아내는 머신러닝 알고리즘임.
비용함수를 최소화하기 위해 매개 변수를 반복적으로 조정하는 과정임.
학습을 통해 최적의 파라미터 값을 찾는 것이 목표임.
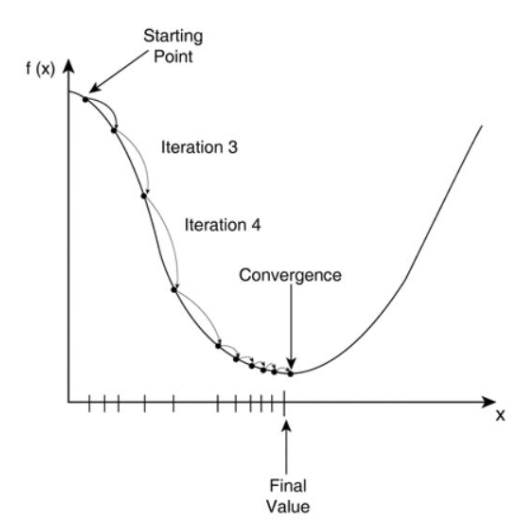
Gradient Descent 과정
1. 특정 파라미터 값으로 시작 : 가중치 w1에 대한 시작 값을 선택함.
2. Cost function 계산 : 시작점에서 곡선의 기울기 계산
3. 파라미터 값 업데이트
4. 반복 학습 : n번의 iteration으로 진행되고, 최소값을 향하여 수렴함.
배치 경사하강법, 확률적 경사 하강법, 미니 배치 경사 하강법
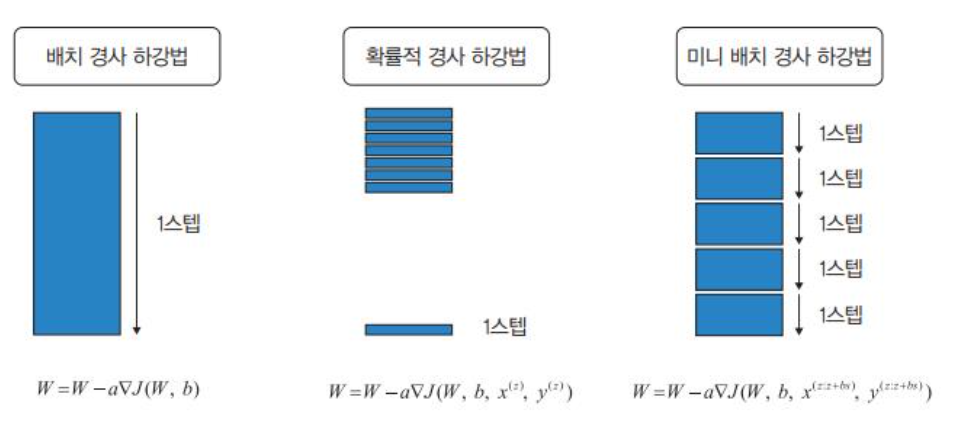
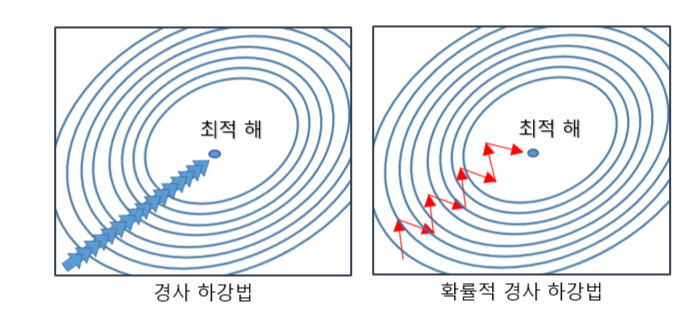
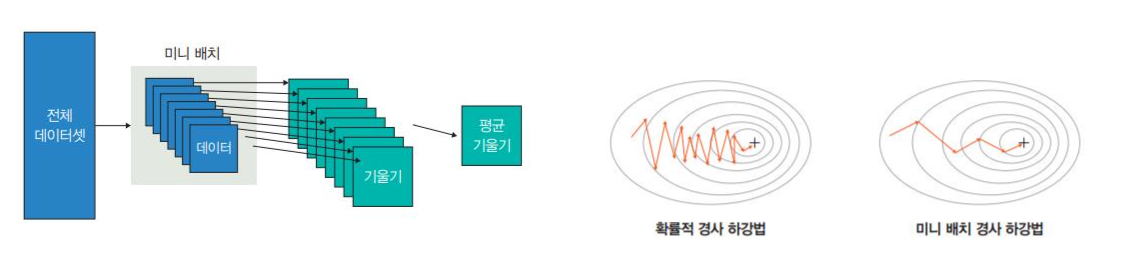
확률적 경사 하강법 ->
추출된 데이터 한 개에 gradient를 계산하고 경사 하강 알고리즘을 적용하는 방법임
랜덤하게 추출한 일부 데이터를 사용함.
학습 중간 과정에서 결과의 진폭이 크고 불안정하며, 속도가 매우 빠름.
미니배치 경사 하강법->
전체 데이터를 batch_size개씩 나눠 배치로 학습(batch_size는 일종의 하이퍼파라미터)
평균 기울기를 통해 모델을 업데이트함.
이때, 배치 크기를 사용자가 지정함.
ex)전체 데이터가 1000개인 데이터를 학습시킬 때, batch size가 100이면 총 10개의 batch가 생성되는 것이며 1Epoch당 10번 iteration이 생김.
경사 하강법을 파이토치에서 구현
class CustomDataset(Dataset):
definit(self):
self.x_data=[[1,2,3],[4,5,6],[7,8,9]]
self.y_data=[[12],[18],[11]]
def__len__(self):
return len(self.x_data)
def__getitem__(self,idx):
x=torch.FloatTensor(self.x_data[idx])
y=torch.FloatTensor(self.y_data[idx])
return x,y
dataset=CustomDataset()
dataloader=dataLoader(
dataset, //데이터셋
batch_size=2, //미니 배치 크기로 2의 제곱수를 사용하겠다는 의미임.
shuffle=True, //데이터를 불러올 때마다 랜덤으로 섞어서 가져옴.
딥러닝 학습: 옵티마이저
옵티마이저(Optimizer)
확률적 경사 하강법의 파라미터 변경 폭이 불안정한 문제를 해결하기 위해 학습 속도와 운동량을 조정함.
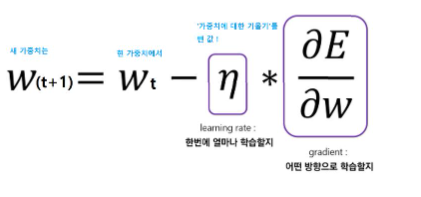
Gradient Descent 과정에서의 학습률
n : 갱신하는 양-> 신경망 학습에서 학습률이라고 함.
학습률은 하이퍼파라미터라고 부르며 가중치와 편향같은 신경망의 매개변수와는 다름.
수동적으로 설정해야하기 때문에 실함을 통해 적절한 값을 찾아가야 함.
1회에 해당하는 갱신, 단계 반복
변수의 값을 갱신하는 단계를 여러 번 반복하면서 서서히 함수의 값을 줄임
여기서는 변수 2개인 경우이지만, 변수의 수가 늘어도 같은 식(=각 변수의 편미분 값)으로 갱신함.
여기서는 변수 2개인 경우이지만, 변수의 수가 늘어도 같은 식(=각 변수의 편미분 값)으로 갱신.
학습률 값은 0.01이나 0.001등 미리 특정 값으로 설정해야함.
신경망 학습에서는 보통 이 학습률을 변경하면서 올바르게 학습하고 있는지 확인하면서 진행함.
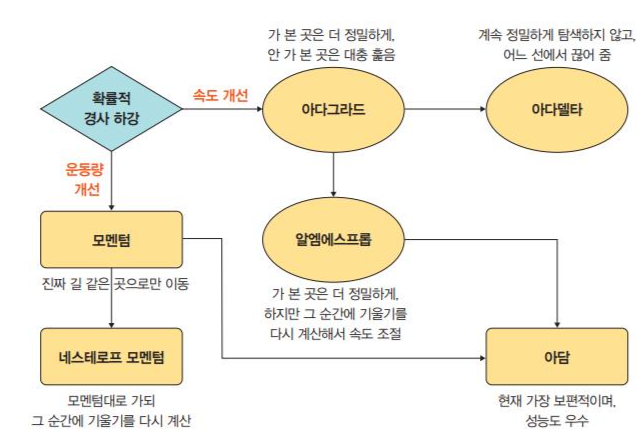
학습률이 너무 크면 큰 값을 반환하고, 너무 작으면 거의 갱신되지 않고 종료가 됨.
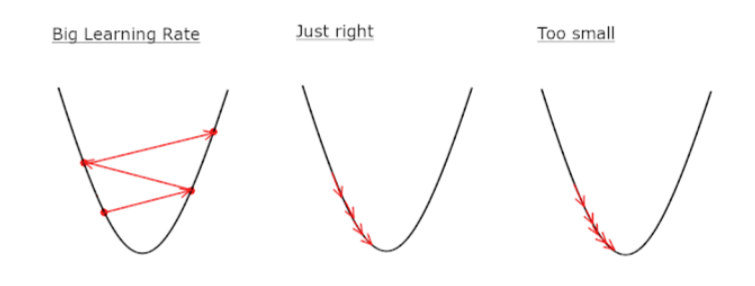
모멘텀(Momentum)
기울기에 관성을 부과하여 작은 기울기는 쉽게 넘어갈 수 있도록 만든 것을 말함.
신경망의 학습 안정성과 속도를 높여 학습을 잘 되게 하려는 것을 말함.
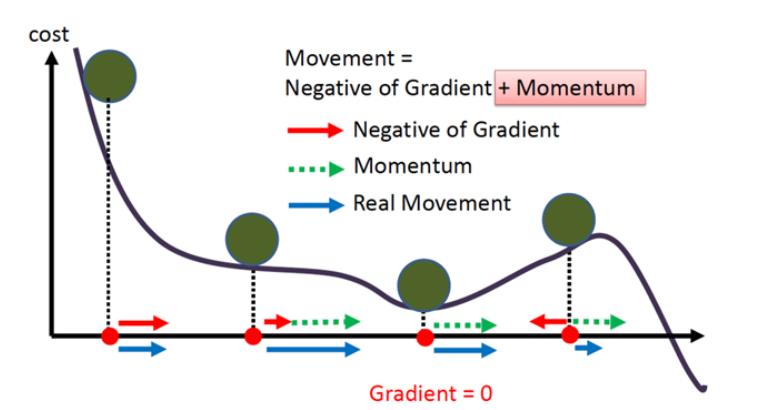
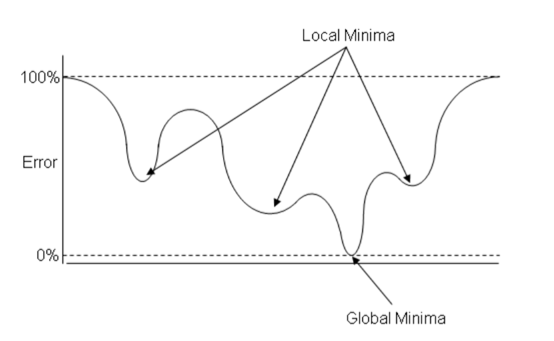
경사 하강법은 현재 위치에서의 기울기를 사용하기 때문에 지역 최소값에 빠질 수 있음.
무작위 초기화ㅑ(random initialization)으로 지역 최소값에 수렴할 수 있음.
평탄한 지역을 지나가기 위해 오랜 시간이 걸리고 일찍 멈추어 전역 최소값에 도달하지 못할 수가 있음.
모멘텀으로 이와 같은 문제를 해결함.