지도학습은 정답(레이블/label)을 컴퓨터에 미리 알려 주고 데이터를 학습시키는 방법.
지도 학습에는 분류와 회귀가 있음.
분류: 주어진 데이터를 정해진 범주에 따라 분류
회귀 : 데이터의 특성을 기준으로 연속된 값을 그래프로 표현하여 패턴이나 트렌드 예측.
최근접 이웃
왜 사용할까? -> 주어진 데이터에 대한 부류를 위해서!
언제 사용하면 좋을까? -> k-최근접 이웃은 직관적이며 사용하기 쉽기 때문에 초보자가 쓰면 좋고 훈련 데이터를 충분히 확보할 수 있는 환경에서 사용하면 더욱 더 좋다.
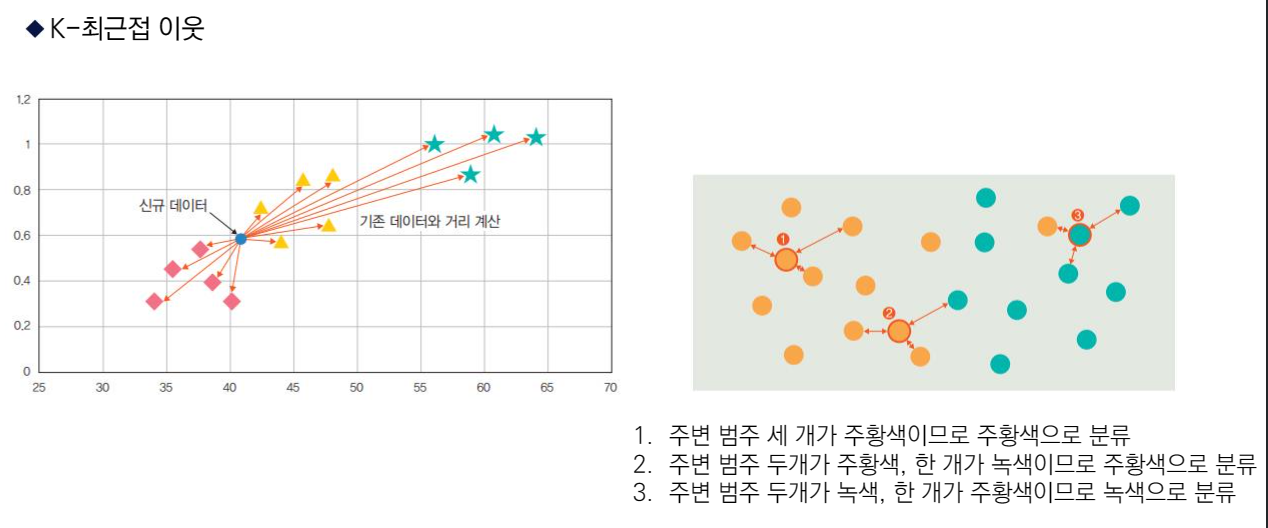
새로운 입력(학습에 사용하지 않은 새로운 데이터)을 받았을 때 기존 클러스터에서 모든 데이터와 인스턴스 기반 거리를 측정한 후 가장 많은 속성을 가진 클러스터에 할당하는 분류 알고리즘.
즉, 과거 데이터를 사용하여 미리 분류 모형을 만드는 것이 아니라, 과거 데이터를 저장해 두고 필요할 때마다 비교를 수행하는 방식.
k 값의 선택에 따라 새로운 데이터에 대한 분류 결과가 달라질 수 있음에 유의해야함.
k-최근접 이웃 예제
목표 : 적정한 k값에 대한 예측
분석 절차 : 라이브러리 호출->데이터셋 로딩->훈련과 검즘 데이터셋 분리-> 모델 생성-> k값 예측
SVM / 서포트 벡터 머신
왜 사용할까? -> 주어진 데이터에 대한 분류
언제 사용하면 좋을까? -> 서포트 벡터 머신은 커널만 적절히 선택한다면 정확도가 상당히 좋기 때문에 정확도를 요구하는 분류 문제를 다룰 때 사용하면 좋고 텍스트를 분류할 때도 많이 사용함.
분류를 위한 기준선을 정의하는 모델이며 즉, 분류되지 않은 새로운 데이터가 나타나면 결정 경계(기준선)를 기준으로 경계의 어느 쪽에 속하는지 분류하는 모델임.
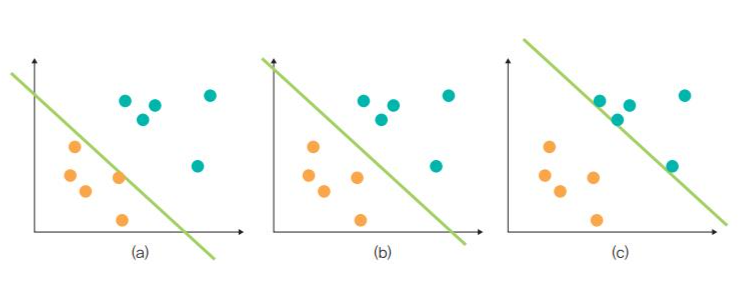
서포트벡터 머신에서 결정 경계는 데이터가 분류된 클래스에서 최대한 멀리 떨어져 있을 때 성능이 좋음.
마진(margin) 은 결정 경계와 서포트 벡터 사이의 거리를 의미함.
서포트 벡터는 결정 경계와 가까이 있는 데이터들을 의미함.
즉, 최적의 결정 경계는 마진을 최대로 해야함을 의미.
서포트 벡터 머신에서 비선형에 대한 커널은 선형으로 분류될 수 없는 데이터들 때문에 발생함.
비선형 문제를 해결하는 가장 기본적인 방법은 저차원 데이터를 고차원으로 보내는 것임.
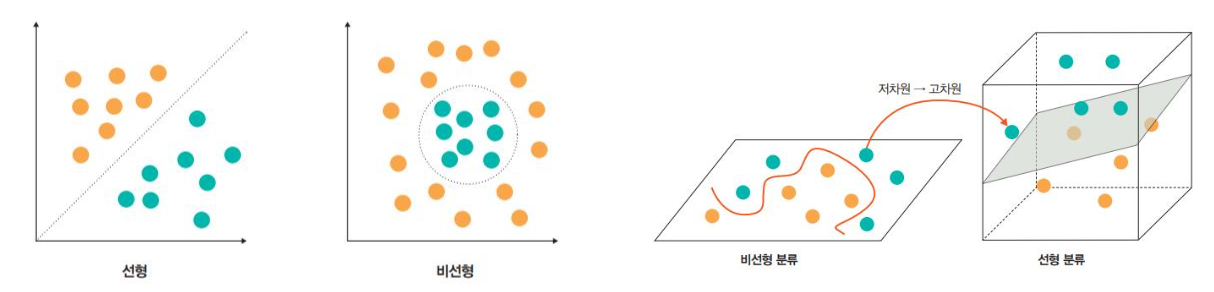
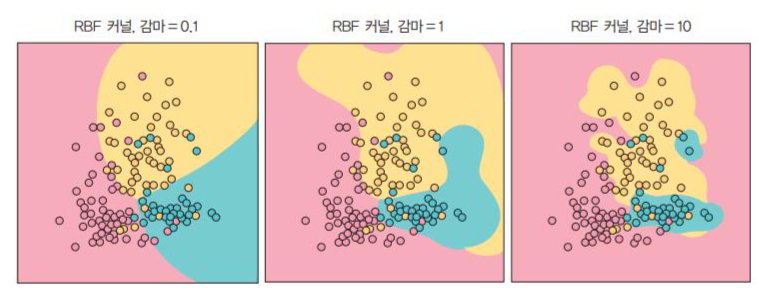
가우시안 BRF 커널
입력 벡터를 차원이 무한한 고차원으로 매핑하는 것을 의미.
모든 차수의 모든 다항식을 고려함.
SVM = svm.SVC(kernel='linear',C=10,gamma=0.5)
결정트리 (Decision Tree)
왜 사용할까? -> 주어진 데이터에 대한 분류
언제 사용하면 좋을까? -> 결정 트리는 이상치가 많은 값으로 구성된 데이터셋을 다룰 때 사용하면 좋으며 결정 과정이 시각적으로 표현되기 때문에 머신 러닝이 어떤 방식으로 의사 결정을 하는지 알고 싶을 때 유용함.
데이터를 1차로 분류한 후에 각 영역의 순도(homogeneity)는 증가하고 불순도(impurity)와 불확실성(uncertainty)은 감소하는 방향으로 학습을 진행함.
순도가 증가하고 불확실성이 감소하는 정보 이론에서는 정보 획득이라고 하며, 순도를 계산하는 방법에는 다음 두가지를 많이 사용함. ->엔트로피와 지니계수

엔트로피 / entropy
확률 변수의 불확실성을 수치로 나타낸 것으로 엔트로피가 높을수록 불확실성이 높다는 의미.
엔트로피=0=불확실성 최소=순도 최대
엔트로피=0.5=불확실성=순도 최소
지니게수/Gini index
불순도를 측정하는 지표로 데이터의 통계적 분산 정도를 정량화해서 표현하는 값
즉, 지니 계수는 원소 n개 중에서 임의로 두 개를 추출했을 때, 추출된 두개가 서로 다른 그룹에 속해 있을 확률을 의미.
지니 계수가 높을수록 데이터가 분산되어 있음을 의미.
엔트로피보다 계산이 빠르기 때문에 결정 트리에서 많이 사용함.
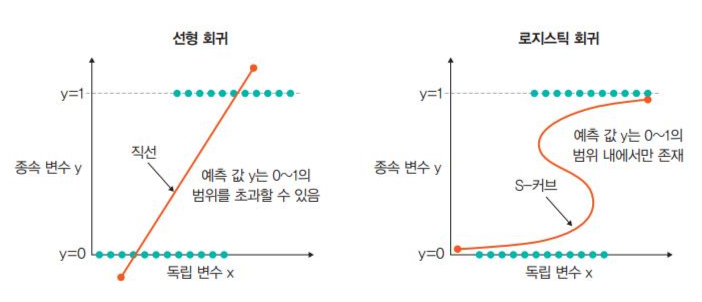
로지스틱 회귀/Logistic Regression
왜 사용할까? -> 주어진 데이터에 대한 분류
언제 사용하면 좋을까? -> 로지스틱 회귀 분석은 주어진 데이터에 대한 확신이 없거나(예를 들어 분류 결과에 대해 확신이 없을 때)향후 추가적으로 훈련 데이터셋을 수집하여 모델을 훈련시킬 수 있는 환경에서 사용하면 유용함.
분석하고자 하는 대상들이 두 집단 혹은 그 이상의 집단으로 나누어진 경우, 개별 관측자들이 어느 집단으로 분류될 수 있는지 분석하고 이를 예측하는 모형을 개발하는 데 사용하는 통계 기법임.
선형 회귀/Linear Regression
왜 사용할까? -> 주어진 데이터에 대한 분류
언제 사용하면 좋을까? -> 로지스틱 회귀는 주어진 데이터에서 독립 변수(x)와 종속 변수(y)가 선형 관계를 가질 때 사용 하면 유용함. 또한 복잡한 연산 과정이 없기 때문에 컴퓨팅 선능이 낮은 환경 혹은 메모리 성능이 좋지 않을 때에 사용하면 좋음.
독립 변수 x를 사용하여 종속 변수 y의 움직임을 예측하고 설명하는 데 유용.
독립 변수는 여러 개일 수도 있음.
하나의 x로 y를 설명할 수 있다면 단순 선형 회귀(simple linear regression)
x가 여러 개라면 다중 선형 회귀(multiple linear regression)
회귀 모델
선형 회귀 vs 로지스틱 회귀
선형 회귀는 독립 변수가 변경되었을 때 종속 변수르 추정하는데 유용함.
로지스틱 회구는 사건의 확률(0또는 1)을 확인하는 데 사용.