최소 신장 트리(Minimum Spanning Tree)
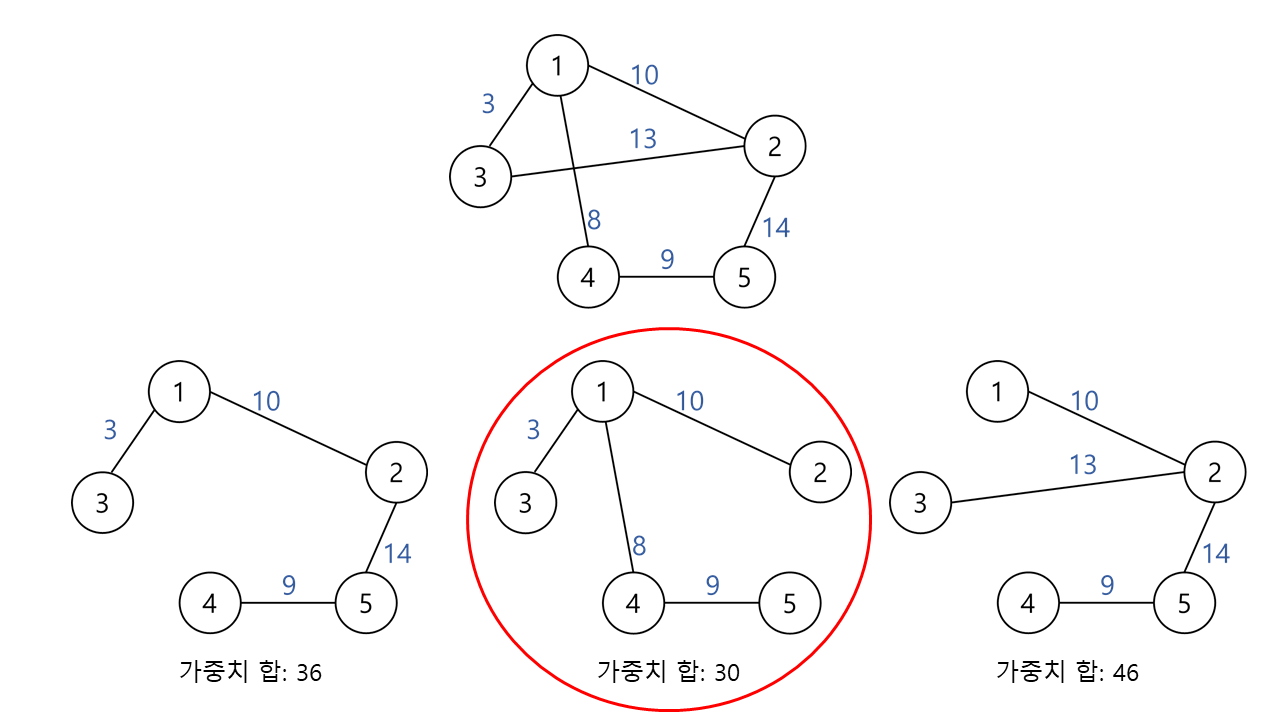
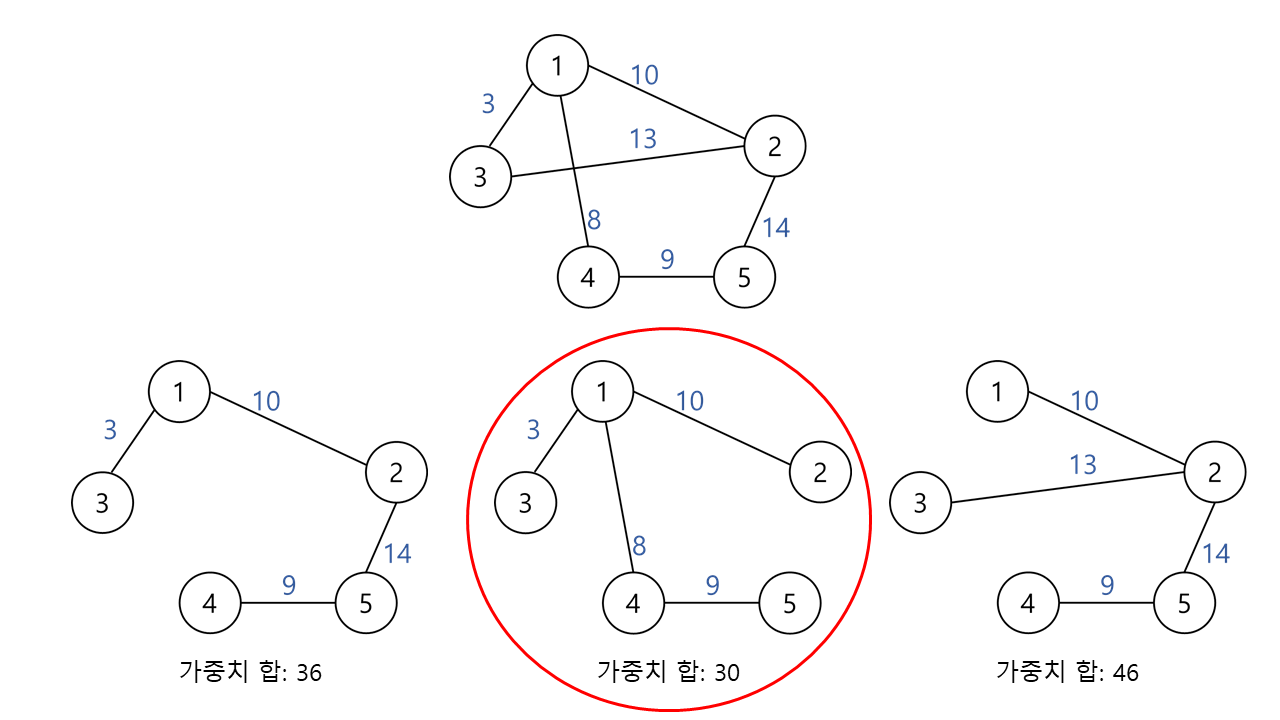
MST, 최소 신장 트리란 그래프에서 모든 노드를 연결할 때 사용된 에지들의 가중치의 합을 최소로 하는 트리이다.
MST를 구현하는 대표적인 방식 두 가지는 '크루스칼'과 '프림'이 있다. MST는 다음과 같은 특징을 지닌다.
MST는 사이클이 포함되면 가중치의 합이 최소가 될 수 없으므로 사이클을 포함하지 않는다. N개의 노드가 있을 시, 에지의 개수가 N개가 되면 모든 노드를 연결하는 사이클이 생성되므로, N개의 노드가 있을 때 MST를 구성하는 에지의 개수는 항상 N-1개다.
MST 핵심 이론 - Kruskal’s Algorithm
1. 에지 리스트로 그래프를 구현하고 Union find 리스트 초기화
MST는 데이터를 노드가 아닌 에지 중심으로 저장해야 하므로 에지 리스트를 사용하여 그래프를 구현한다.
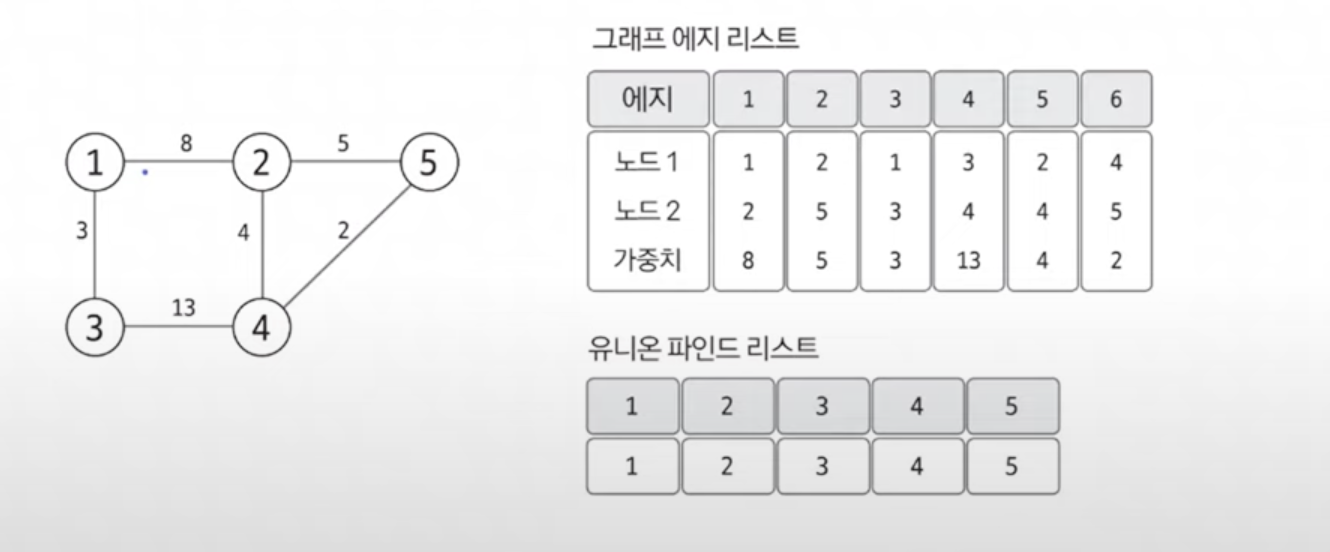
에지 리스트로 그래프를 구현한 후에 'union find'로 리스트를 초기화하는 이유는, 사이클을 판별해내기 위해서이다. 따라서 MST를 구현하기 위해서는 기본적으로 Union find 알고리즘의 동작원리를 이해하고 있어야 한다. 초기화는 리스트의 인덱스를 해당 자리의 값으로 설정하여 초기화하면 된다.
2. 데이터를 가중치 기준으로 정렬
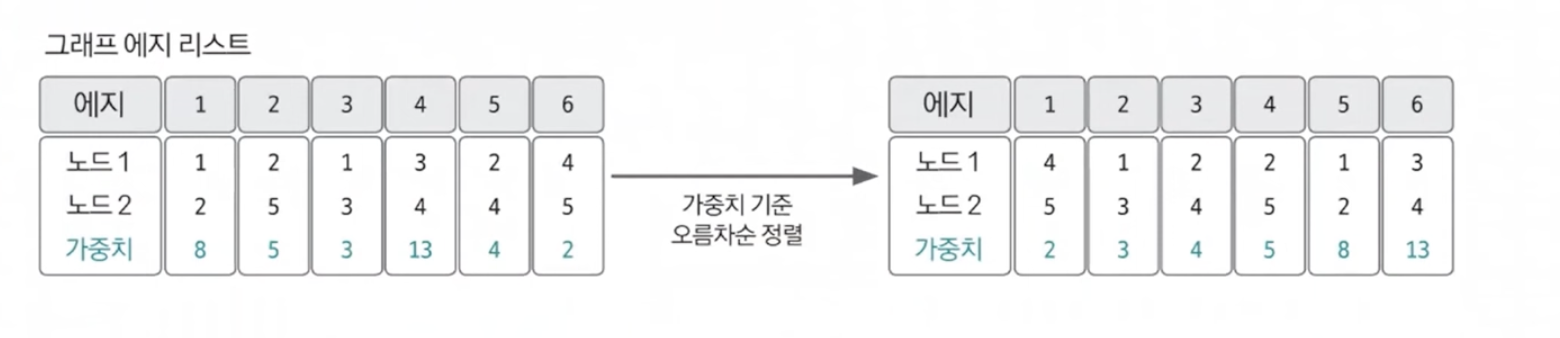
그래프 데이터를 가중치 기준 오름차순 정렬한다.
3. 가중치가 낮은 에지부터 연결 시도 & 반복
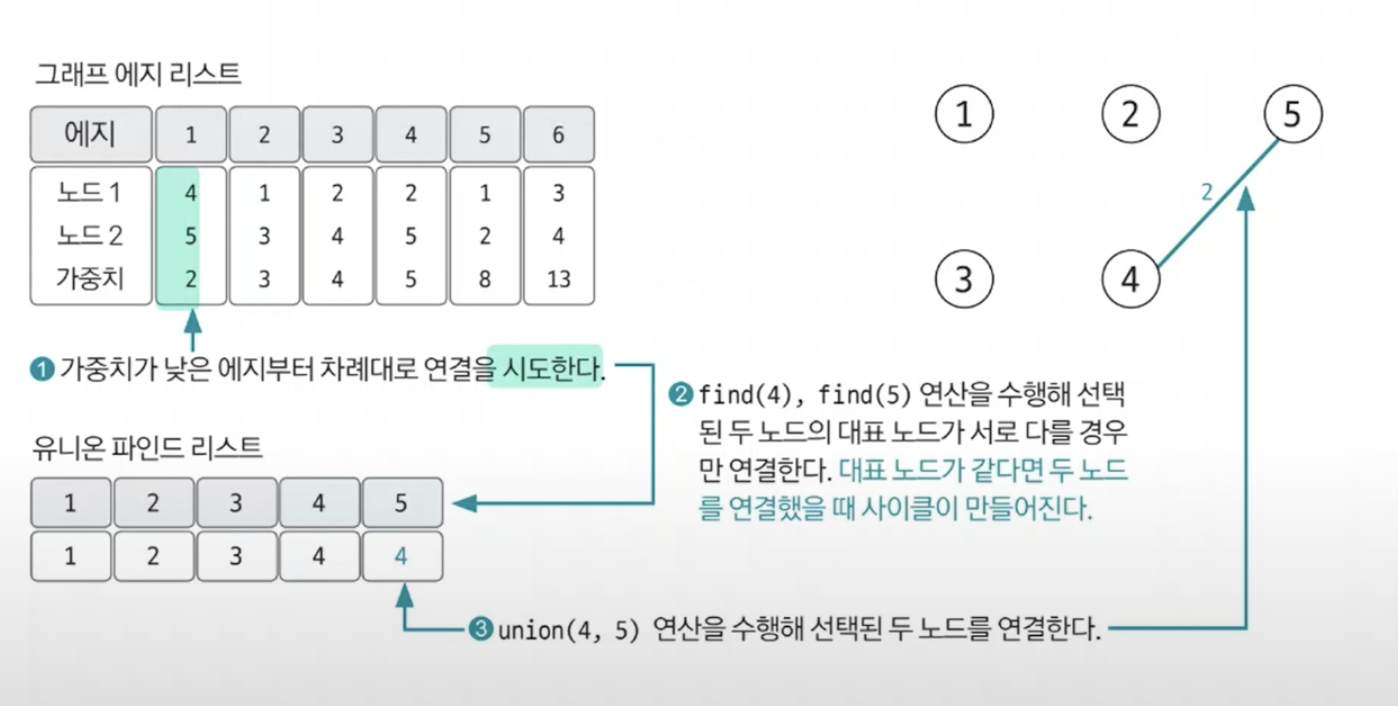
매 연결 시도마다 find연산을 수행해서 대표 노드가 같은지 다른지 여부를 확인해 사이클 생성여부를 확인한 후 연결한다!
위의 글처럼, find연산을 수행시켰을 때 대표 노드가 같지 않을 경우에 연결을 하고, 후에 Union 연산을 수행해 Union find 리스트를 수정시킨다. 반복하는 과정은 아래와 같다.
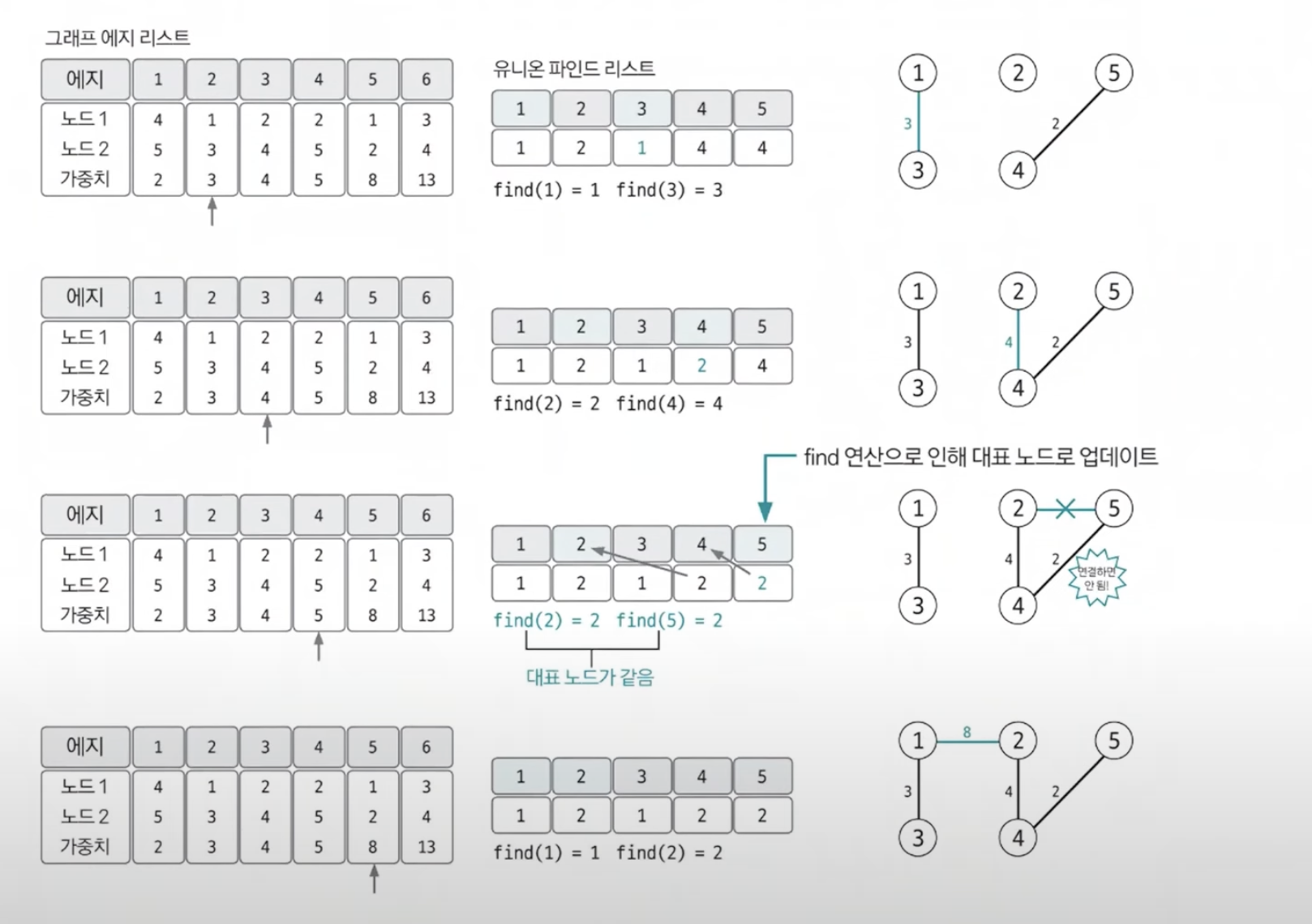
위의 예시에서는 에지 4가 유니온 연산에서 사이클이 생성되서 에지 4는 연결 시도가 실패한다. 이렇게 모든 연산을 수행했을 때 에지의 개수가 노드의 개수 -1이라는 것을 위의 예시를 통해서도 확인할 수 있다.
4. 총 에지 비용 출력
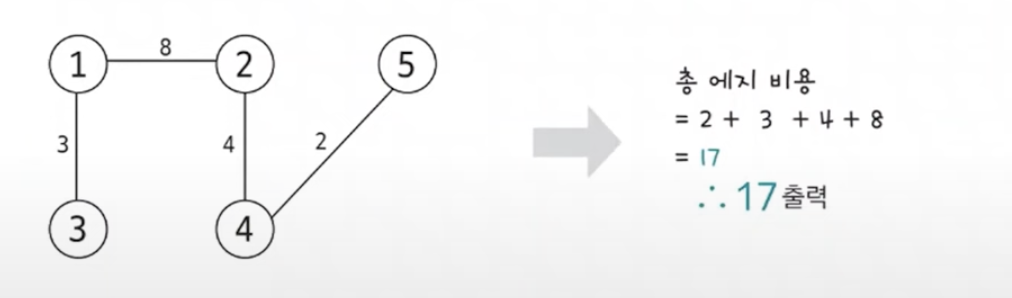
총 에지의 개수가 N-1이 되면, 알고리즘을 종료하고 총 가중치의 합을 출력한다.
