[Algorithm] 07. Brute-Force algorithm

Brute force algorithm이란?

Brute(무식한), Force, 즉, 무식한 힘을 가진 알고리즘이란 뜻으로, 가능한 모든 경우의 수를 모두 탐색하며 결과를 도출하는 알고리즘

말 그대로, 무식하게 가능한 모든 경우의 수를 탐색하는 알고리즘으로서, 전체 탐색 또는 완전 탐색이라고도 부른다. 대부분의 경우 반복문과 조건문을 통하여 결과를 도출해낸다. 대표적인 예시로, 숫자 자물쇠를 들 수 있다. 가능한 모든 숫자 조합을 하나씩 시도해보는 것, 이때 브루트 포스 알고리즘이 활용된다.

알고리즘을 구현하기가 비교적 쉽고, 모든 경우의 수를 탐색하는 알고리즘이기에 정확성 100%를 보장한다는 확실한 장점이 있다. 하지만, 메모리 효율면에서 매우 비효율적이며, 실행 시간이 매우 오래걸린다(시간복잡도가 높음)는 확실한 단점이 존재한다. 따라서 가능한 경우의 수가 적을 때만 사용하는 것이 바람직하며, 경우의 수가 커지면 실행 시간이 급격하게 늘어나므로 다른 효율적인 알고리즘으로 대체해야 한다.

대표적으로 크게 두 가지 상황에서 사용한다.

• 프로세스 속도를 높이는데 사용할 수 있는 다른 알고리즘이 없는 경우
• 문제를 해결하는 여러 솔루션이 있고, 각 솔루션을 확인해야 하는 경우

이처럼 문제에 더 적절한 해결 방법을 찾기 전에 시도해보는 알고리즘이라고 할 수 있다.

구현 방법

1. 반복문 활용

대표적인 방식으로, 그저 for문을 여러번 중첩해서 구현시키는 방식이다. 보통 이중 for문까지는 주로 많이 쓰지만, 그 이상으로는 잘 중첩시키지 않는데, 이 알고리즘에서는 필요할 수도 있다. 그냥 딴거 쓰면 안ㄷ

import java.io.*;
import java.util.StringTokenizer;

public class Main {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
        StringTokenizer st = new StringTokenizer(br.readLine());

        int N = Integer.parseInt(st.nextToken());
        int M = Integer.parseInt(st.nextToken());

        int [] numberArray = new int[N];

        st = new StringTokenizer(br.readLine());
        br.close();

        for(int i = 0; i < N; i++) {
            numberArray[i] = Integer.parseInt(st.nextToken());
        }
        bw.write( blackjack(numberArray, N, M) + "\n");
        bw.flush();
        bw.close();

    }

    public static int blackjack(int[] arrays, int N, int M){
        int sum = 0; //3수의 합을 구하는 변수
        int temp = 0; //근사치를 저장하여 저장하는 변수 (이전 for문의 3개의 합을 더해서 계속 비교해준다.

        for(int i = 0; i < N-2; i++) { //숫자가 겹치면 안되기 때문에 i는 0부터 시작하고 N-2까지
            for(int j = i+1; j < N-1; j++) { // 다음 j는 i+1 부터 시작하고 N-1까지
                for(int k = j+1; k < N; k++) { //다음 k는 j+1부터 시작 N까지 반복
                    sum = arrays[i] + arrays[j] + arrays[k]; //3수를 합쳐서
                    if(sum == M){ //수가 이미 같으면 바로 return 한다.
                        return sum;
                    }
                    if(sum > temp && sum <= M){ //이전 근사치보다 큰데 M보다 작거나 같다는 것은 이전 근사치보다 M에 가깝다는 뜻
                        temp = sum;
                    }
                }
            }
        }
        return temp; // 완전히 같은 수가 없을 때는 temp(가장 근사치)반환
    }
}

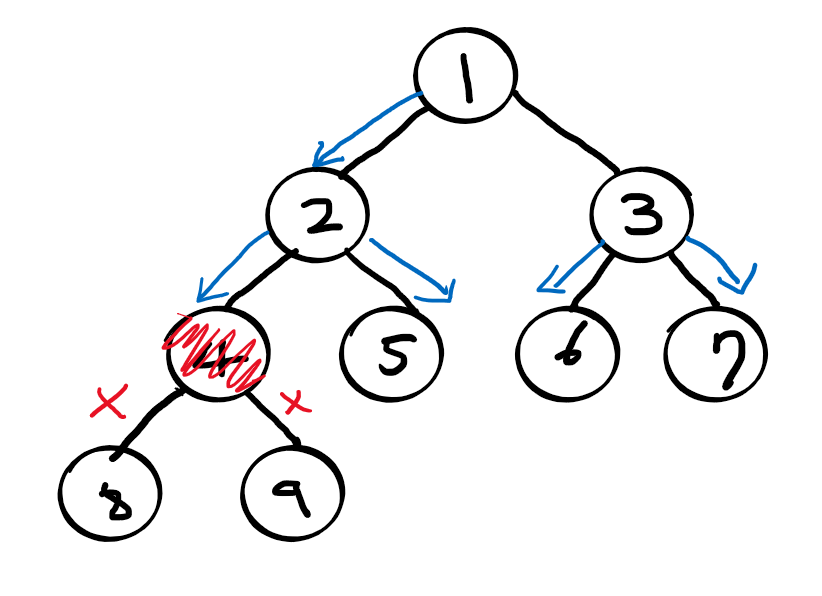
2. 재귀(백트래킹)

동일한 코드를 반복하는 반복문을 피하고자, 재귀를 활용하여 조금 더 코드를 간단하게 구현할 수 있다. base case(기저 조건)을 잘 설정한 후에, 반복문의 중첩을 재귀로 풀어내는 방식이다.