Cominciamo!
대단원의 마지막. 데이터 구조 힘들었다. 그치만 잘했다. 고생했다.
1. Graph, 그래프
1-1. 그래프란?
정점(vertex/Node)와 간선(edge)로 이루어진 자료 구조
정점간의 관계를 보여준다. 그래프에서는 정점간의 간선이 없을 수도 있고, 한 방향 혹은 양방향으로 방향성을 가지며, 이 방향성에 가중치를 줄 수도 있으며, 트리가 부모-자식간의 종속적인 관계를 가진다면 그래프는 순환/비순환의 관계를 보여준다.
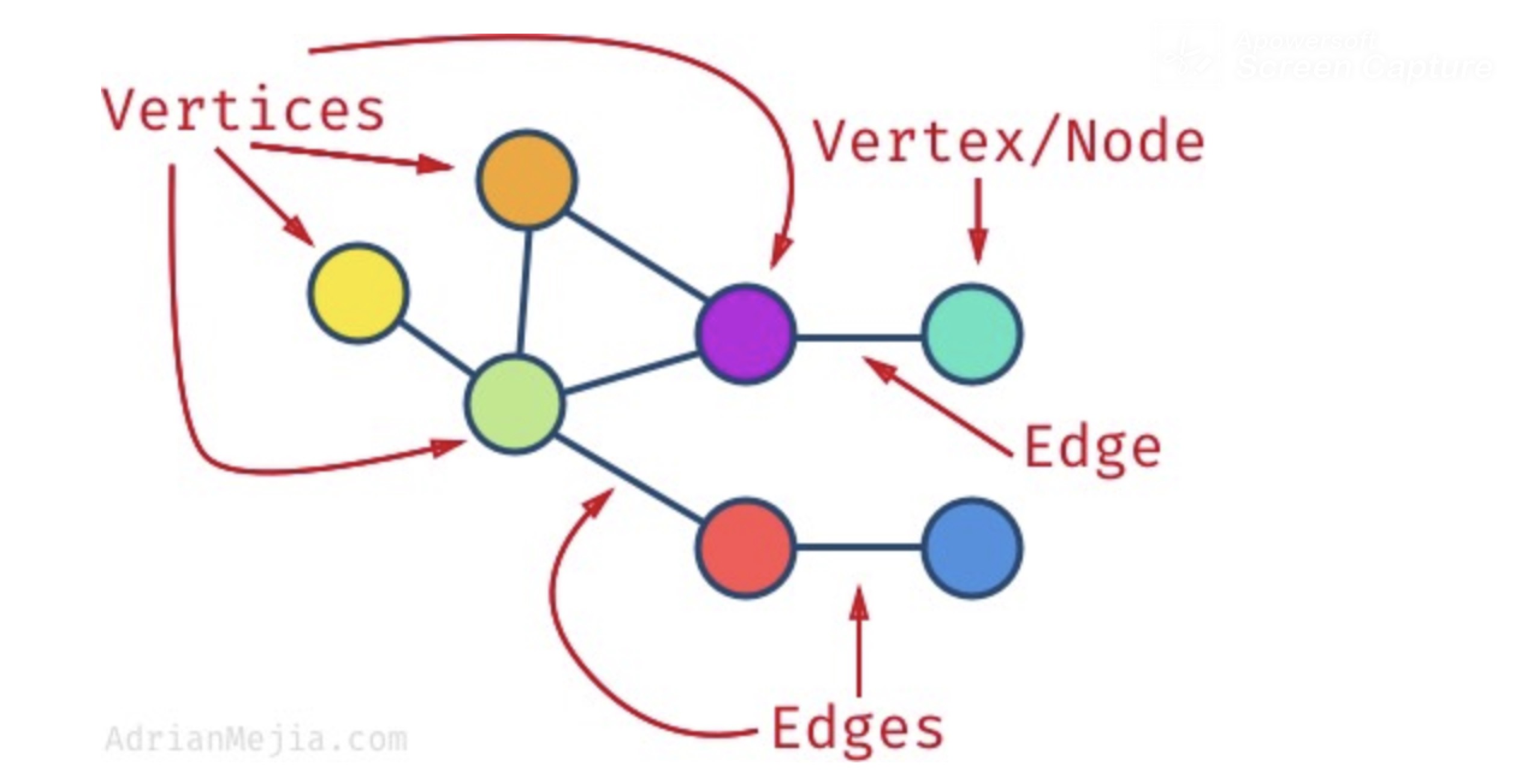
출처 및 참고자료 : Dylan North의 비기너를 위한 데이터 스트럭쳐
1-2. 그래프의 종류
- undirected graph : 간선(edge)에 방향성이 없는 그래프. 보통 양방향일 때, 이렇게 간선에 방향이 없다.

- directed graph : 간선(edge)가 방향성을 가지는 그래프. 기본적으로 방향성을 가질 땐 일방통행이라고 생각하면 된다. 그래서 한방향으로만 이동가능함.
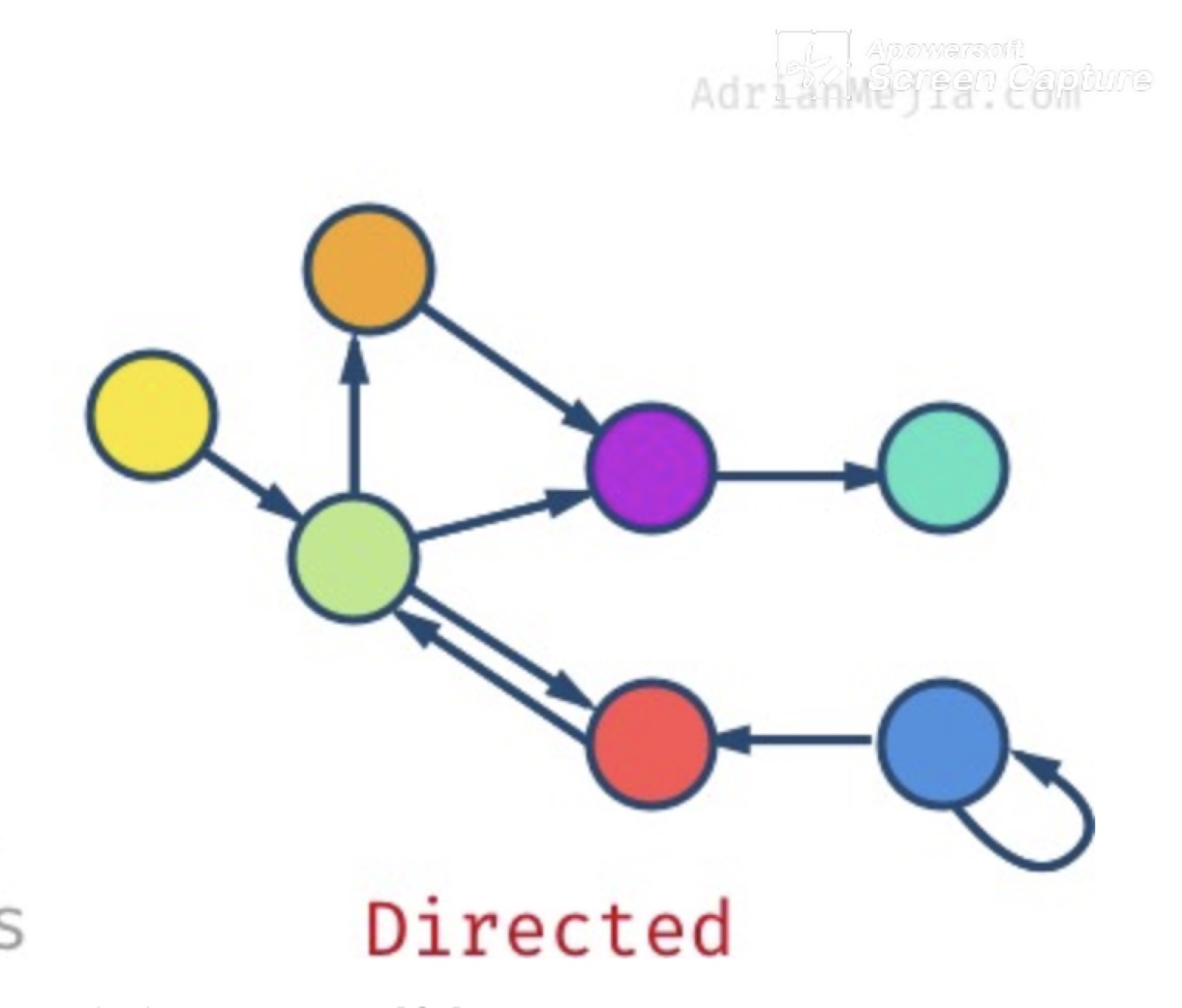
- self loop : 위 그림에서처럼 파란색 정점은 자신에게 방향을 가지고 있다. 이런 경우를 셀프 루프라고 한다.
1-3. 그래프의 실사용 예제
- 텔레콤의 송수신탑(기지국)
- 네비게이션(차량, 비행기)
- 소셜 네트워크
- 그리고 찾다보니, <Recommendations: Amazon/Netflix uses graphs to make suggestions for products/movies> 이런 항목도 있다. 아마존/넷플의 상품추천도 그래프로 진행한다고. 신기....
1-4. 그래프 구현
이런 그래프를 구현할 때는 매번 실제로 저렇게 그릴 순 없으니까... 몇 가지 다른 방법을 사용하는데, 인접리스트와 인접행렬이 그것이다.
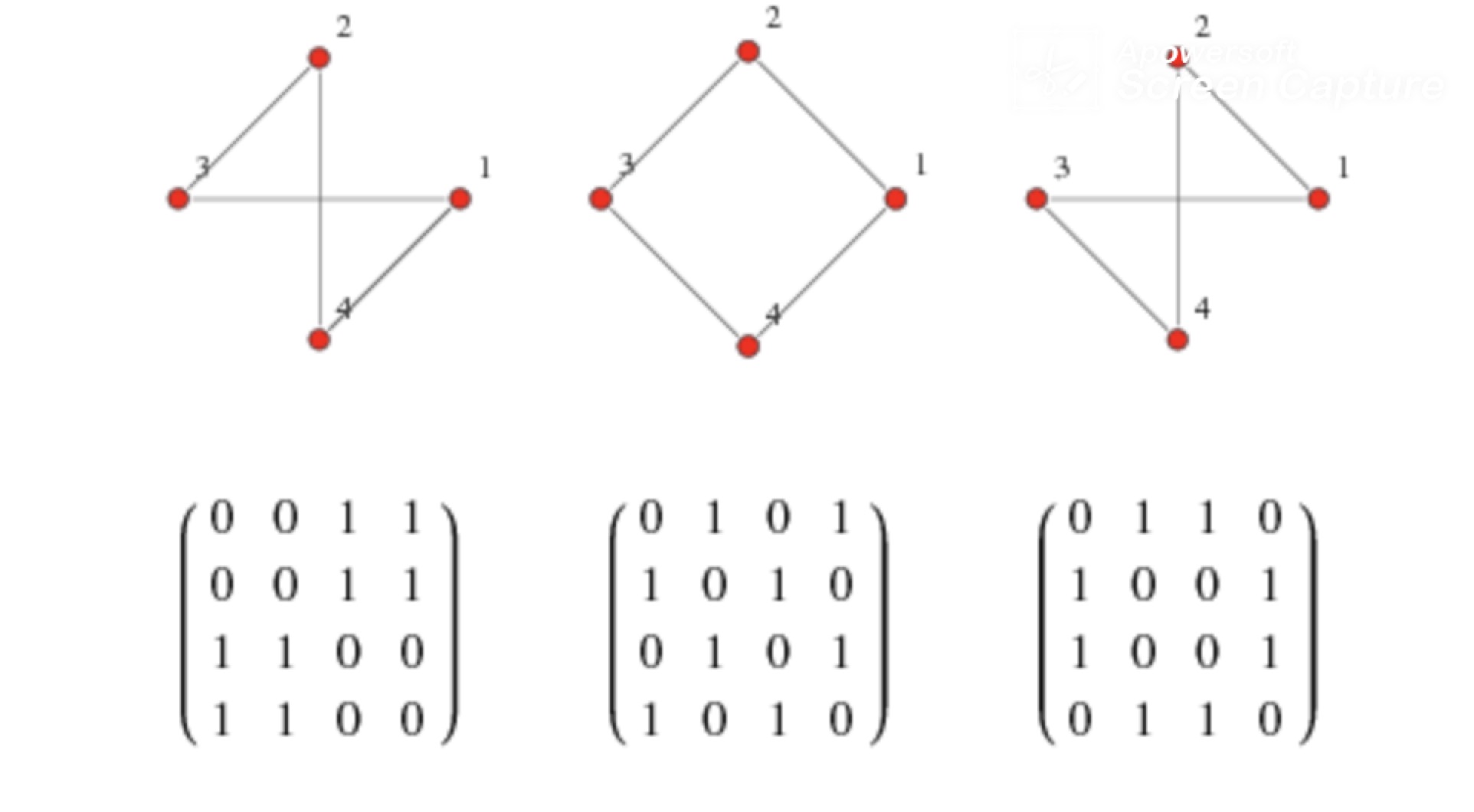
- 인접 행렬 : 인접행렬은 위와 같이 NxN매트릭스(행렬)을 사용해서 표현하는 방법이다. (방향성이 없는 그래프 같은 경우는 인접행렬로 표현하면 대칭성이 두드러진다, 물론 항상 그런 것은 아님 !!!!!).
-
인접행렬에서의 시간복잡도는 정점을 추가/삭제할 때는 행과 열에 모두 추가해줘야 하기 때문에 정점/노드의 갯수의 제곱만큼 시간이 필요함. 따라서 O(n^2). 그러나 간선의 경우는 특정 셀의 값만 삭제하거나 추가하면 되기 때문에 O(1)의 시간 복잡도를 가짐.
-
단점 : 연결된 노드나 간선의 갯수에 상관 없이 무조건 NxN개의 공간을 써야함.
-
장점 : 노드간의 연결 여부는 O(1)으로 알 수 있음.
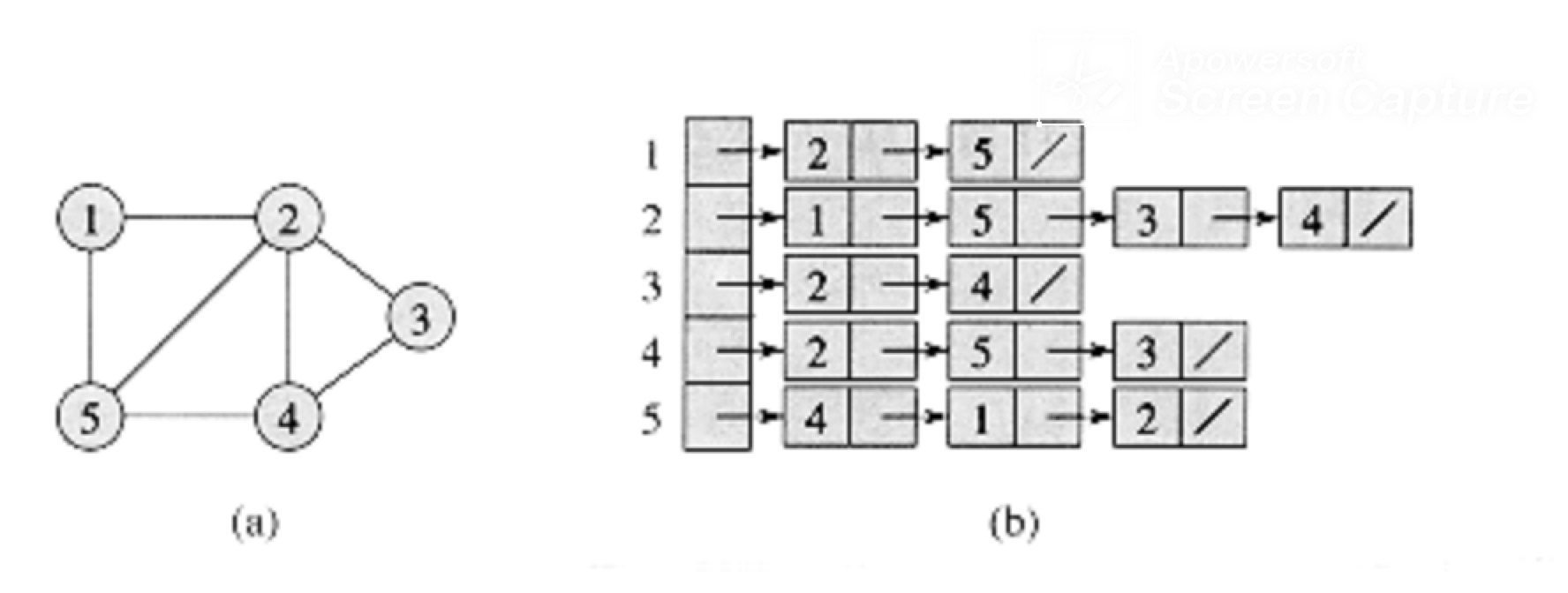
- 인접 리스트 : 위와 같이 링크드 리스트를 이용해서 구현한다.
- 인접리스트에서의 시간복잡도는 간선과 정점을 추가할 때는 tail의 nextNode로 지정하면 되기 때문에 O(1)이며, 정점을 삭제 할 때는 삭제된 자리에 새로운 값을 연결해 넣어야 하기 때문에 간선과 정점을 모두 다시 찾아야함. 그래서 시간복잡도는 O(V+E)이다. 간선을 삭제 할 때도 마찬가지다. 최악의 경우에는 1줄의 링크드 리스트라서, 찾을 때까지 계속 탐색을 해야 할 수도 있기 떄문에 O(E)의 시간복잡도를 가진다.
1-5. 그래프 탐색
#1. 깊이우선탐색, Depth First Search (스택/재귀함수 사용)
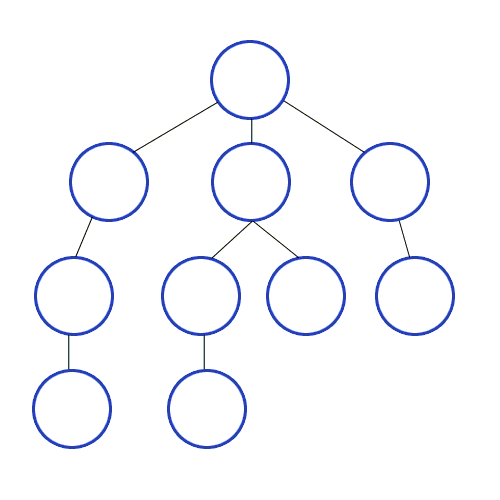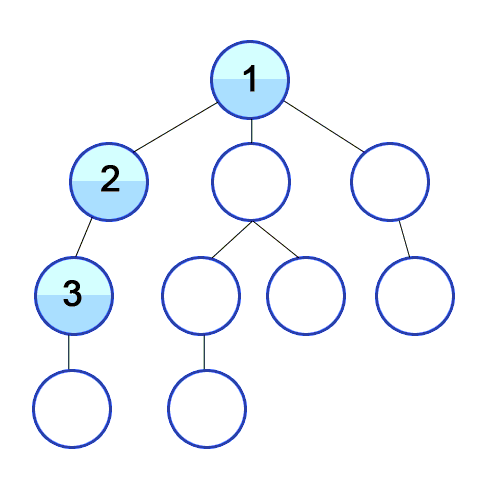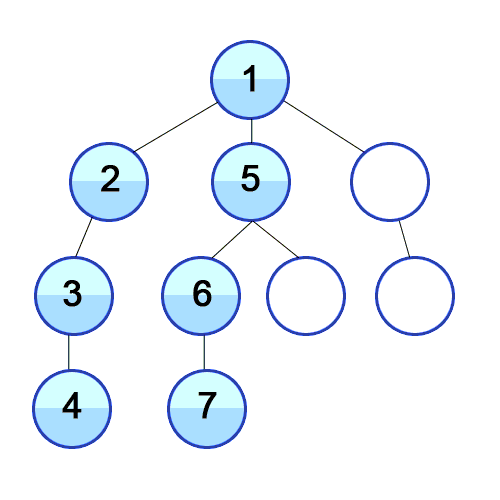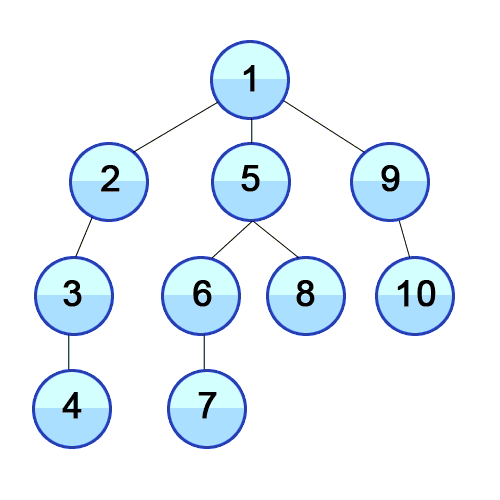
깊이 우선탐색은 위 그림과 같이 어떤 한 depth를 먼저 탐색하고, 더 이상 갈 곳이 없으면 가장 마지막 간선이 있는 갈림길로 돌아와 다시 다른 방향의 간선을 탐색하는 방식. 모든 정점을 탐색해야 할 떄 유리한 방식.
#2. 넓이우선탐색, Breath Frist Search (큐 사용)
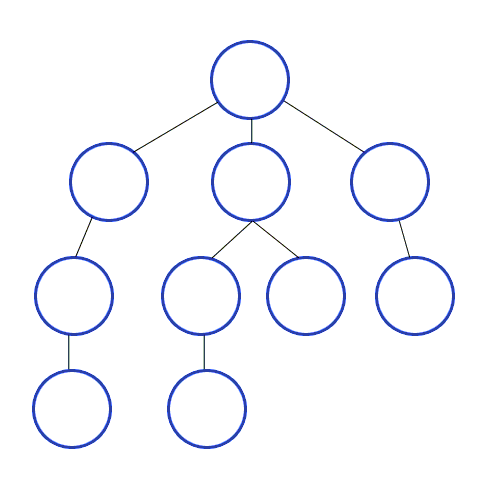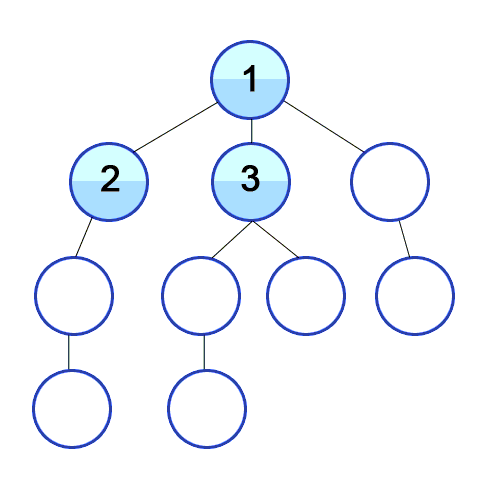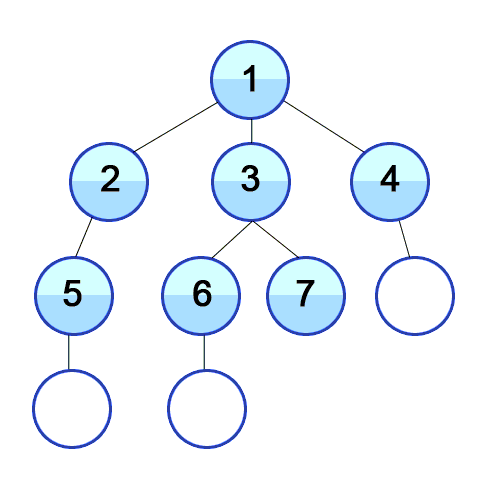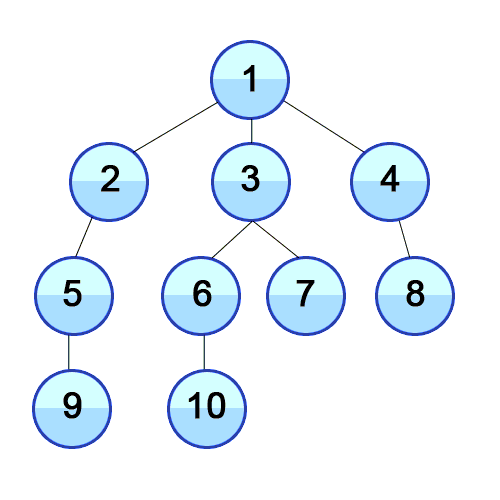
넓이우선탐색은 시작 정점을 기준으로 인접한 정점을 모두 탐색하고, 멀리 떨어진 정점을 나중에 탐색하는 방식. 두 노드 간의 최단 거리를 찾고 싶을 때 이용하기 좋은 방식.
2. Tree, 트리
(트리 아니죠.. 츄리.... 지나가세요... )
2-1. 트리란?
그래프의 일종으로, 부모-자식간의 관계를 가지는 자료구조를 의미한다.
트리는 보통 방향성을 가진 비순환구조의 그래프라고 간주한다. 그렇기 때문에 self loop은 존재하지 않는다.
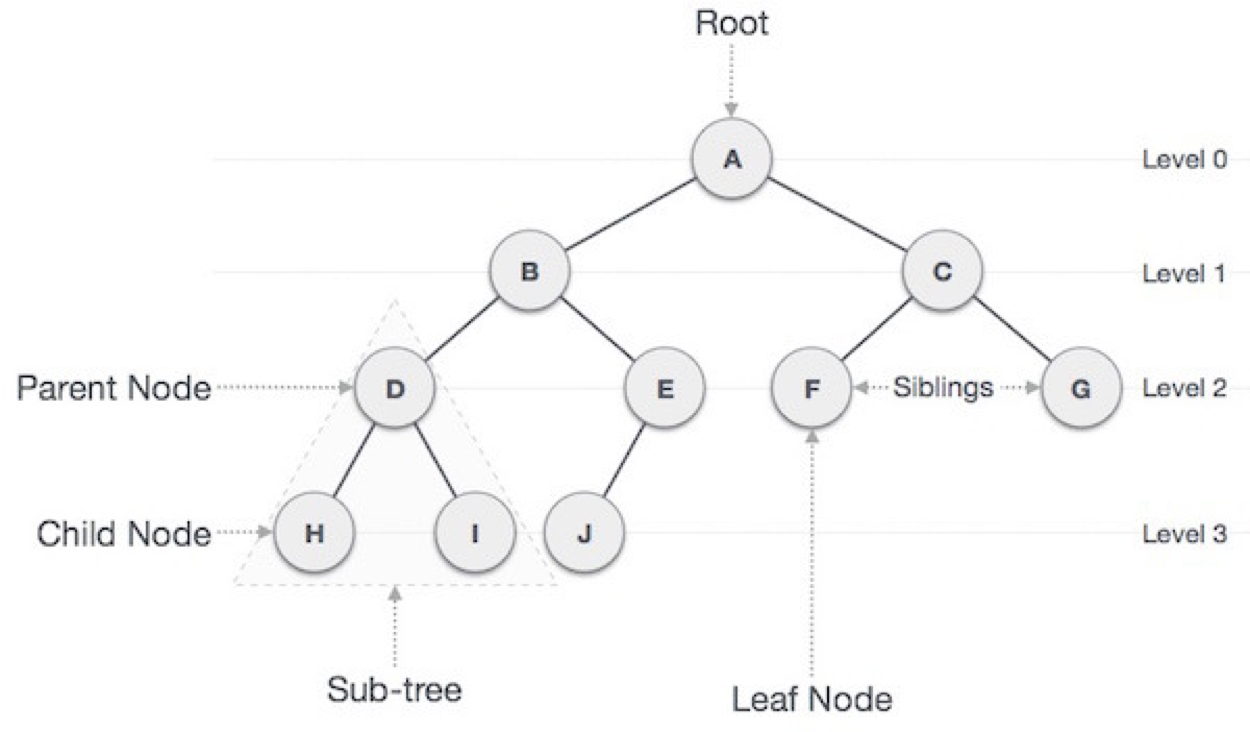
위 그림의 출처는 여기. 참고.
(아.. 여기까지 썼는데 그래프에서 너무 힘줘서... 이제 쓰기 싫... 네 마음의 소리니까 지나가세요 )
2-2. 트리의 종류
출처 및 참고자료. 여기에 트리 종류 구분 & 다이어그램이 예쁘게 되어 있음...캬캬

- 이진트리 : 모든 트리가 이진트리는 아니다. 하나의 부모노드가 1~2개의 자식노드를 가지는 트리.
<이진트리의 종류는 영어로 알아두는게 편할 것 같아서, 영어로만 기재>
- Full Binary Tree : 부모노드가 0개 혹은 2개의 자식노드르 가짐.
- Complete Binary Tree : 마지막 레벨의 노드들이 자식노드의 왼쪽부터 채워진 이진트리.
- Perfect Binary Tree : 모든 Leaf가 2개의 노드로 구성된 트리.
- 이진탐색트리 : 부모노드의 왼쪽 자식노드는 부모보다 작고, 오른쪽 자식노드는 부모보다 큰 값을 가진다.
2-3. 트리의 탐색
1) 전위순회(pre-order) :"부모 - 좌 - 우"
2) 중위순회(in-order) : "좌 - 부모 - 우"
3) 후위순회(post-order) : "좌 - 우 - 부모"
2-4. 트리 시간복잡도 참고자료
Finiamo!
데이터 구조, 어려웠지만 그래도 재밌었다. 앞으로도 화이팅.