1. 문제 소개

Constraints:

• 1 <= target.length <= 10^5
• 1 <= target[i] <= 10^5

1526. Minimum Number of Increments on Subarrays to Form a Target Array

2. 나의 풀이법

처음엔 어려움 난이도라 겁이 났는데, 코드를 하나하나 살펴보니 규칙이 보였다.
핵심은 이전보다 이후가 얼마나 커졌는지만 더해주면 된다는 점이었다.
subarray가 새로 시작되는 시점이 바로 이전 값보다 이후 값이 더 커질 때이기 때문이다.
이 풀이는 길이 n에 비례해 시간복잡도가 $O(n)$이다.

class Solution:
    def minNumberOperations(self, target: List[int]) -> int:
        n = len(target)
        ans = target[0]

        for i in range(n-1):
            prev, nxt = target[i], target[i+1]
            if prev < nxt:
                ans += nxt - prev
        return ans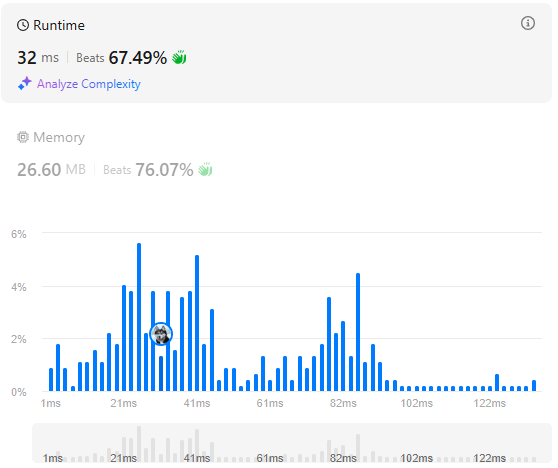

3. 다른 풀이법

한 줄 짜리 코드가 있어 가져왔다.
똑같이 시간복잡도는 $O(n)$이지만 나의 경우는 if문으로 연산을 하지 않고 넘어간 부분이 있는 반면, 다른 풀이의 경우 max() 함수를 사용해 연산량이 증가해 살짝 느려졌다.

class Solution:
    def minNumberOperations(self, target: List[int]) -> int:
        return target[0] + sum(max(0, b - a) for a, b in zip(target, target[1:]))

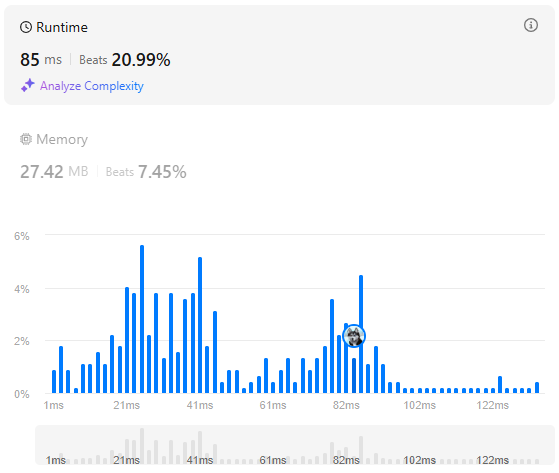
4. 결론

규칙만 잘 살펴본다면 어려운 문제도 어렵지 않다.