Leetcode
1.leetcode-2221. Find Triangular Sum of an Array

처음 이 문제를 보았을 때에 각각의 항이 몇 번 반복적으로 더해지는 지를 알 수 있다면 $O(n^2)$까지는 걸리지 않을 것이라고 생각했다.실제로 이항계수와 관련이 있었고 그렇게 푼 풀이도 맞았다.그러나 이 풀이법은 시간 복잡도는 $O(n)$이지만 math 라이브러리
2.leetcode-1518. Water Bottles
1. 문제 소개 1518. Water Bottles 2. 나의 풀이법 파이썬의 divmod()를 사용하면 몫과 나머지를 쉽게 구할 수 있다. 다음과 같이 풀어보았다. 결과는 생각보다 안
3.leetcode-3100. Water Bottles II
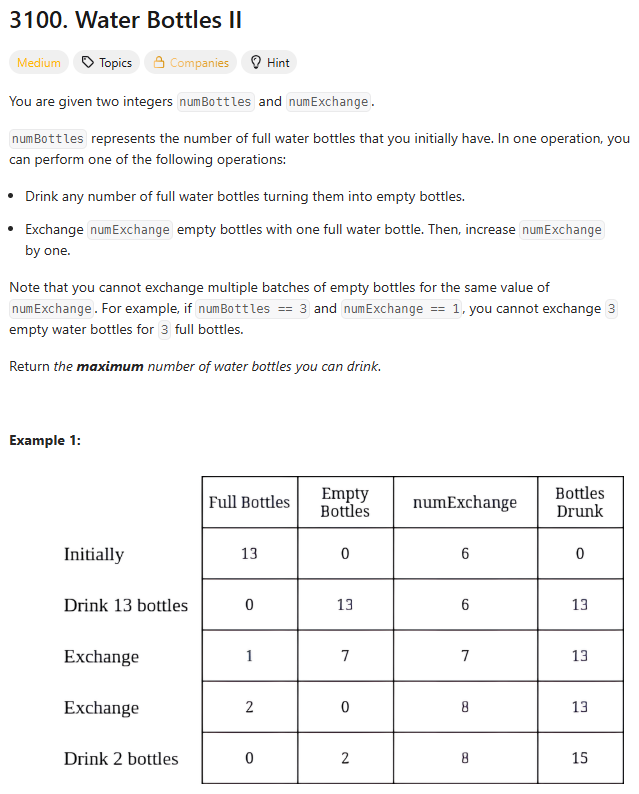
3100\. Water Bottles II어제와 비슷하지만, 교환에 필요한 빈 병이 계속 늘어나는 차이점이 존재한다.한 번에 좋은 성적을 거두었다.내 풀이의 시간복잡도는 $O(n)$정도라고 할 수 있다.내 풀이와 비슷하지만 조금 다르다.나는 매 루프마다 교환을 1번씩
4.leetcode-407. Trapping Rain Water II
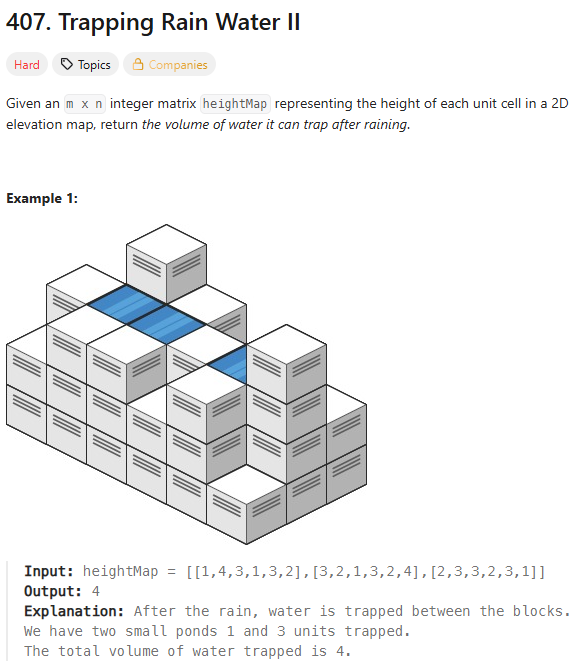
407\. Trapping Rain Water II길이 $n$의 리스트로 풀었을 때에는 투포인터 방식으로 풀었기에, 이것도 비슷한 것인 줄 알았는데, BFS와 Heap으로 푸는 것이라고 한다.감이 잘 안잡혀서 조금 찾아보며 풀었다.다른 풀이법과 나의 풀이법은 거의 똑같
5.leetcode-11. Container With Most Water
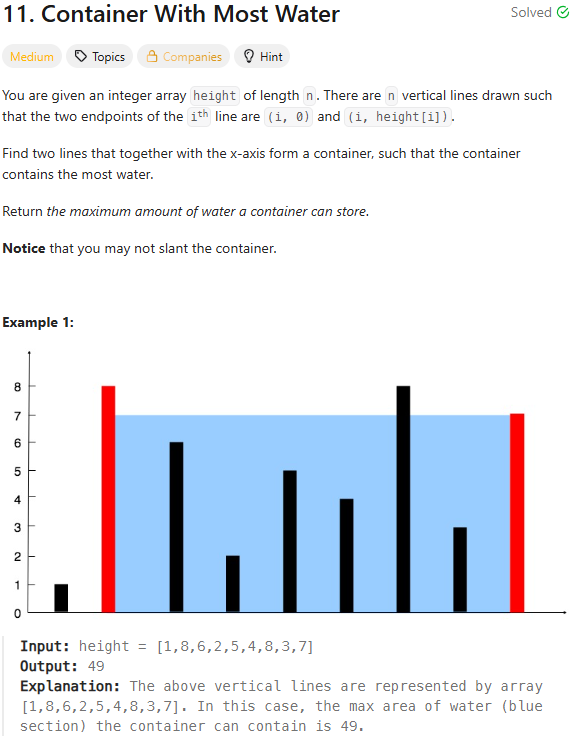
11\. Container With Most Water이번에는 투 포인터 방식으로 풀었다.높이와 길이만 따져서 풀면 되는 방식이다.다른 풀이법도 방향성은 같지만, max()가 아니라 if문으로 분기처리를 사용하는 것이 훨씬 빠른 풀이를 보장하는 것으로 보인다.모두 시간
6.leetcode-417. Pacific Atlantic Water Flow

leetcode-417. Pacific Atlantic Water Flow어제 풀었던 407. Trapping Rain Water II의 방식과 비슷하게 풀었다. 분수령을 찾기 위해서 바다를 맞는 경계면부터 더 이상 올라갈 수 없는 곳까지 올라가는 방식으로 풀어보았다.
7.leetcode-778. Swim in Rising Water

778\. Swim in Rising Water보자마자 bfs가 떠올랐다. 문제는 $t$에 따라서 어떻게 효율적으로 알고리즘을 조정하는 것이다. 감이 잘 안잡혀 조금 검색하며 풀어보았다.꽤나 좋은 성적을 냈다.이전 문제와 비슷하게 풀었는데 말이다.기분이 좋다.이 경우
8.leetcode-1488. Avoid Flood in The City

1. 문제 소개 1488. Avoid Flood in The City 2. 나의 풀이법 문제는 홍수가 나지 않도록 호수에 두 번 이상 비가 내리지 않도록 조절하는 것이다. 비가 두 번 오기 전, 어떤 순서로 호수에 고인 물을 빼내는 방법을 고민하는 것이 관건이다.
9.leetcode-3346. Maximum Frequency of an Element After Performing Operations I

3346\. Maximum Frequency of an Element After Performing Operations I문제를 처음 보았을 때에는 어떻게 푸는지 감이 잘 잡히지 않았다.그래서 문제의 Editorial과 Solutions의 힌트를 살펴보며 풀었다.아래의
10.leetcode-3461. Check If Digits Are Equal in String After Operations I

3461\. Check If Digits Are Equal in String After Operations IEasy난이도 문제였기에 쉬웠다.간단한 반복문을 사용해서 문제를 풀었다.그러나 각 단계별로 반복문을 사용해 시간복잡도가 $O(n^2)$이어서 느리게 풀리는 것
11.leetcode-2048. Next Greater Numerically Balanced Number

2048\. Next Greater Numerically Balanced Number처음 생각은 dfs였다.문제의 범위는 $10^6$까지였고, 그에 맞춰서 상한을 정해두었다.이후에는 list에 숫자의 사용횟수를 적어가며 계산했다.Editorial의 풀이는 굉장히 단순한
12.leetcode-3354. Make Array Elements Equal to Zero

3354\. Make Array Elements Equal to ZeroEasy난이도라 간단한 풀이였다.값이 0인 인덱스를 고르고 그 인덱스를 기준으로 왼쪽합과 오른쪽합이 같은지, 차이가 1인지, 마지막으로 다른 지에 대해서 알아보면 되었다.하지만 첫 풀이는 반복적으로
13.leetcode-1716. Calculate Money in Leetcode Bank
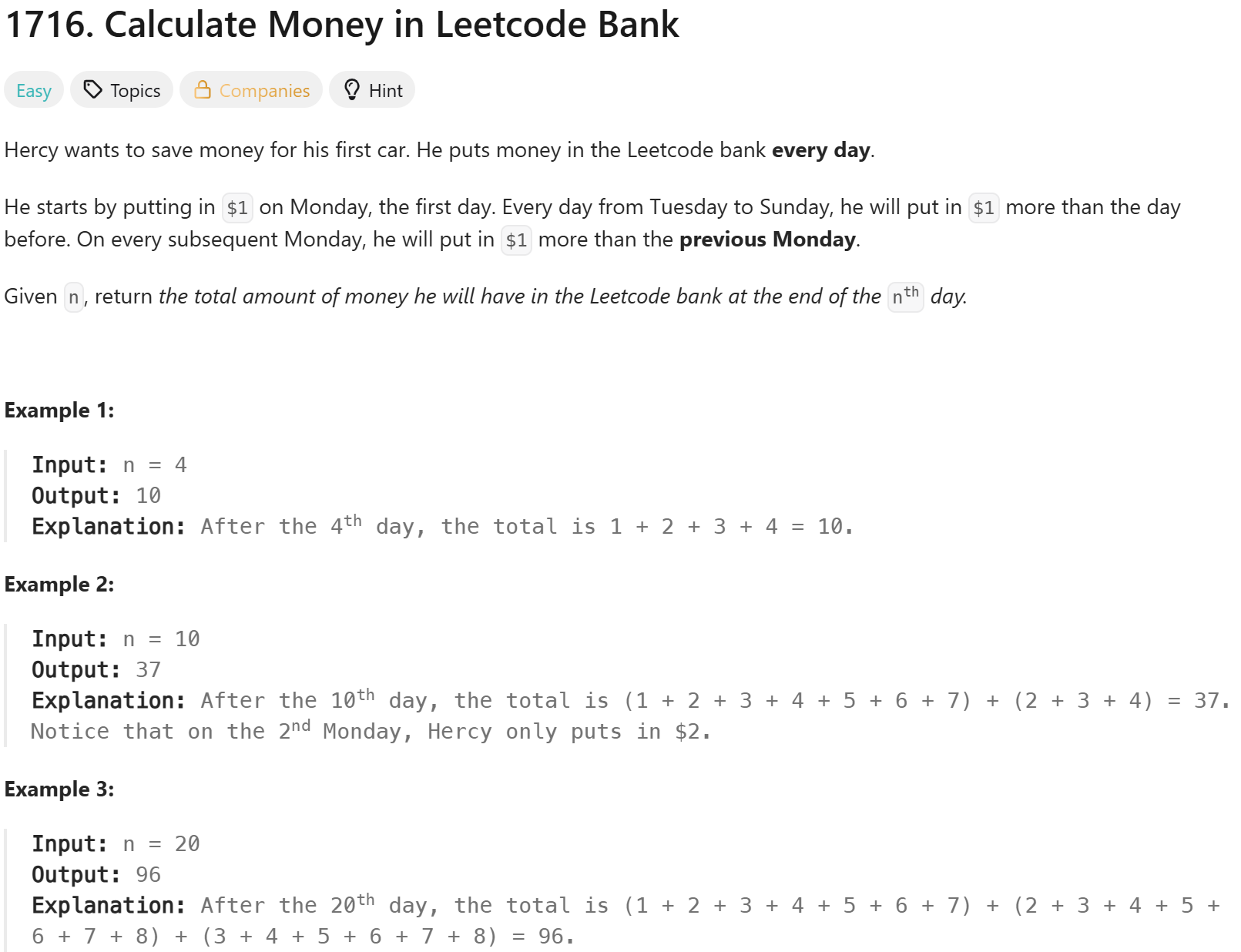
Constraints:1 <= n <= 10001716\. Calculate Money in Leetcode Bankdivmod()를 사용해 몫q과 나머지r를 구하고, 이에 맞춰서 셈을 했다.시간 복잡도는 $O(q)$이다.물론 아래처럼 공식을 전부 사용해
14.leetcode-2043. Simple Bank System

2043\. Simple Bank System문제의 설명 그대로 간단하게 구현만 하면 되는 문제였다.어렵지는 않았으나, 효율적인 풀이가 무엇인지 조금 고민이 되었다.각 연산의 시간복잡도는 $O(1)$이고 공간복잡도는 $O(n)$이다.다른 풀이법도 나와 별 다를 것이 없
15.leetcode-2125. Number of Laser Beams in a Bank

2125\. Number of Laser Beams in a Bank각 행마다 1이 몇개씩 있는지를 세고, 이전과 이후 행의 곱을 차례로 더하는 방식으로 코드를 짰다.이 경우에는 시간복잡도는 $O(mn)$이다. 문제 풀이의 방식은 같지만 코드는 더 효율적이다이 경우도
16.leetcode-3370. Smallest Number With All Set Bits
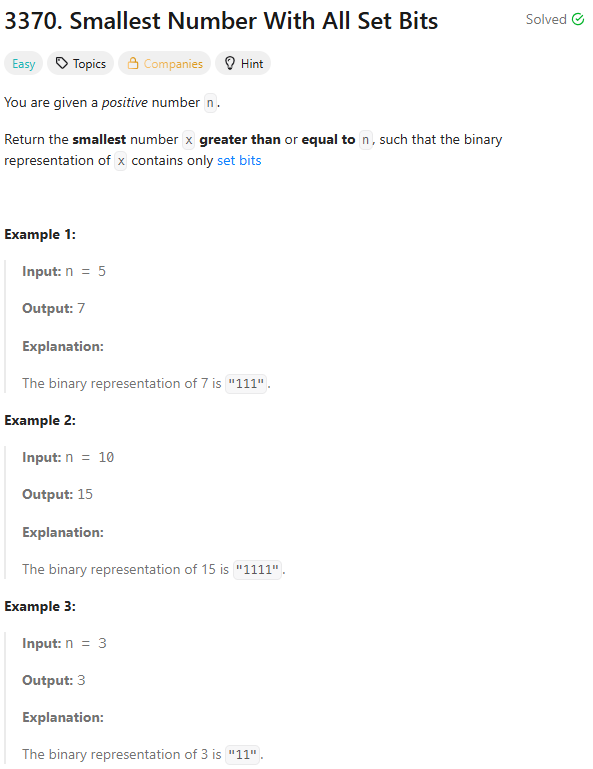
Constraints:1 <= n <= 10003370\. Smallest Number With All Set Bits간단하게 bin()함수를 사용해 이진화했고 그 길이만큼의 1로 이루어진 비트를 다시 정수화했다.아쉬운 점은 이미 조건을 만족하는 n에 대해서
17.leetcode-1526. Minimum Number of Increments on Subarrays to Form a Target Array

Constraints:1 <= target.length <= 10^51 <= target\[i] <= 10^51526\. Minimum Number of Increments on Subarrays to Form a Target Array처음엔 어려
18.leetcode-3289. The Two Sneaky Numbers of Digitville

3289\. The Two Sneaky Numbers of Digitvillenums의 모든 숫자를 순회하여 두 번 나타나는 숫자만 골랐다.시간복잡도는 $O(n)$이다.이렇게 collections.Counter를 사용하면 한 줄로도 풀 수 있다.반복문을 두 번 돌리는
19.leetcode-3217. Delete Nodes From Linked List Present in Array

3217\. Delete Nodes From Linked List Present in Arrayhead.val이 nums안에 들어가면 다음 값으로 바꾸는 방식으로 풀었다.처음에는 if구문에서 리스트로 체크했을 때에는 시간초과가 되었지만, set으로 바꿔서 검사하니 시간
20.leetcode-2257. Count Unguarded Cells in the Grid

2257\. Count Unguarded Cells in the Grid처음에는 guard의 시선을 하나하나 생각한 계산을 사용했다.시간복잡도는 처음 그리드를 생성한 시간과 guard별로 한 번 순회를 반복해 $O(mn + |guards|·(m+n))$인데, m과 n의
21.leetcode-1578. Minimum Time to Make Rope Colorful

Constraints:n == colors.length == neededTime.length1 <= n <= 1051 <= neededTime\[i] <= 104colors contains only lowercase English letters.1
22.leetcode-

3318\. Find X-Sum of All K-Long Subarrays I문제의 설명대로 길이 k의 부분수열에서 빈도수를 계산하고 자주 등장한 숫자들로 x_sum을 답에 넣었다.슬라이딩 윈도우를 사용한 다른 풀이법도 존재한다.다양한 접근법이 존재하는 문제였다.
23.leetcode-3607. Power Grid Maintenance

3607\. Power Grid Maintenance잘 모르겠어서 답지를 보며 풀었다.heap을 사용한 풀이도 존재한다.요즘은 문제가 어렵다...
24.leetcode-2528. Maximize the Minimum Powered City

2528\. Maximize the Minimum Powered City풀지 못했다...접근법은 이분탐색(Binary Search)과 차분 배열(Difference Array), 그리디 전략(Greedy strategy)을 사용한 풀이이다. 이분 탐색(Binary Se
25.leetcode-1611. Minimum One Bit Operations to Make Integers Zero

1611\. Minimum One Bit Operations to Make Integers Zero처음 문제를 보았을 때에 발견한 규칙은 다음과 같았다.| input | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |\| --- \| --- \| --- \|
26.leetcode-2169. Count Operations to Obtain Zero

2169\. Count Operations to Obtain Zero간단하게는 문제의 규칙대로 큰 수에서 작은 수를 빼면 된다.그러나 조금 더 간단하게 풀고 싶어 생각을 해봤다.이 경우는 유클리드 호제법을 사용하면 몫과 나머지를 구하고 최대공약수를 구하는 시점까지의 몫
27.leetcode-3542. Minimum Operations to Convert All Elements to Zero

Constraints:1 <= n == nums.length <= 1050 <= nums\[i] <= 1053542\. Minimum Operations to Convert All Elements to Zero풀이는 다음의 이미지를 참고하며 풀었다
28.leetcode-474. Ones and Zeroes

474\. Ones and Zeroes처음 보았을 때에는 바로 감을 잡지 못했다.Dynamic Programming을 사용하여 풀 수 있다는 힌트를 보고 고민을 해봤다.각각의 이진숫자에 대해서 0과 1을 dp에 저장해가며 풀었다.중요한 점은 dp를 채울 때에 역순으로
29.leetcode-2654. Minimum Number of Operations to Make All Array Elements Equal to 1

2654\. Minimum Number of Operations to Make All Array Elements Equal to 1처음 든 생각은 인접한 배열이 서로소가 나온다면 끝나는 풀이라고 생각했다.배열에 1이 존재한다면 1을 제외한 만큼, 아니라면 배열 전체를
30.leetcode-3228. Maximum Number of Operations to Move Ones to the End

3228\. Maximum Number of Operations to Move Ones to the End처음 생각한 풀이는 최대 연산을 구하는 것이라 1을 만날 때마다 1을 만난 횟수로 저장하고, 0을 만날 때 1을 만난 횟수를 결과에 저장하는 것으로 생각했다.거의
31.leetcode-2536. Increment Submatrices by One

2536\. Increment Submatrices by One처음에는 단순하게 더하기만 하면 된다고 생각했는데 이 경우 시간초과가 날 수 있다.따라서 차분 기록과 누적 합을 사용하기로 했다.시간복잡도는 $O(q + n^2)$이다.
32.leetcode-3234. Count the Number of Substrings With Dominant Ones
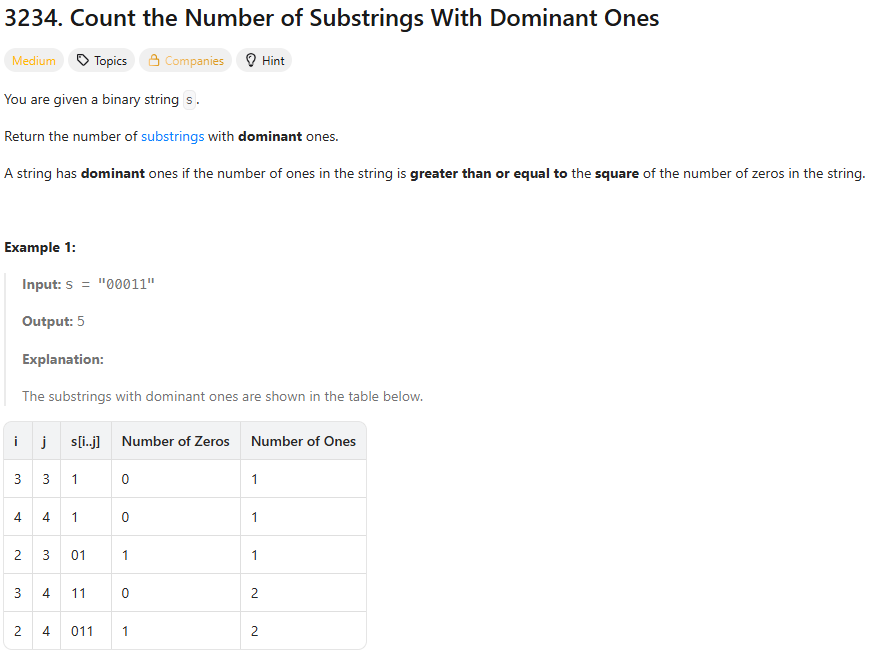
3234\. Count the Number of Substrings With Dominant Ones주말이라 그런지 혼자 힘으로 풀지 못했다.k=0 처리: 연속된 1 구간의 길이를 이용해, 0을 포함하지 않는 모든 부분문자열 수를 run-length로 바로 더한다.0
33.leetcode-1513. Number of Substrings With Only 1s

1513\. Number of Substrings With Only 1s문제의 힌트를 보고 어떻게 푸는 지 알았다.Count number of 1s in each consecutive-1 group. For a group with n consecutive 1s, the
34.leetcode-1437. Check If All 1's Are at Least Length K Places Away
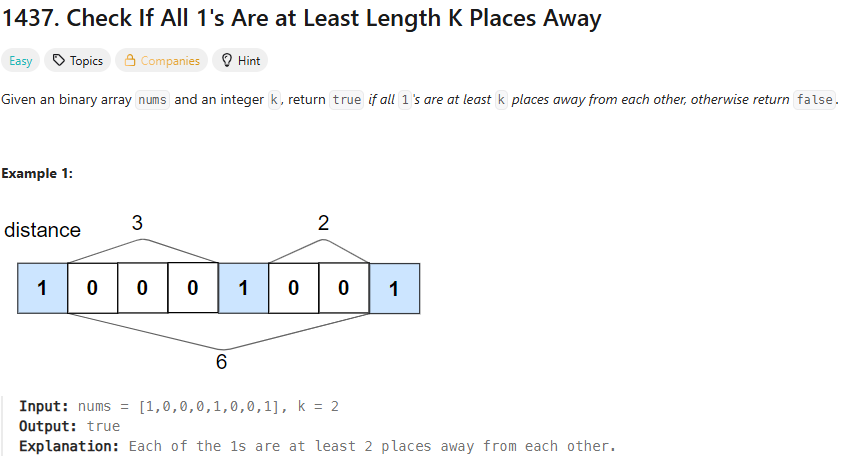
1437\. Check If All 1's Are at Least Length K Places Away처음 보자마자 nums를 순회하여 0을 만날 때마다 distance를 올렸고 1을 만날 때 d가 k보다 작은 경우 True/False를 체크했다.시간복잡도는 $O(n)
35.leetcode-717. 1-bit and 2-bit Characters

717\. 1-bit and 2-bit Characters처음봤을 때에는 문제를 잘 이해하지 못했는데, 알고보니 쉬운 문제였다.배열을 한 번 쭉 순회하며 되는 문제였다.시간복잡도는 $O(n)$이다.오늘도 내 힘으로 풀어서 좋다.
36.leetcode-2154. Keep Multiplying Found Values by Two
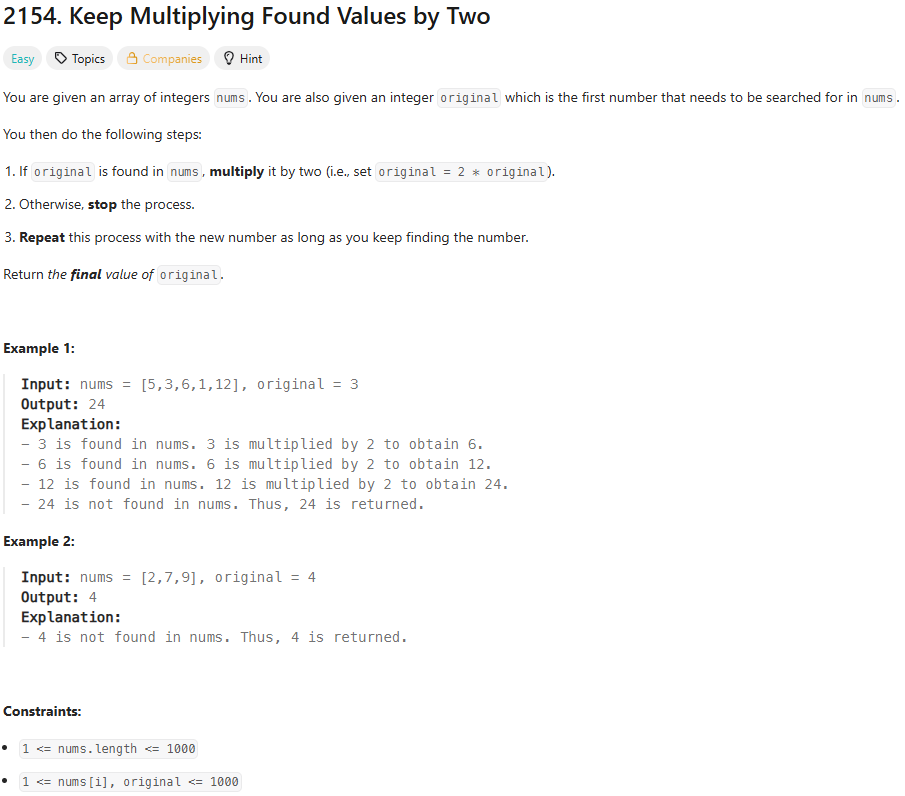
2154\. Keep Multiplying Found Values by Two풀이 자체는 쉬웠으나 빠르게 푸는 방법을 고민해야하는 문제였다.nums를 정렬하고 전체 배열을 한 번만 순회하는 방향으로 풀었고, 시간복잡도는 정렬로 인해 $O(n \\,log n)$이다.이렇
37.leetcode-757. Set Intersection Size At Least Two

Constraints:1 <= intervals.length <= 3000intervals\[i].length == 20 <= start_i < end_i <= 10^8757\. Set Intersection Size At Least Two처
38.leetcode-1930. Unique Length-3 Palindromic Subsequences
1. 문제 소개 1930. Unique Length-3 Palindromic Subsequences 2. 나의 풀이 3. 다른 풀이 4. 결론
39.leetcode-3190. Find Minimum Operations to Make All Elements Divisible by Three

3190\. Find Minimum Operations to Make All Elements Divisible by Three배열을 한 번 순회해 3으로 나눠지지 않는 숫자의 개수가 정답이다.시간복잡도는 $O(n)$이다.이번에는 진짜로 너무 쉬운 문제였다.
40.leetcode-1262. Greatest Sum Divisible by Three

1262\. Greatest Sum Divisible by Three나머지가 1일때 가장 작은 두 개의 숫자와 나머지가 2일때 가장 작은 두 개의 숫자, 총 4개의 숫자를 추적했다.총 합의 나머지가 1과 2일때를 나눠 최적의 숫자를 제거하는 방식으로 문제를 풀었다.시간
41.leetcode-1018. Binary Prefix Divisible By 5

1018\. Binary Prefix Divisible By 5배열을 순회하면서 이진수를 십진수로 변환하고 이를 5로 바꾼 나머지를 생각해 풀었다.
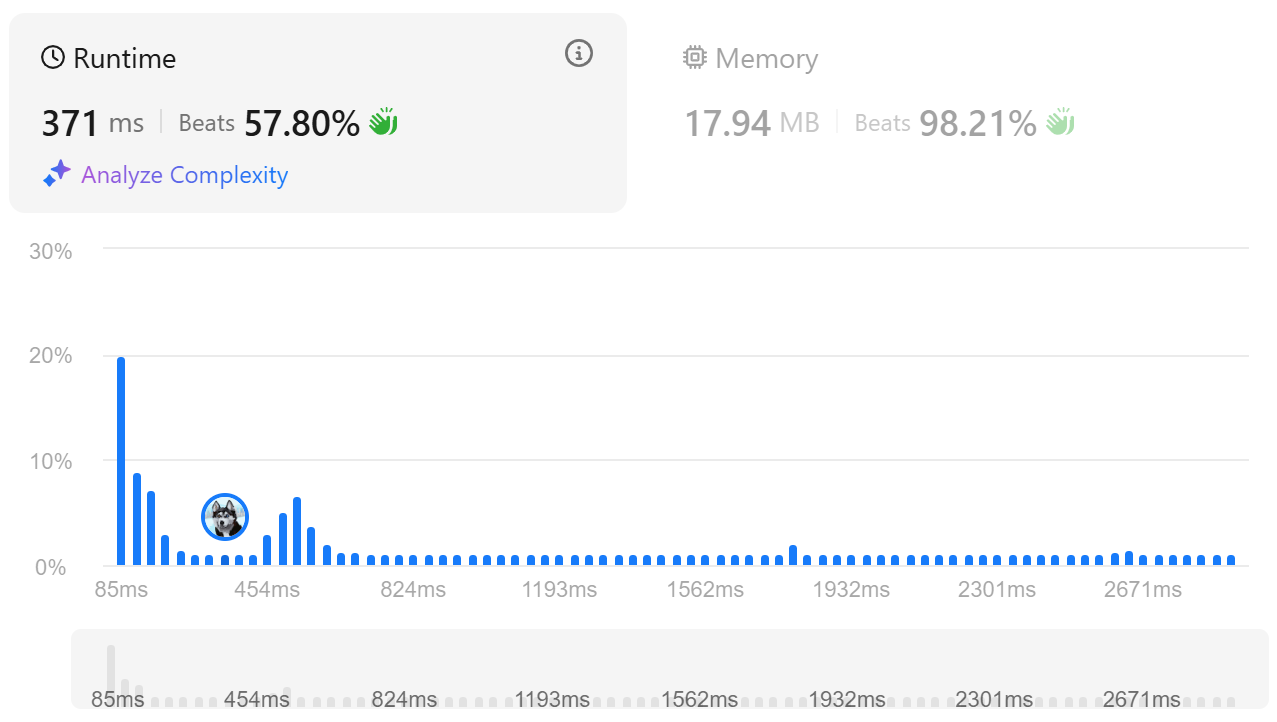
42.leetcode-1015. Smallest Integer Divisible by K
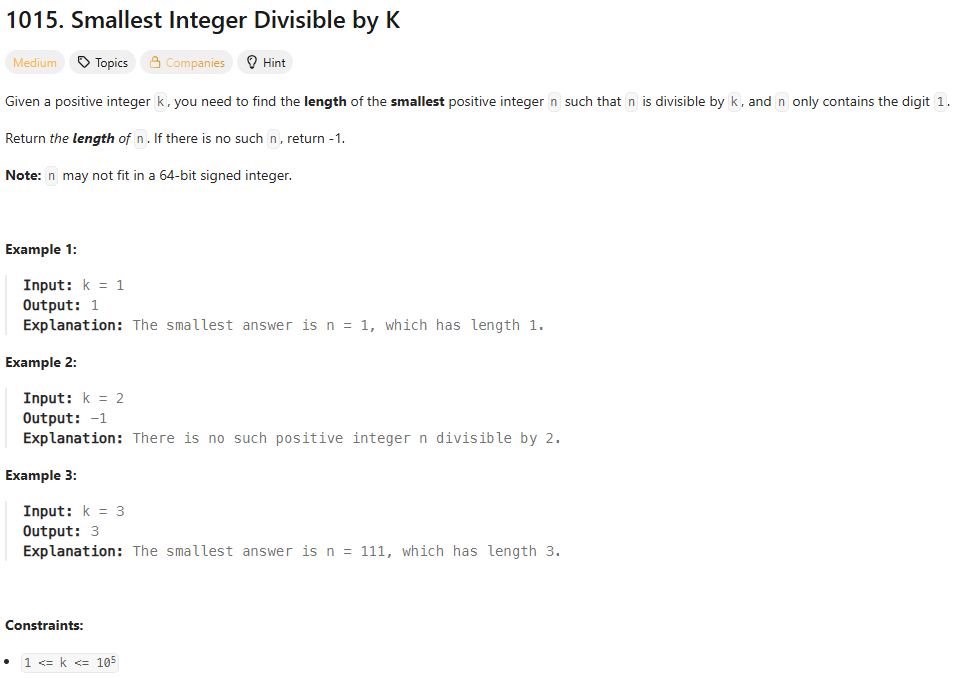
1015\. Smallest Integer Divisible by K간단하게 마지막 숫자가 1인 수를 나눌 수 없는 2와 5을 제외하고 modulo를 사용해서 풀었다.처음에는 ans %= k를 넣지 않아서 시간이 너무 늘었었는데, 추가하므로서 빠른 시간에 풀 수 있었다
43.leetcode-2435. Paths in Matrix Whose Sum Is Divisible by K

2435\. Paths in Matrix Whose Sum Is Divisible by K처음에는 dfs로 풀려고 시도했으나 dp가 맞는 방향이라는 힌트를 보고 방법을 바꿨다.단순하게 2차원 배열을 시도했지만 3차원 배열이 필요하다는 것을 깨닫고, 정답코드를 봐가며 풀
44.leetcode-3381. Maximum Subarray Sum With Length Divisible by K

Constraints:1 <= k <= nums.length <= 2 \* 105109 <= nums\[i] <= 1093381\. Maximum Subarray Sum With Length Divisible by K혼자 고민해봤을 때 pre
45.leetcode-3512. Minimum Operations to Make Array Sum Divisible by K

3512\. Minimum Operations to Make Array Sum Divisible by K모두 더하고 k로 나누었다.시간복잡도는 $O(n)$이다.
46.leetcode-1590. Make Sum Divisible by P
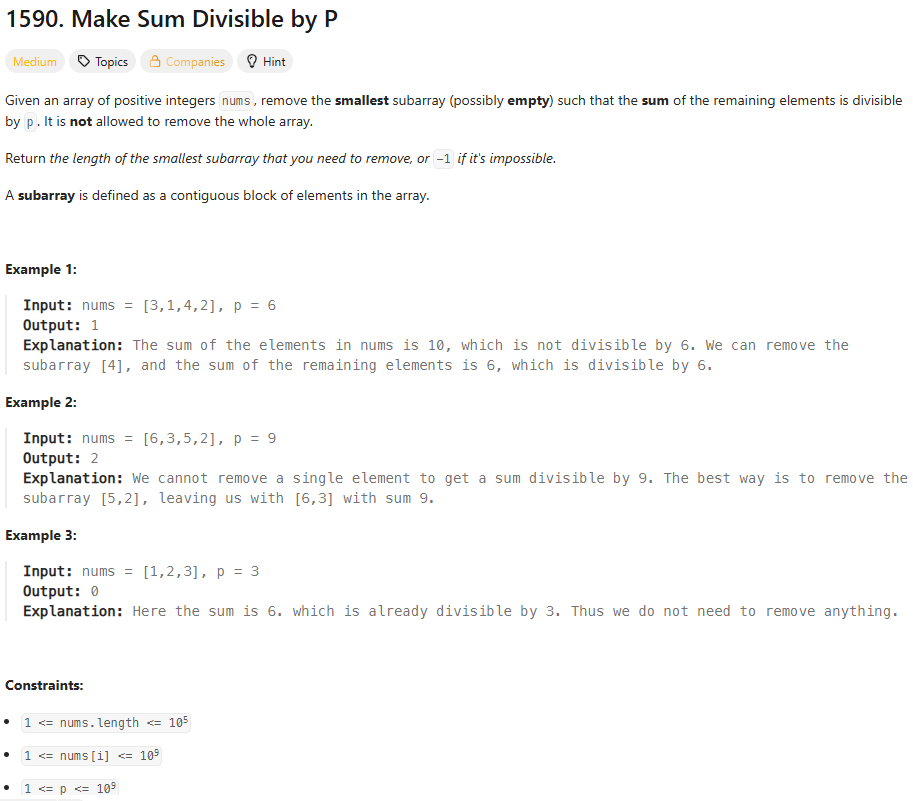
1590\. Make Sum Divisible by P오늘은 풀이가 잘 생각나지 않아 Editorial을 참고했다.시간복잡도는 $O(n)$이다.
47.leetcode-2141. Maximum Running Time of N Computers

2141\. Maximum Running Time of N Computers이진 탐색(Binary Search)을 힌트를 사용해 문제를 풀었다.시간복잡도는 S=sum(batteries) // n일 때 $O(n\\, log S)$이다.오랜만에 본 이진탐색과 그리디 알고리
48.leetcode-3623. Count Number of Trapezoids I
1. 문제 소개 3623. Count Number of Trapezoids I 2. 나의 풀이 3. 다른 풀이 4. 마무리
49.leetcode-3625. Count Number of Trapezoids II
어제 풀었던 문제와 거의 비슷한데, 이 풀이는 조금 더 일반적인 풀이에 가깝다.이번에는 내가 생각했던 풀이가 거의 맞았지만, 사다리꼴을 세다 보니 평행사변형이 중복으로 카운팅이 되었다.그 부분을 제외하면 거의 맞았었다.시간복잡도는 $O(n^2)$이다.
50.leetcode-2211. Count Collisions on a Road

2211\. Count Collisions on a Road배열을 순회해서 충돌하는 횟수를 카운팅했다.중요한 점은 배열의 시작에서 연속적으로 오른쪽으로 이동하는 차들을 추적해야햔다.시간복잡도는 $O(n)$이다.이번에는 첫 풀이는 내 풀이고, 두번째 풀이는 힌트를 보고
51.leetcode-3432. Count Partitions with Even Sum Difference

3432\. Count Partitions with Even Sum Difference문제를 봤을 때에는 배열에 홀수의 개수가 홀짝에 따라 답이 다르다고 생각했고, 그대로 풀었을 때 정답이었다.그러나 시간복잡도가 $O(n)$이라 그런지 매우 느렸다.결국 전체 합이 홀수
52.leetcode-3578. Count Partitions With Max-Min Difference at Most K

3578\. Count Partitions With Max-Min Difference at Most Kdp와 sliding window가 힌트로 주어졌다.너무 오랫만이라 공부를 하며 풀었다.문제를 보면 배열을 순회할 때, 최댓값과 최솟값의 차가 k보다 큰 경우를 나눠야
53.leetcode-239. Sliding Window Maximum
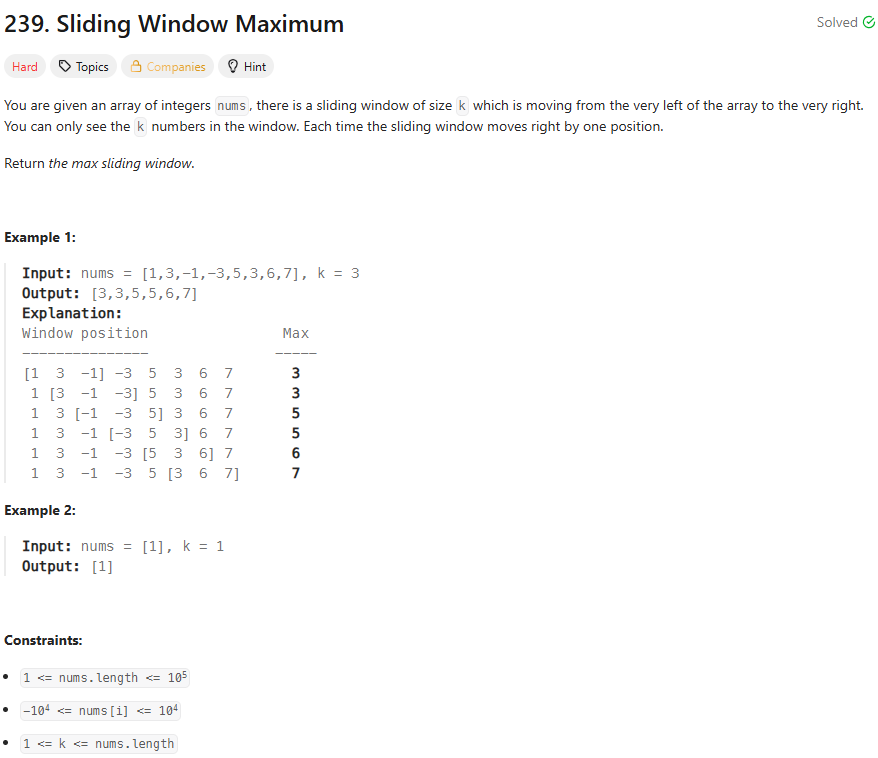
239\. Sliding Window Maximumqueue와 sliding window에 익숙해지기 위해서 풀어보았다.queue를 사용해 최대값과 배열을 관리했다.시간복잡도는 $O(n)$이다.
54.leetcode-1523. Count Odd Numbers in an Interval Range
1523\. Count Odd Numbers in an Interval Range처음에는 range(low, high+1)까지 순회를 할까 생각했지만, high - low + 1 구간을 세는 것이 더 나은 것 같아 바꿔 풀었다.시간복잡도는 $O(1)$이다.쉬운 문제였다
55.leetcode-1925. Count Square Sum Triples

1925\. Count Square Sum Triples푸는 방법은 간단하게 $a^2 + b^2 = c^2$를 적용하면 됐지만, 시간초과가 날까 걱정했다.다행시 시간초과에 걸리지 않았고, 시간복잡도는 $O(n^2)$이다.쉬운 문제였지만 다른 방법을 볼 수 있어 좋았다.
56.leetcode-

3583\. Count Special Triplets문제의 힌트는 빈도수 map을 사용해 배열을 한 번 순회할 때, 숫자 좌우에 나오는 값들을 추적하는 것이다.Counter()를 사용해 순회한 숫자 좌우의 값을 추적해 더해서 풀었다.시간복잡도는 $O(n)$이다.오늘은
57.leetcode-3577. Count the Number of Computer Unlocking Permutations
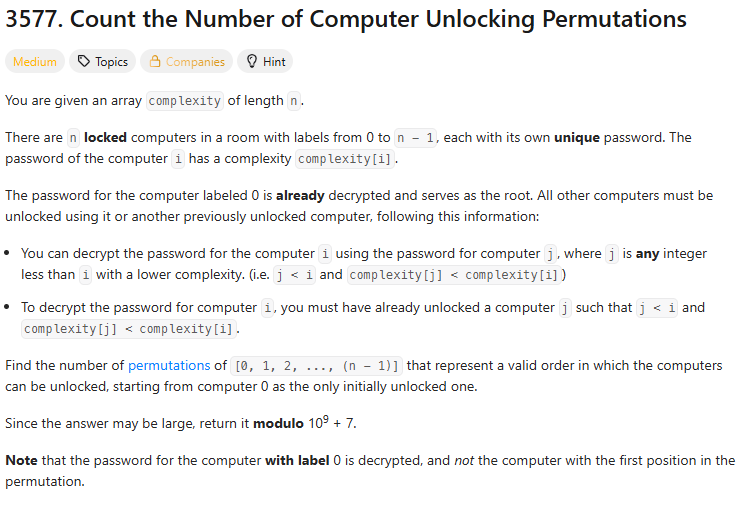
3577\. Count the Number of Computer Unlocking Permutations처음에는 모든 경우를 다 카운팅해야하는 것으로 착각했다.그러나 배열에서 0번째 복잡도보다 작은 복잡도가 나오는 순간 문제의 조건이 어긋나고, 나타나지 않는다면 항상
58.leetcode-3531. Count Covered Buildings

3531\. Count Covered Buildings처음에는 dict를 사용해 x축, y축마다 정리해 풀려고 했었다.그러나 좌표별로 최대값과 최소값을 정리해두고 푸는 것이 낫다는 것을 확인하고 아래와 같이 풀었다.전체 빌딩 수를 $m$이라고 할 때, 시간복잡도는 $O
59.leetcode-3433. Count Mentions Per User
3433\. Count Mentions Per User백엔드와 관련된 문제인 것 같다.힌트를 보지 않고 문제의 조건에 맞게 풀어보았다.코드가 지저분한데, 다른 풀이를 보고 깔끔하게 푸는 것을 목표로 해야겠다.시간복잡도는 최악의 경우 $O(m\\, log m+ m\*n)
60.leetcode-3606. Coupon Code Validator

3606\. Coupon Code Validator배열을 순회할 때 조건에 맞는 경우만 추출하고, 우선도 맵을 사용해서 정렬을 손쉽게 했다.쿠폰 수를 $n$, 평균 쿠폰 코드 길이를 $L$이라고 할 때, 시간복잡도는 $O(n \* L + n\\, log n)$이다.비즈
61.leetcode-2147. Number of Ways to Divide a Long Corridor
2147\. Number of Ways to Divide a Long Corridor의자의 개수가 홀수거나 없는 경우 등의 엣지 케이스를 제외하고, 짝수인 경우만 계산한다.이때 경우의 수에 더하는 것이 아니라 곱하는 것이 포인트였다.시간복잡도는 $O(n)$이다.Edit
62.leetcode-2110. Number of Smooth Descent Periods of a Stock
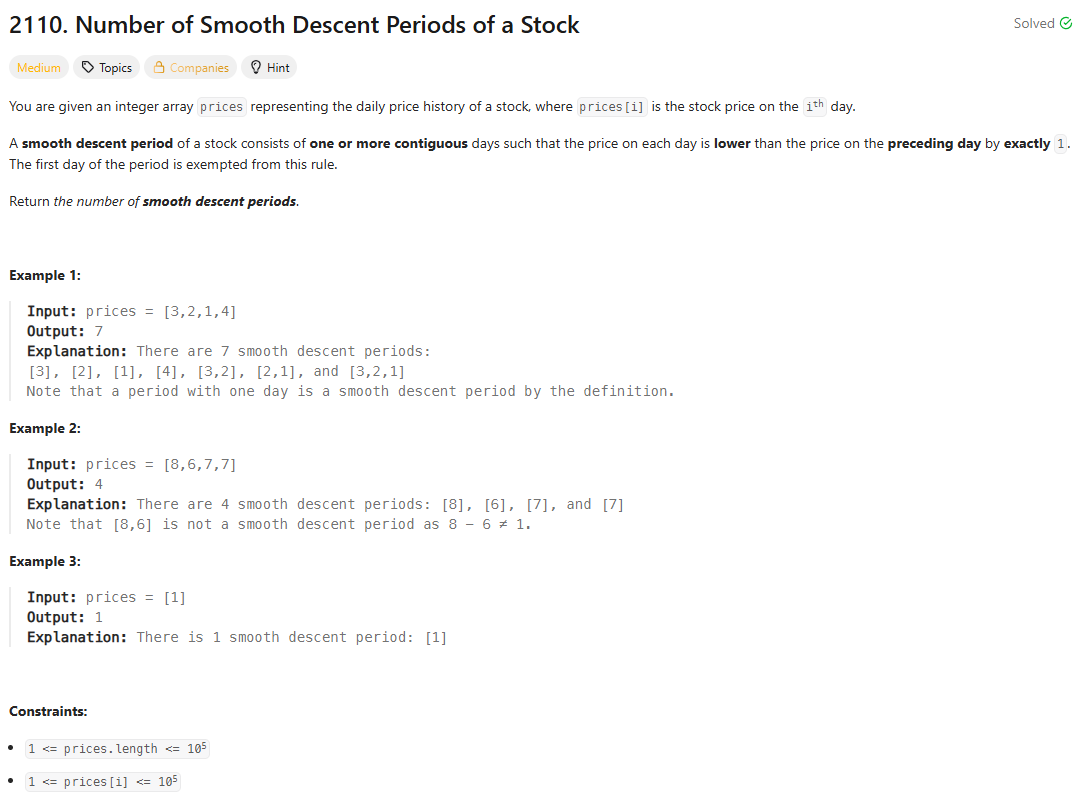
2110\. Number of Smooth Descent Periods of a Stock배열을 순회하며 문제의 조건에 맞는 부분을 찾고, 부분배열의 숫자의 팩토리얼만큼 늘어난다는 사실을 발견했다.풀이의 시간복잡도는 $O(n)$이다.어렵지 않은 문제였다.
63.leetcode-3562. Maximum Profit from Trading Stocks with Discounts

3562\. Maximum Profit from Trading Stocks with Discounts혼자 힘으로 풀지 못했다.dfs와 dp를 사용한 다른 풀이를 보았다.사실 아래 풀이를 다 이해하지도 못했다.이번 문제는 손도 못대 슬프다.
64.leetcode-3573. Best Time to Buy and Sell Stock V

1. 문제 소개 3573. Best Time to Buy and Sell Stock V 2. 나의 풀이 조금 지쳐서 혼자 힘으로 풀지 못했다. 3. 다른 풀이 dp를 사용하여 풀이가 이루어졌다. 사실 혼자 생각해서 풀 수 있는 문제였고, 욕심이 생겼지만 풀지 못했다
65.leetcode-3652. Best Time to Buy and Sell Stock using Strategy

3652\. Best Time to Buy and Sell Stock using Strategy처음에는 모든 합을 구한 다음에, 변화량만 추적했었다.코드 자체는 맞게 풀었지만 시간초과로 인해 틀리고 말았다.
66.leetcode-2092. Find All People With Secret
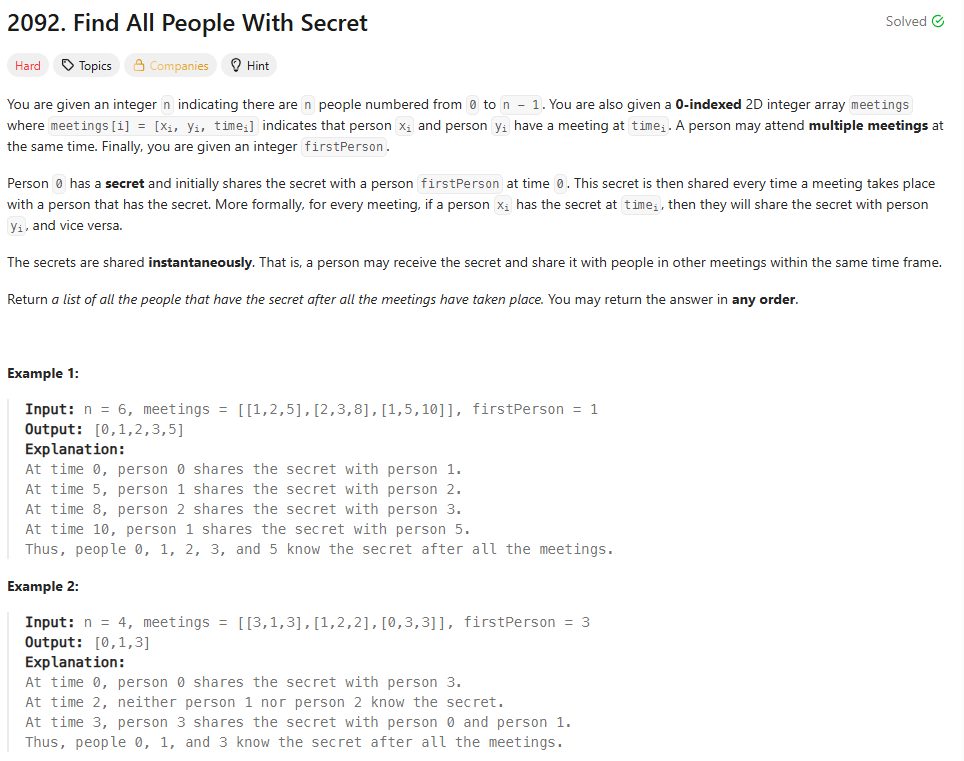
2092\. Find All People With Secret이 문제가 어려움 난이도인 이유는 아무래도 시간제한인 것 같다.처음에는 아주 단순하게 생각했는데, 시행착오를 조금 겪은 이후에는 bfs를 떠올렸다.그리고 시간초과로 인해 틀리고 말았다.다른 풀이는 Union-
67.leetcode-

944\. Delete Columns to Make Sorted첫 시도에서는 grid로 만들어 풀었고, 필요없는 집합도 사용해 속도가 좋지 않았다.이 경우 시간복잡도는 $O(n \* m)$이다.처음에 문제를 잘못 읽어서 쓸데없이 복잡하게 푼 것이 아쉽다.
68.leetcode-955. Delete Columns to Make Sorted II

955\. Delete Columns to Make Sorted II처음에는 문제를 바로 이해하지 못했다.문제의 의미는 결국 주어진 문자열들이 사전순서로 배치되었는가, 아닌가를 체크하는 것이다.Greedy Algorithm을 사용하여 풀었다.시간복잡도는 $O(n \*
69.leetcode-960. Delete Columns to Make Sorted III
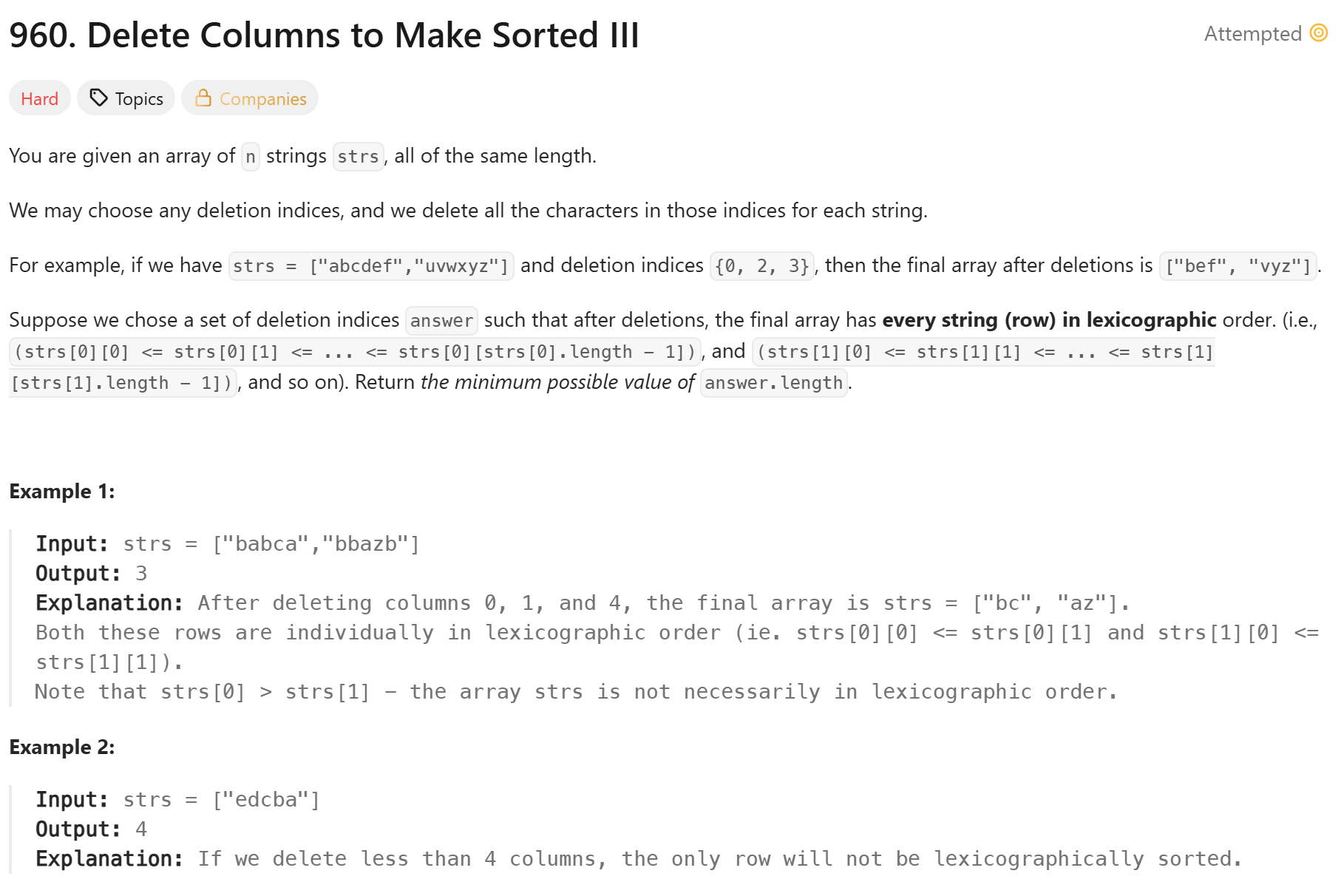
960\. Delete Columns to Make Sorted III처음에는 이전과 비슷한 방법을 사용했으나 dp를 사용했다.시간복잡도는 $O(n^2 \* m)$이다.
70.leetcode-2054. Two Best Non-Overlapping Events

2054\. Two Best Non-Overlapping Events내 힘으로는 풀지 못했다.Editorial의 풀이는 다음과 같다.dp와 binary search를 사용한 풀이였다.시간복잡도는 $O(N log N)$이다.
71.leetcode-3074. Apple Redistribution into Boxes
3074\. Apple Redistribution into Boxes쉬운 문제인 만큼 간단하게 풀 수 있었다.시간복잡도는 $O(k\\, \\text{log} k)$이다.
72.leetcode-3075. Maximize Happiness of Selected Children
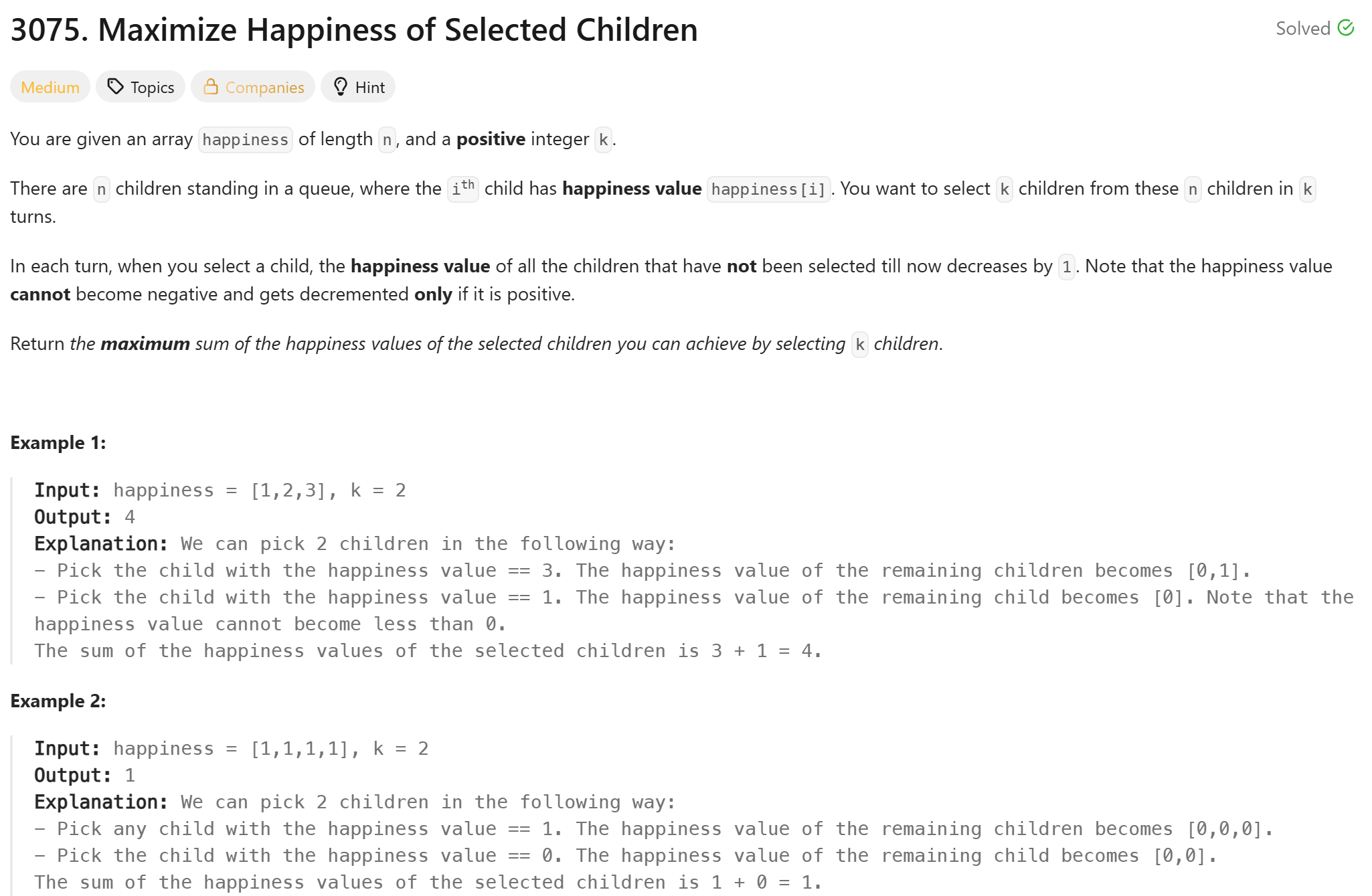
3075\. Maximize Happiness of Selected Children순간순간의 최고의 선택이 결국 최적해가 된다는 Greedy Algorithm을 적용해 바로 풀었다.시간복잡도는 정렬에 쓰인 $O(n\\, log n)$이다.시간복잡도 측면에서는 정렬이 힙
73.Leetcode-100 Days Badge 2025

74.leetcode-2483. Minimum Penalty for a Shop

2483\. Minimum Penalty for a Shopprefix와 suffix를 사용해 풀었다.시간복잡도는 $O(n)$이다.
75.leetcode-2402. Meeting Rooms III
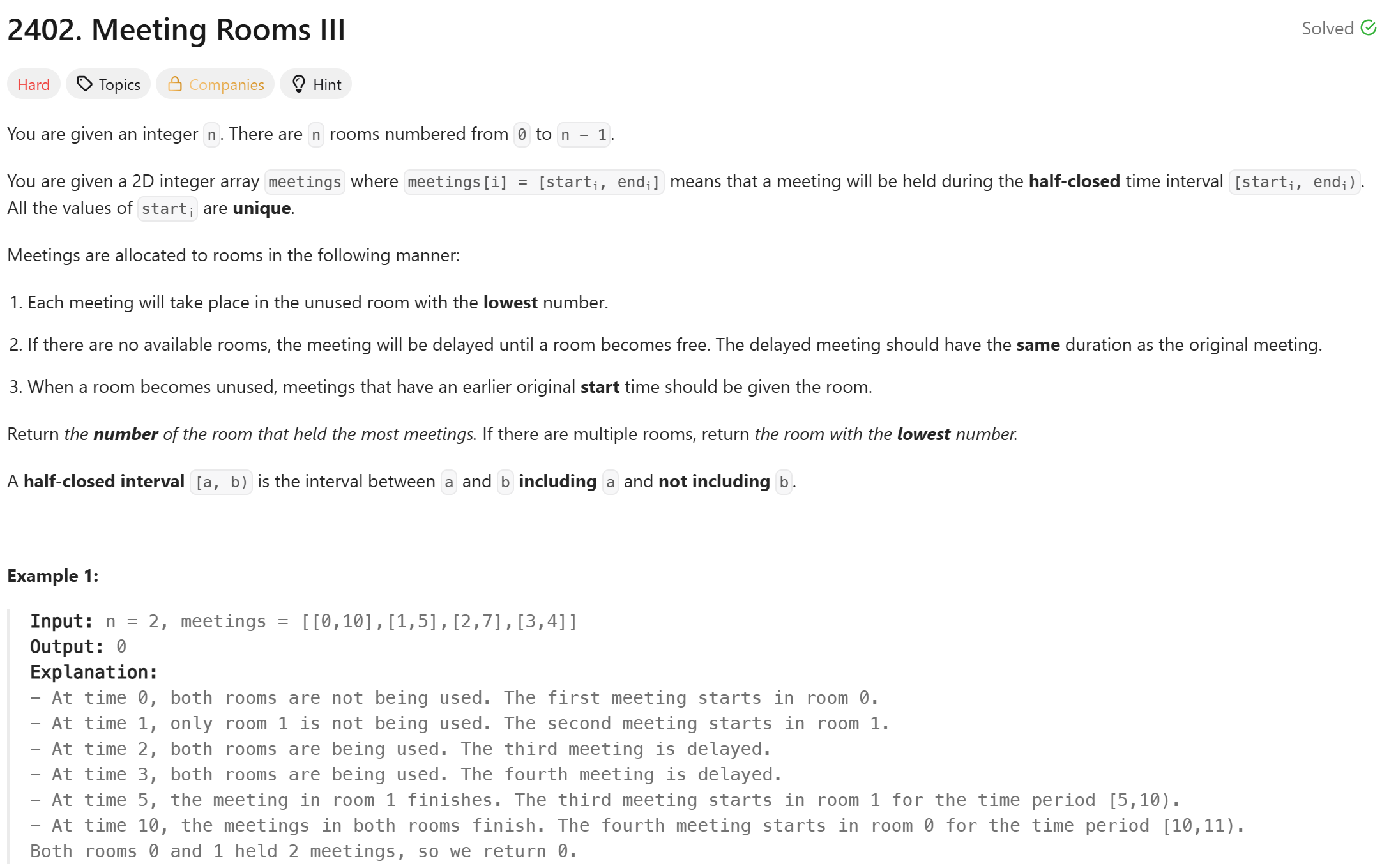
2402\. Meeting Rooms III풀지 못했다.Editorial의 풀이는 다음과 같다.시간복잡도는 $O(M log M + M \* n)$이다.
76.leetcode-1351. Count Negative Numbers in a Sorted Matrix

1351\. Count Negative Numbers in a Sorted Matrix이분탐색을 이용한 풀이다.시간복잡도는 $O(n \* log m)$이다.
77.leetcode-756. Pyramid Transition Matrix

756\. Pyramid Transition Matrixdfs를 사용해 풀었는데, 다른 풀이를 보고 푼 것이라 헷갈린다.
78.leetcode-840. Magic Squares In Grid

840\. Magic Squares In Grid어려운 문제라기보다는 엣지 케이스를 잘 고려해야하는 문제였다.시간복잡도는 $O(n\\times m)$이다.
79.leetcode-1970. Last Day Where You Can Still Cross

1970\. Last Day Where You Can Still Cross문제는 BFS와 Binary Search를 동시에 적용했다.만약 3번째 날에 땅을 횡단할 수 있다면 이전에도 횡단할 수 있다는 것이고, 횡단할 수 없다면 이후에도 횡단할 수 없다는 의미이다.따라서
80.leetcode-66. Plus One
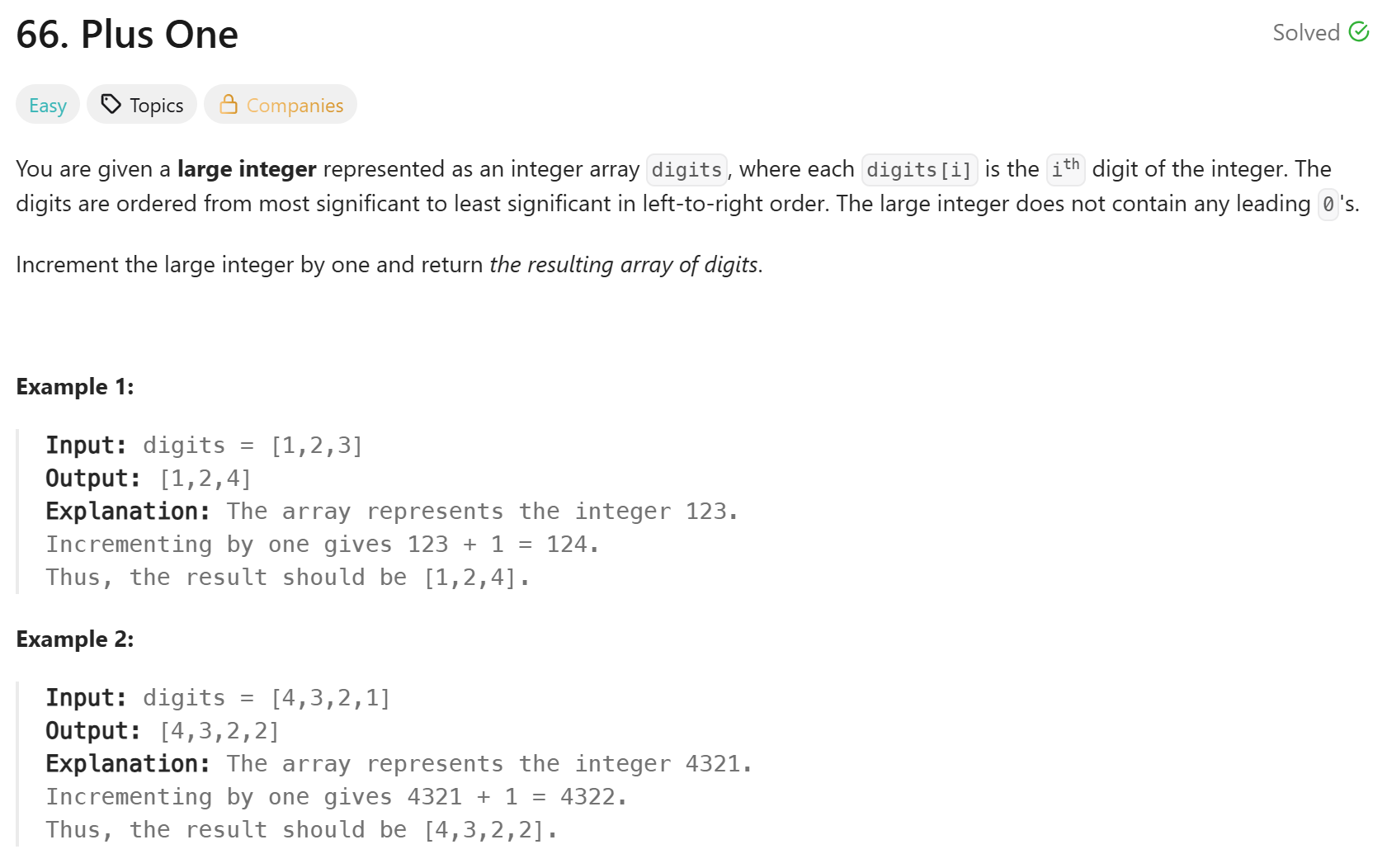
66\. Plus One다행히 쉬운 풀이였다.숫자로 만든 이후에 다시 배열로 바꾸었다.시간복잡도는 $O(n)$이다.
81.leetcode-961. N-Repeated Element in Size 2N Array

961\. N-Repeated Element in Size 2N Array처음에는 Counter()를 사용해서 풀려고 시도했다.그러나 value를 통해 key를 찾는 방법이 바로 기억나지 않아서 다시 순회를 하는 바람에 늦어졌다.시간복잡도는 $O(n)$이다.쉬운 문제였
82.leetcode-1411. Number of Ways to Paint N × 3 Grid

1411\. Number of Ways to Paint N × 3 Grid조합론에 가까운 풀이로 경우를 나눠 점화식을 사용해 풀었다.모두 다른 색깔을 사용하는 경우와 똑같은 색깔이 있는 경우를 나누면 된다.
83.leetcode-1390. Four Divisors
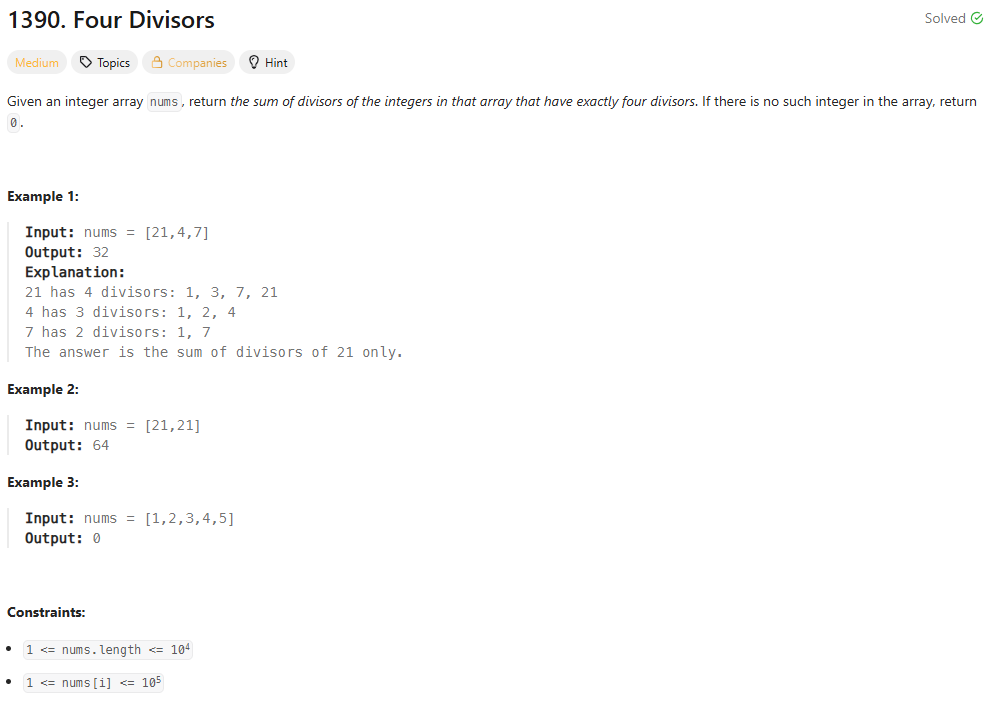
1390\. Four Divisors$\\sqrt{n}$만큼만 약수를 확인하면 되며 약수의 개수가 4개를 넘어가면 중단하는 방식으로 속도를 높였다.
84.leetcode-1975. Maximum Matrix Sum

1975\. Maximum Matrix Sum문제에 나온 규칙대로라면 음수의 개수에 따라 답이 달라진다.음수의 개수가 짝수라면 그냥 모든 entry의 절대값을 더하고, 홀수라면 절대값이 가장 낮은 것만 세면 된다.다른 문제들도 이와 같은 로직을 사용해 풀었다.시간복잡도
85.leetcode-1161. Maximum Level Sum of a Binary Tree
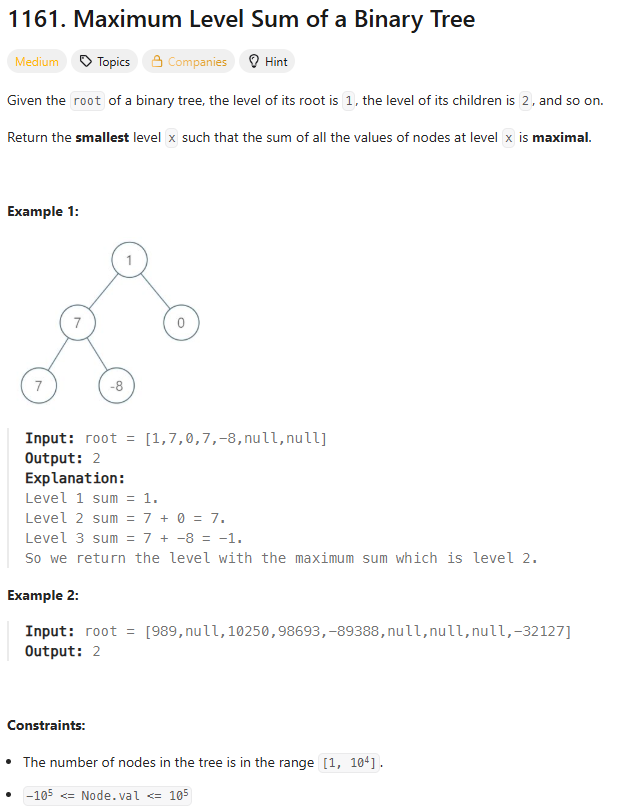
1161\. Maximum Level Sum of a Binary Tree간단하게 bfs를 사용해 풀었다.시간복잡도는 $O(n)$이다.dfs를 사용한 풀이도 있다는 것이 조금 놀라웠다.직관적으로는 bfs가 맞다고 생각하지만 dfs도 맞는 방향으로 갈 수 있었다.
86.leetcode-1339. Maximum Product of Splitted Binary Tree
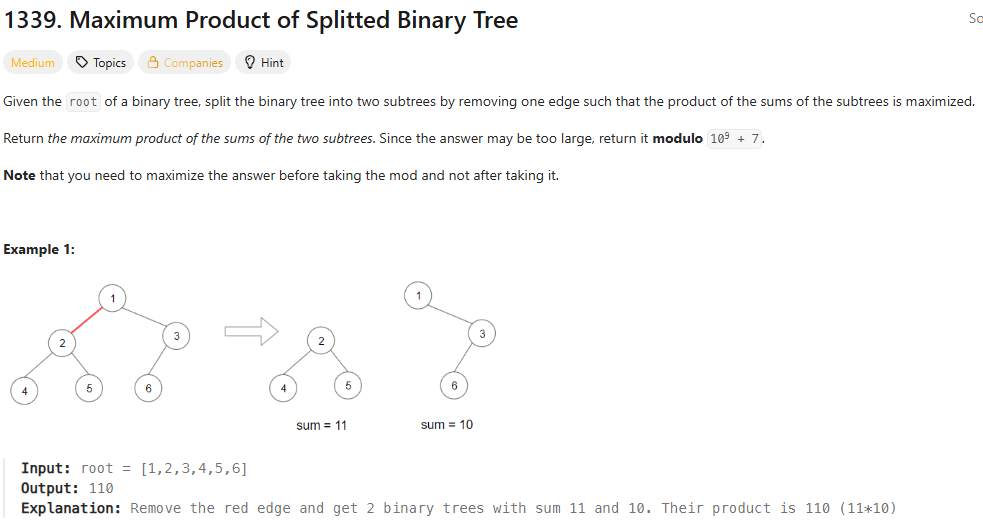
1339\. Maximum Product of Splitted Binary Tree힌트를 보며 풀었는데, dfs를 통해 이진트리의 합을 구하고, 부분합과 총합의 차를 계산하며 푸는 방식이다.모든 노드를 한 번씩 방문해 시간복잡도는 $O(n)$이다.
87.leetcode-1266. Minimum Time Visiting All Points

1266\. Minimum Time Visiting All PointsGreedy Algorithm으로 각각의 최소 거리의 합이 곧 모든 점들의 최소 이동거리이다.
88.leetcode-3650. Minimum Cost Path with Edge Reversals

3650\. Minimum Cost Path with Edge Reversals다익스트라를 사용한 방법이다.시간복잡도는 $O((n + m) \\text{log}\\, n)$이다.
89.leetcode-3651. Minimum Cost Path with Teleportations

3651\. Minimum Cost Path with Teleportations혼자 풀지 못해서 풀이를 참조했다.시간복잡도는 $O((k+1) m n)$이다.
90.leetcode-2976. Minimum Cost to Convert String I
2976\. Minimum Cost to Convert String I시간복잡도는 $O(26^3 + |\\text{source}|)$이다.
91.leetcode-744. Find Smallest Letter Greater Than Target

744\. Find Smallest Letter Greater Than Target한 번 순회하는 방식으로 계산했다.시간복잡도는 $O(n)$이다.