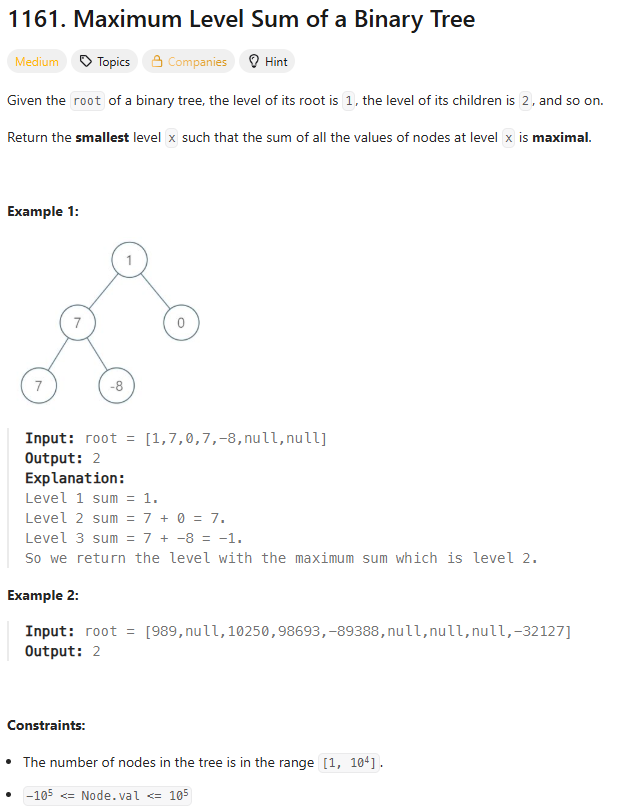
1. 문제 소개

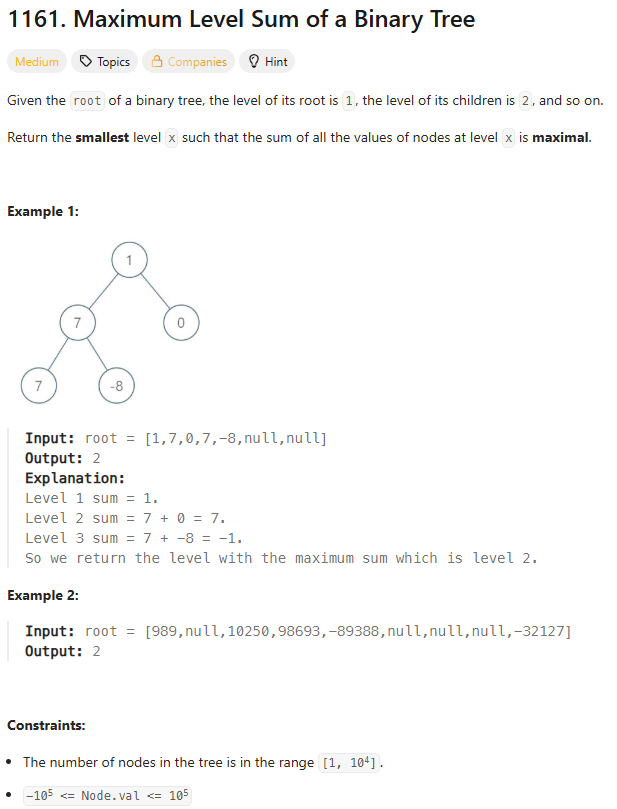
1161. Maximum Level Sum of a Binary Tree

2. 나의 풀이

간단하게 bfs를 사용해 풀었다.
시간복잡도는 $O(n)$이다.

class Solution:                                                   # LeetCode 제출을 위한 Solution 클래스 정의
    def maxLevelSum(self, root: Optional[TreeNode]) -> int:       # 최대 레벨 합을 가지는 레벨 번호를 반환하는 함수
        ans = 1                                                   # 최대 합을 가진 레벨 번호를 저장할 변수 초기화
        cur_lvl = 1                                               # 현재 탐색 중인 레벨 번호 초기화
        cur_max = -10**6                                          # 레벨 합의 최댓값을 저장할 변수 초기화
        
        q = deque([root])                                         # BFS를 위한 큐에 루트 노드를 초기 상태로 삽입

        while q:                                                  # 큐가 빌 때까지 레벨 단위로 반복
            cur_sum = 0                                           # 현재 레벨의 노드 값 합을 저장할 변수
            cur_size = len(q)                                     # 현재 레벨에 포함된 노드 개수 저장

            for _ in range(cur_size):                             # 현재 레벨의 모든 노드를 처리
                node = q.popleft()                                # 큐에서 하나의 노드를 꺼냄
                cur_sum += node.val                               # 해당 노드의 값을 현재 레벨 합에 더함

                if node.left:                                     # 왼쪽 자식이 존재하는 경우
                    q.append(node.left)                           # 다음 레벨 탐색을 위해 큐에 추가
                if node.right:                                    # 오른쪽 자식이 존재하는 경우
                    q.append(node.right)                          # 다음 레벨 탐색을 위해 큐에 추가
                
            if cur_sum > cur_max:                                 # 현재 레벨 합이 기존 최대값보다 큰 경우
                cur_max = cur_sum                                 # 최대 합을 현재 레벨 합으로 갱신
                ans = cur_lvl                                     # 최대 합을 만든 레벨 번호로 갱신
            
            cur_lvl += 1                                          # 다음 레벨로 이동하기 위해 레벨 번호 증가

        return ans                                                # 최대 레벨 합을 가진 레벨 번호 반환

3. 다른 풀이

dfs를 사용한 풀이도 존재한다.
시간복잡도는 $O(n)$이다.

class Solution:                                                        # LeetCode 제출용 Solution 클래스 정의
    def dfs(                                                           # DFS를 이용해 레벨별 노드 합을 누적하는 함수 정의
        self, node: Optional[TreeNode], level: int, sum_of_nodes_at_level: List[int]
    ) -> None:
        if node is None:                                               # 현재 노드가 None이면 더 탐색할 필요 없으므로 종료
            return                                                     # 재귀 호출 종료

        if len(sum_of_nodes_at_level) == level:                        # 현재 레벨이 처음 등장한 경우
            sum_of_nodes_at_level.append(node.val)                     # 해당 레벨의 합을 노드 값으로 초기화
        else:                                                          # 이미 해당 레벨이 존재하는 경우
            sum_of_nodes_at_level[level] += node.val                   # 해당 레벨의 합에 현재 노드 값을 누적

        self.dfs(node.left, level + 1, sum_of_nodes_at_level)          # 왼쪽 자식 노드를 다음 레벨로 DFS 호출
        self.dfs(node.right, level + 1, sum_of_nodes_at_level)         # 오른쪽 자식 노드를 다음 레벨로 DFS 호출

    def maxLevelSum(self, root: Optional[TreeNode]) -> int:             # 최대 레벨 합을 가지는 레벨 번호를 반환하는 함수
        sum_of_nodes_at_level = []                                      # 레벨별 노드 합을 저장할 리스트 초기화
        self.dfs(root, 0, sum_of_nodes_at_level)                        # 루트부터 레벨 0 기준으로 DFS 시작

        max_sum = float("-inf")                                         # 현재까지의 최대 레벨 합을 저장할 변수 초기화
        ans = 0                                                        # 최대 합을 가지는 레벨의 인덱스를 저장할 변수

        for i in range(len(sum_of_nodes_at_level)):                    # 모든 레벨을 순회하며
            if max_sum < sum_of_nodes_at_level[i]:                     # 현재 레벨 합이 최대값보다 큰 경우
                max_sum = sum_of_nodes_at_level[i]                     # 최대 합을 현재 레벨 합으로 갱신
                ans = i + 1                                            # 레벨 번호는 1-indexed이므로 i + 1로 저장

        return ans                                                      # 최대 레벨 합을 가지는 레벨 번호 반환

4. 마무리

dfs를 사용한 풀이도 있다는 것이 조금 놀라웠다.
직관적으로는 bfs가 맞다고 생각하지만 dfs도 맞는 방향으로 갈 수 있었다.