1. 문제 소개

1590. Make Sum Divisible by P

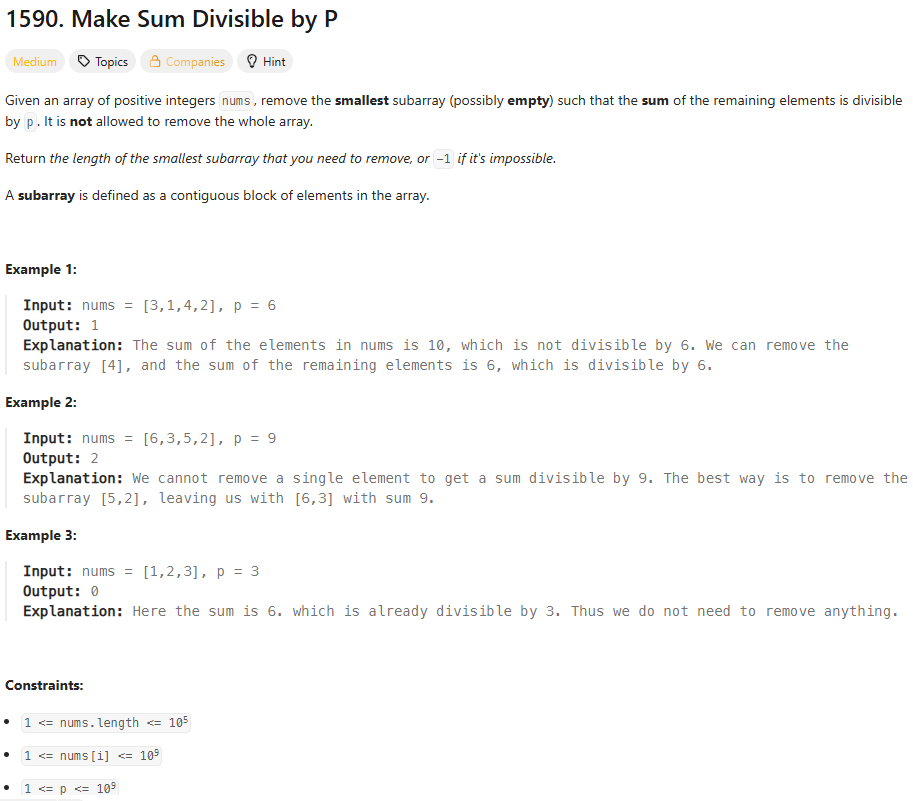
2. 나의 풀이

오늘은 풀이가 잘 생각나지 않아 Editorial을 참고했다.
시간복잡도는 $O(n)$이다.

class Solution:
    def minSubarray(self, nums: List[int], p: int) -> int:
        n = len(nums)                     # 배열 길이
        total = 0                         # 전체 합의 p에 대한 나머지를 누적할 변수

        for num in nums:                  # nums 전체를 순회하며
            total = (total + num) % p     # 전체 합의 나머지를 누적 (overflow 방지용 mod)

        target = total % p                # 제거해야 하는 subarray의 합이 가져야 할 나머지
        if target == 0:                   # 이미 전체 합이 p로 나누어떨어지면
            return 0                      # 아무 subarray도 제거할 필요 없음

        mod_map = {0: -1}                 # prefix mod → 가장 최근 index
                                          # prefix sum == 0 (mod p) 를 '인덱스 -1'에서 출발한다고 가정

        cur = 0                           # 현재 prefix sum의 나머지 (0부터 시작)
        min_len = n                       # 제거할 subarray 길이의 최솟값 (최대 n으로 초기화)

        for i in range(n):
            cur = (cur + nums[i]) % p     # nums[0..i]까지의 prefix sum % p

            need = (cur - target + p) % p # sum(l..i) % p == target 이 되려면
                                          # prefix[l-1] % p == need 여야 한다.

            if need in mod_map:           # 과거에 같은 need 나머지를 가진 prefix가 있었다면
                min_len = min(min_len, i - mod_map[need])
                # 그 prefix 이후부터 현재 i까지의 subarray가 제거 후보 (길이: i - mod_map[need])

            mod_map[cur] = i              # 현재 prefix 나머지를 최신 index로 기록 (가장 최근 값이 길이 최소에 유리)

        return -1 if min_len == n else min_len
        # min_len이 한 번도 갱신되지 않았다면 제거 가능한 subarray가 없음 → -1
        # 그렇지 않다면 min_len이 요구 조건을 만족하는 최소 길이

3. 다른 풀이

모든 풀이가 위와 같은 알고리즘이었다.

4. 마무리

오늘은 혼자 힘으로 하지 못해 아쉽다.