1. 문제 소개

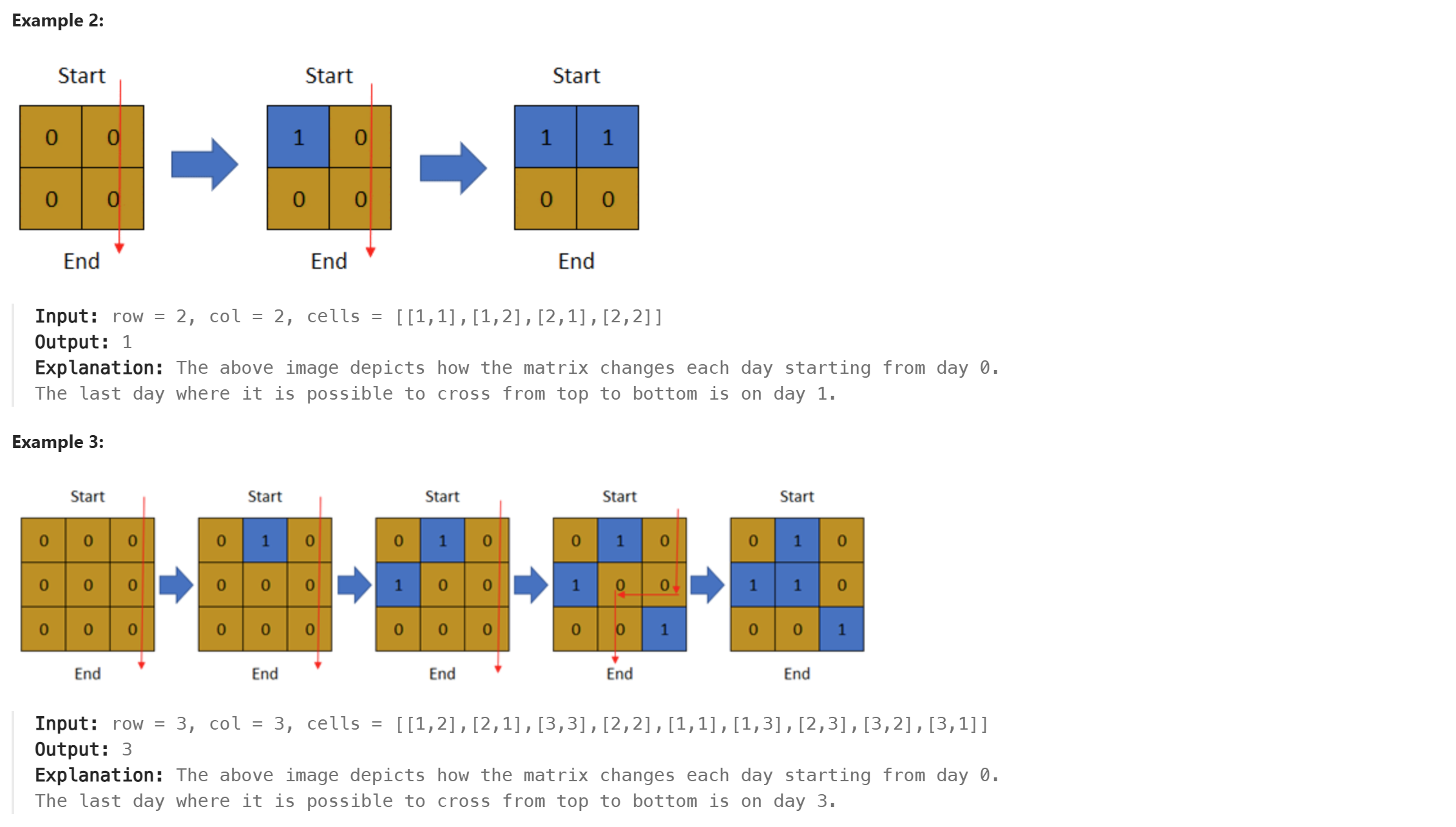
1970. Last Day Where You Can Still Cross

2. 나의 풀이

문제는 BFS와 Binary Search를 동시에 적용했다.
만약 3번째 날에 땅을 횡단할 수 있다면 이전에도 횡단할 수 있다는 것이고, 횡단할 수 없다면 이후에도 횡단할 수 없다는 의미이다.
따라서 이분탐색을 통해 적절한 day를 고르고, BFS를 통해 횡단이 가능한 지 체크하는 풀이다.
시간복잡도는 $O(row×col×\text{log}(row×col))$이다.

class Solution:
    def latestDayToCross(self, row: int, col: int, cells: List[List[int]]) -> int:     
        def bfs(day):
            land = [[True] * col for _ in range(row)]          # True=land, False=water로 사용할 격자 초기화(전부 land)

            for i in range(day):                               # day일 동안 물이 되는 칸을 반영
                r, c = cells[i][0] - 1, cells[i][1] - 1        # 입력이 1-indexed이므로 0-index로 변환
                land[r][c] = False                             # 해당 칸을 water로 변경

            q = deque()                                        # BFS 큐
            visited = [[False] * col for _ in range(row)]      # 방문 체크

            for c in range(col):                               # 0행의 모든 열에서 시작 가능 지점 탐색
                if land[0][c]:                                 # land인 칸만 시작점
                    q.append((0, c))                            # 시작점 큐에 삽입
                    visited[0][c] = True                        # 방문 처리

            dirs = [(1,0), (0,1), (-1,0), (0,-1)]              # 4방향 이동

            while q:
                r, c = q.popleft()                             # 현재 위치 pop

                if r == row - 1:                               # 마지막 행에 도달하면
                    return True                                 # crossing 가능

                for dr, dc in dirs:                             # 4방향 확장
                    nr, nc = r + dr, c + dc

                    if 0 <= nr < row and 0 <= nc < col and land[nr][nc] and not visited[nr][nc]:
                        visited[nr][nc] = True                 # 미방문 land면 방문 처리
                        q.append((nr, nc))                     # 큐에 삽입

            return False                                        # BFS 종료까지 마지막 행을 못 갔으면 crossing 불가

        left, right = 1, len(cells)                             # 이분 탐색 범위: day(1..row*col)
        ans = 0                                                 # 마지막으로 가능한 day 기록(초기 0)

        while left <= right:
            mid = (left + right) // 2                           # 현재 검사할 day

            if bfs(mid):                                        # mid day에 crossing 가능하면
                ans = mid                                       # 후보 갱신
                left = mid + 1                                  # 더 큰 day를 탐색(마지막 True 찾기)
            else:                                               # crossing 불가하면
                right = mid - 1                                 # 더 작은 day로 이동

        return ans                                               # 마지막으로 가능했던 day 반환

3. 다른 풀이

처음 생각했던 풀이는 다음과 같다.
결국 water가 가득 차 land를 2개로 분할하는 것을 찾는 문제로 해석한 Union-Find 알고리즘이다.
이 알고리즘을 잘 몰라서 찾아만 왔다.

class Solution:
    def latestDayToCross(self, row: int, col: int, cells: List[List[int]]) -> int:
        n = row * col                                     # 전체 셀 개수
        top, bottom = n, n + 1                            # 가상 노드: top(윗줄), bottom(아랫줄)

        parent = list(range(n + 2))                       # Union-Find parent 배열
        rank = [0] * (n + 2)                              # Union-Find rank 배열
        grid = [[False] * col for _ in range(row)]        # 현재 land 여부(False=water, True=land)

        def find(x):
            if parent[x] != x:                            # 경로 압축
                parent[x] = find(parent[x])
            return parent[x]

        def union(a, b):
            a, b = find(a), find(b)                       # 두 노드의 루트 찾기
            if a == b:
                return                                   # 이미 같은 컴포넌트면 종료
            if rank[a] < rank[b]:                         # rank 기준 union
                parent[a] = b
            else:
                parent[b] = a
                if rank[a] == rank[b]:
                    rank[a] += 1

        dr = [1, -1, 0, 0]                                # 상하좌우 이동 벡터
        dc = [0, 0, 1, -1]

        # day를 역순으로 순회하며 land를 하나씩 "복구"
        for d in range(n - 1, -1, -1):
            r, c = cells[d][0] - 1, cells[d][1] - 1       # 1-indexed → 0-indexed
            grid[r][c] = True                             # 해당 칸을 land로 변경
            idx = r * col + c                             # 2D 좌표를 1D 인덱스로 변환

            if r == 0:                                    # 맨 윗줄이면 top 가상 노드와 연결
                union(idx, top)
            if r == row - 1:                              # 맨 아랫줄이면 bottom 가상 노드와 연결
                union(idx, bottom)

            # 인접한 land들과 union
            for k in range(4):
                nr, nc = r + dr[k], c + dc[k]
                if 0 <= nr < row and 0 <= nc < col and grid[nr][nc]:
                    union(idx, nr * col + nc)

            # top과 bottom이 연결되면 crossing 가능
            if find(top) == find(bottom):
                return d                                  # 역순이므로 d가 정답 day

        return 0                                          # 이론상 도달하지 않음

4. 마무리

어려운 문제였지만 힌트를 보고 잘 풀었다.
2개의 다른 아이디어가 존재해 좋았다.