1. 문제 소개

2435. Paths in Matrix Whose Sum Is Divisible by K

2. 나의 풀이

처음에는 dfs로 풀려고 시도했으나 dp가 맞는 방향이라는 힌트를 보고 방법을 바꿨다.
단순하게 2차원 배열을 시도했지만 3차원 배열이 필요하다는 것을 깨닫고, 정답코드를 봐가며 풀었다.
시간복잡도는 $O(m * n * k)$이다.

class Solution:
    def numberOfPaths(self, grid: List[List[int]], k: int) -> int:
        MOD = 10 ** 9 + 7
        m, n = len(grid), len(grid[0])

        # dp 배열 크기:
        # - 행: 0 ~ m (총 m+1)
        # - 열: 0 ~ n (총 n+1)
        # - 나머지 상태: 0 ~ k-1 (총 k개)
        # dp[i][j][r] = (i, j)에 도달했을 때, 경로 합 % k == r 인 경우의 수
        # i, j는 1-based 좌표로 해석하고, 실제 grid 접근은 grid[i-1][j-1]로 한다.
        dp = [[[0] * k for _ in range(n + 1)] for _ in range(m + 1)]

        for i in range(1, m+1):               # 1 ~ m
            for j in range(1, n+1):           # 1 ~ n
                if i == 1 and j == 1:
                    # 시작점 (0,0)에 해당하는 1-based 좌표 (1,1)
                    # 이 위치의 값 grid[0][0]을 더했을 때, 나머지 상태는 grid[0][0] % k
                    # 그 상태로 가는 경로는 단 하나(시작점 자체)이다.
                    dp[i][j][grid[0][0] % k] = 1
                    continue
                
                value = grid[i-1][j-1] % k    # 현재 칸 값의 나머지 (이 칸을 더할 때의 증가량)
                for r in range(k):            # 현재 칸에 도달했을 때 가지게 될 나머지 상태 r
                    # 현재 칸에서의 r 상태를 만들기 직전의 나머지 상태(prev_mod)를 역산한다.
                    # (prev_mod + value) % k == r  ⇒  prev_mod == (r - value + k) % k
                    prev_mod = (r - value + k) % k

                    # 위쪽에서 내려오는 경우: (i-1, j)에서 prev_mod 상태로 도착했던 경로 수
                    # 왼쪽에서 오는 경우: (i, j-1)에서 prev_mod 상태로 도착했던 경로 수
                    # 둘 다 이 칸의 value를 더해 r 상태가 되므로 합쳐서 dp[i][j][r]에 더한다.
                    dp[i][j][r] = (dp[i - 1][j][prev_mod] + dp[i][j - 1][prev_mod]) % MOD
        
        # 최종 목적지 (m, n)에 도달하는 경로들 중
        # "경로합 % k == 0" 인 경우의 수가 우리가 원하는 정답.
        return dp[m][n][0]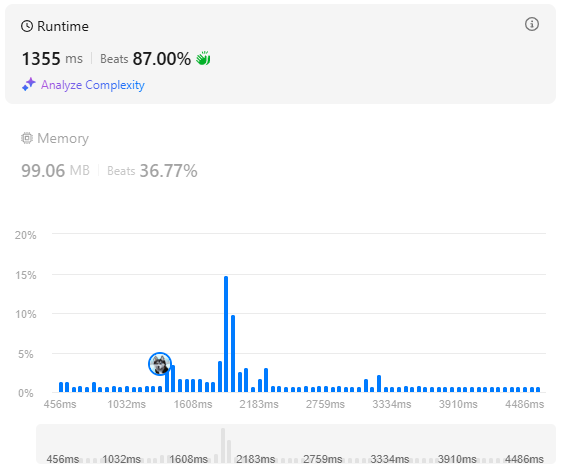

3. 다른 풀이

시간복잡도는 $O(m * n * k)$이다.

class Solution:
    def numberOfPaths(self, grid: List[List[int]], k: int) -> int:
        MOD = 10**9 + 7
        m, n = len(grid), len(grid[0])

        # prev[j][r]  : 이전 행(i-1)의 j번째 열에 도달했을 때, (sum % k == r)인 경로 수
        # curr[j][r]  : 현재 행(i)의 j번째 열에 도달했을 때, (sum % k == r)인 경로 수
        prev = [[0]*k for _ in range(n)]
        curr = [[0]*k for _ in range(n)]

        # 첫 번째 행(0번째 행)의 prefix 경로 처리
        # (0,0) → (0,j)로 가는 경로는 오른쪽으로만 진행하므로 경로가 단 1개이다.
        s = 0
        for j in range(n):
            s = (s + grid[0][j]) % k        # 첫 행의 누적 합의 나머지
            prev[j][s] = 1                 # 해당 나머지 상태로 가는 경로는 1개

        # 첫 행 처리가 끝난 상태에서,
        # 첫 번째 열(각 행의 (i,0)) prefix 나머지 초기화 준비
        s = grid[0][0] % k

        for i in range(1, m):
            # 현재 행 i의 첫 번째 칸 (i,0): 위에서만 내려올 수 있음
            s = (s + grid[i][0]) % k       # 위에서 누적된 prefix sum을 기반으로 갱신
            curr[0] = [0]*k
            curr[0][s] = 1                 # 왼쪽에서 올 수 없으므로 한 경로만 존재

            # 현재 행의 나머지 열들 j = 1..n-1
            for j in range(1, n):
                curr[j] = [0]*k            # (i,j)의 모든 나머지 상태를 0으로 초기화

                val = grid[i][j]           # 현재 칸의 값
                for r in range(k):
                    # r은 이전 상태(prev 또는 curr-left)의 "sum % k"
                    # 현재 칸을 더한 후의 새로운 나머지 nr
                    nr = (r + val) % k

                    # (i,j)에 도달하는 경로는 두 방향에서 온다:
                    #   1) 위쪽:   prev[j][r]
                    #   2) 왼쪽:   curr[j-1][r]
                    curr[j][nr] = (prev[j][r] + curr[j - 1][r]) % MOD

            # prev <-> curr swap (다음 행 계산 준비)
            prev, curr = curr, prev

        # 최종 목적지 (m-1, n-1) 까지 도달하는 경로 중
        # 나머지가 0인 경로 수만 결과로 반환
        return prev[n - 1][0]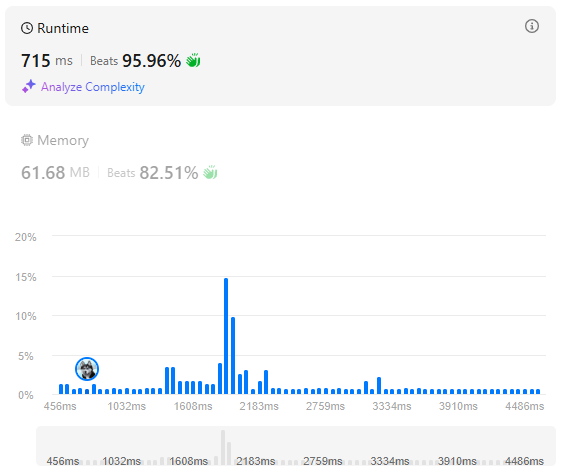

4. 마무리

오늘은 좀 어려워서 힌트를 보았다. 잘 생각했다면 혼자 풀 수 있었는데 아쉽다.