1. 문제 소개

2654. Minimum Number of Operations to Make All Array Elements Equal to 1

2. 나의 풀이

처음 든 생각은 인접한 배열이 서로소가 나온다면 끝나는 풀이라고 생각했다.
배열에 1이 존재한다면 1을 제외한 만큼, 아니라면 배열 전체를 순회해서 gcd가 1이 나올 때까지 반복해야 한다고 생각했다.
시간복잡도는 $O(N^2\,Log(M))$이다.

class Solution:
    def minOperations(self, nums: List[int]) -> int:
        def gcd(a, b):                     # 유클리드 호제법
            while b:
                a, b = b, a % b
            return a
        
        n = len(nums)
        ones = nums.count(1)               # 이미 1인 원소 개수
        if ones:                           # 1이 존재하면, 나머지를 1로 바꾸는 연산만 필요
            return n - ones                # 각 비-1 원소당 1번의 연산으로 인접 1로 변환

        cnt = 10 ** 6                      # 1을 만들기 위한 최소 구간 길이(초기값: 매우 큼)
        for i in range(n):                 # 모든 시작 위치 i 탐색
            g = nums[i]                    # 구간의 시작 GCD
            for j in range(i + 1, n):      # 오른쪽으로 확장
                g = gcd(g, nums[j])        # 누적 GCD 계산
                if g == 1:                 # 구간 [i, j]의 GCD가 1이면,
                    cnt = min(cnt, j - i)  # 그 구간 길이(j - i)가 1을 만드는 최소비용 후보
                    break                  # 더 확장해도 최소 길이는 늘어남 → 중단

        if cnt == 10 ** 6:                 # GCD가 1인 구간이 단 한 번도 없으면
            return -1                      # 어떤 방법으로도 1 생성 불가능
        return cnt + n - 1                 # (1 만드는 데 cnt회) + (전체를 1로 확장하는 n-1회)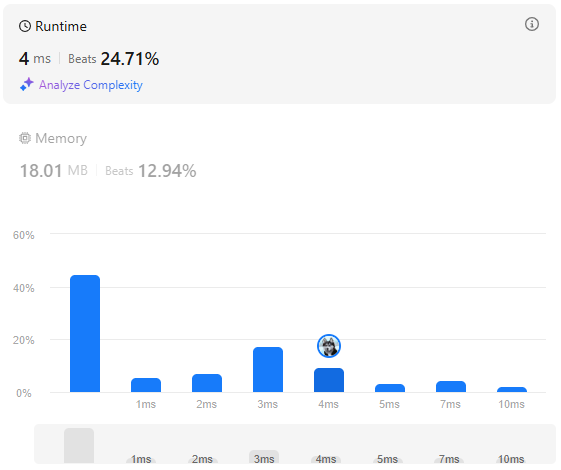

3. 다른 풀이

Editorial의 풀이가 가장 짧은 시간이 걸렸다.
시간복잡도는 동일하지만, 엣지 케이스 설계를 잘해서 그런 것같다.

class Solution:
    def minOperations(self, nums: List[int]) -> int:
        n = len(nums)
        num1 = 0
        g = 0

        for x in nums:
            if x == 1:
                num1 += 1
            g = gcd(g, x)

        if num1 > 0:
            return n - num1
        if g > 1:
            return -1

        min_len = n
        for i in range(n):
            g = 0
            for j in range(i, n):
                g = gcd(g, nums[j])
                if g == 1:
                    min_len = min(min_len, j - i + 1)
                    break

        return min_len + n - 2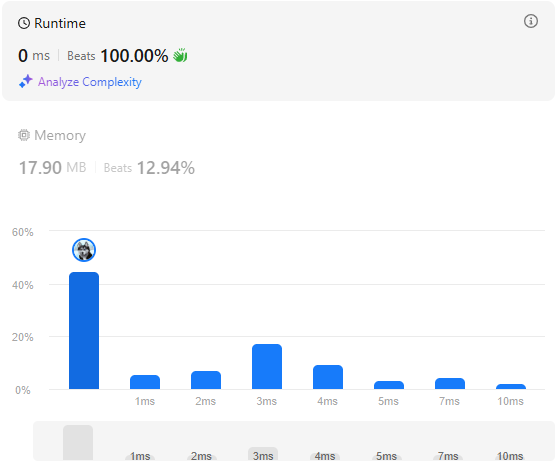

4. 결론

처음에는 gcd를 누적하지 않아서 애를 먹었지만 누적하며 찾아가니 쉽게 풀 수 있었다.