1. 문제 소개

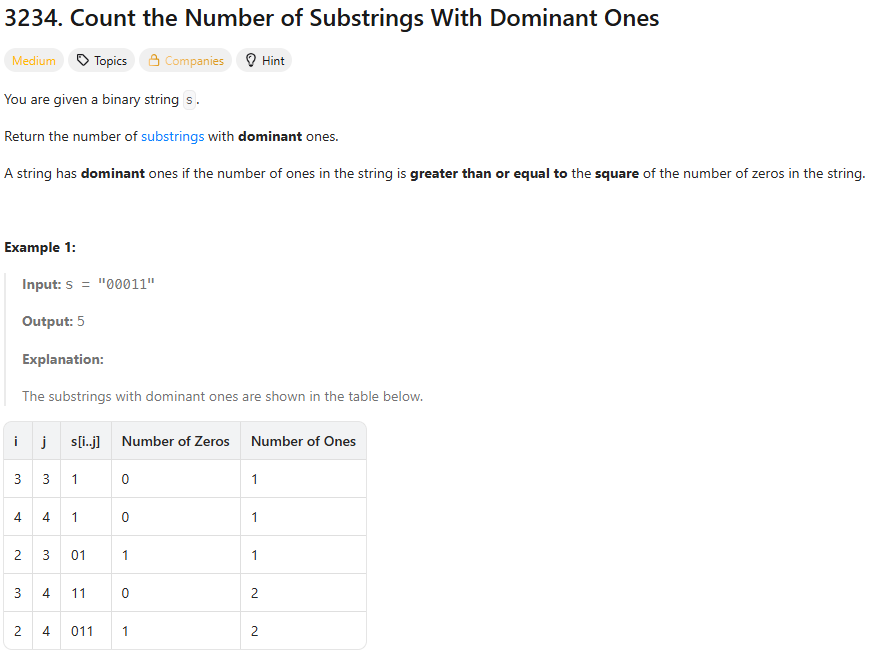
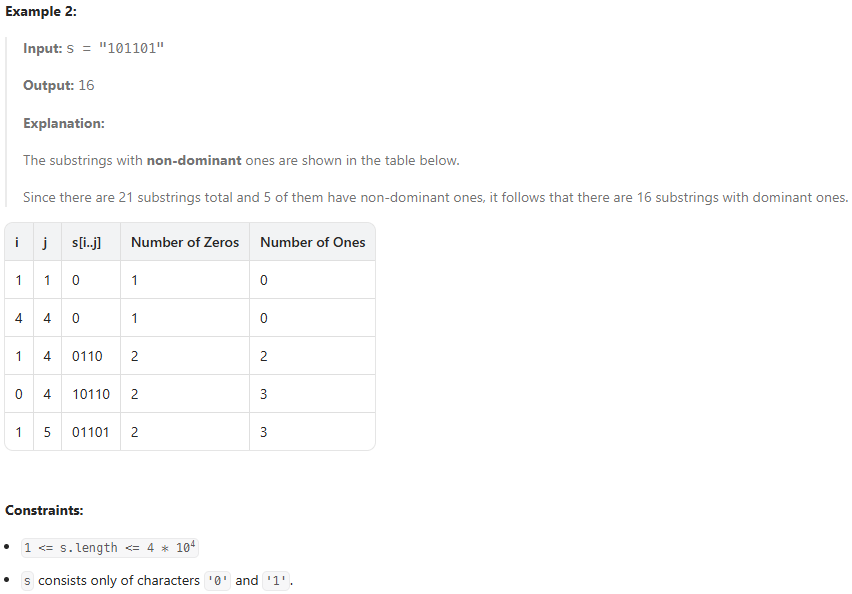
3234. Count the Number of Substrings With Dominant Ones

2. 나의 풀이

주말이라 그런지 혼자 힘으로 풀지 못했다.

3. 다른 풀이

풀이는 아래와 같은데 아직 잘 이해되지 않아서 공부가 필요하다.

class Solution:
    def numberOfSubstrings(self, s: str) -> int:
        n = len(s)                            # 문자열 길이 n
        pre = [-1] * (n + 1)                  # pre[i]: 위치 i-1 기준으로, 직전(왼쪽) 0의 인덱스를 저장하는 배열

        for i in range(n):                    # 0 ~ n-1까지 순회하며 pre 배열 채우기
            if i == 0 or s[i - 1] == "0":     # i==0 이거나, 바로 앞 문자가 '0'이면
                pre[i + 1] = i                # 직전 0의 위치는 현재 인덱스 i
            else:                             # 앞 문자가 '1'이면, 직전 0 위치는 그대로 이어받음
                pre[i + 1] = pre[i]

        res = 0                               # 조건을 만족하는 부분문자열 개수
        for i in range(1, n + 1):             # 부분문자열의 끝 인덱스를 i-1로 고정 (1-based처럼 사용)
            cnt0 = 1 if s[i - 1] == "0" else 0  # 끝 문자가 '0'인지에 따라 0의 개수 초기화
            j = i                             # j: 시작 후보들을 역방향으로 따라갈 포인터 (pre를 통해 점프)
            while j > 0 and cnt0 * cnt0 <= n: # j가 범위 내이고, cnt0^2가 n을 넘지 않을 때만 진행 (상한 가지치기)
                cnt1 = (i - pre[j]) - cnt0    # 구간 [pre[j], i) 안의 길이에서 0 개수를 빼서 1 개수 계산
                                              #   길이 = i - pre[j]
                                              #   그 중 0은 cnt0개 → 1은 나머지
                if cnt0 * cnt0 <= cnt1:       # 조건 cnt1 >= cnt0^2 가 만족되면
                    res += min(               # 이 구간에서 유효한 시작점 개수를 한 번에 더함
                        j - pre[j],           #   (j ~ pre[j]+1 사이의 시작점 후보 개수)
                        cnt1 - cnt0 * cnt0 + 1#   (1 개수가 조건을 만족하는 최대 시작점 개수)
                    )
                j = pre[j]                    # j를 "직전 0의 위치+1" 부근으로 점프(다음 시작 후보 그룹으로 이동)
                cnt0 += 1                     # 한 단계 이동할 때마다 0을 하나 더 포함하는 케이스로 확장

        return res                            # 모든 끝점 i에 대해 누적한 dominant 부분문자열 개수 반환

4. 결론

더 노력하자.