1. 문제 소개

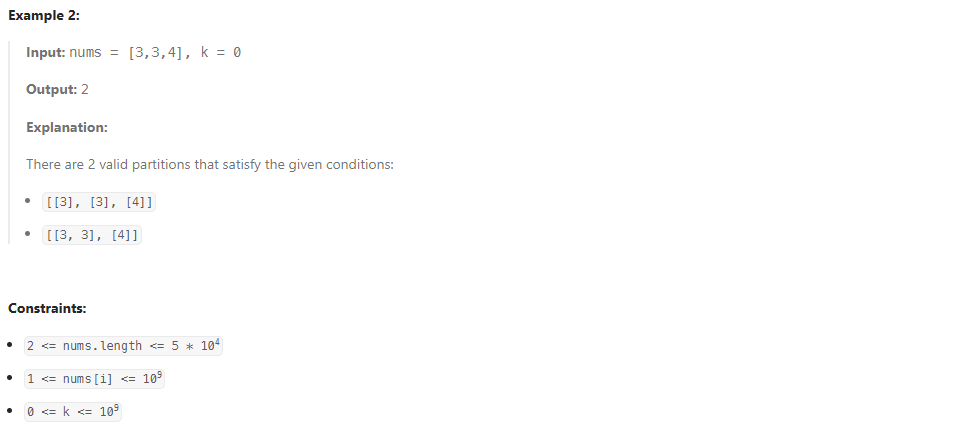
3578. Count Partitions With Max-Min Difference at Most K

2. 나의 풀이

dp와 sliding window가 힌트로 주어졌다.
너무 오랫만이라 공부를 하며 풀었다.
문제를 보면 배열을 순회할 때, 최댓값과 최솟값의 차가 k보다 큰 경우를 나눠야 한다.
그러나 바로 생각이 들지 않았고, 설명을 봐가며 풀었다.
이 경우 시간복잡도는 $O(n\, log n)$이다.

class Solution:
    def countPartitions(self, nums: List[int], k: int) -> int:
        MOD = 10**9 + 7           # 나머지 연산에 사용할 모듈러
        n = len(nums)             # 배열 길이

        dp = [0] * (n+1)          # dp[i] = nums[0..i-1]을 조건에 맞게 분할하는 방법 수
        dp[0] = 1                 # 빈 prefix를 분할하는 방법은 1가지(아무 것도 안 나누는 것)

        prefix = [0] * (n+1)      # prefix[i] = dp[0] + dp[1] + ... + dp[i] (dp의 prefix sum)
        prefix[0] = 1             # prefix[0] = dp[0]

        cnt = SortedList()        # 현재 윈도우 [j..i] 구간의 값들을 정렬 상태로 유지하는 구조

        j = 0                     # 투 포인터 왼쪽 인덱스(현재 윈도우의 시작점)
        for i in range(n):        # i: 현재 고려 중인 subarray의 끝 인덱스
            cnt.add(nums[i])      # 윈도우에 nums[i] 포함 (정렬 상태 유지)

            # 현재 윈도우 [j..i]에서 max-min > k 이면, 조건을 만족할 때까지 j를 오른쪽으로 이동
            while j <= i and cnt[-1] - cnt[0] > k:
                cnt.remove(nums[j])  # 왼쪽 끝 값을 윈도우에서 제거
                j += 1               # 윈도우 시작점 자리를 한 칸 오른쪽으로 이동

            # 이제 [j..i]는 (max-min) ≤ k 를 만족하는 **최대**의 구간이 되어 있음.
            # 끝이 i인 마지막 subarray의 시작점 t는 j ≤ t ≤ i 이고,
            # 각 t에 대해 "prefix t까지의 분할 방법(dp[t]) + 마지막 구간[t..i]" 조합이 가능.
            # 따라서 dp[i+1] = sum(dp[t]) for t in [j..i]
            # → prefix sum을 이용해 구간 합 계산:
            #   sum(dp[j..i]) = prefix[i] - prefix[j-1] (j > 0일 때),
            #   j == 0 이면 prefix[i] 전체를 쓰면 된다.
            dp[i+1] = (prefix[i] - (prefix[j-1] if j > 0 else 0)) % MOD

            # prefix[i+1] 업데이트: prefix[i+1] = prefix[i] + dp[i+1]
            prefix[i+1] = (prefix[i] + dp[i+1]) % MOD

        return dp[n]              # 전체 배열(nums[0..n-1])을 분할하는 방법 수 반환

3. 다른 풀이

queue를 이용한 다른 방봅도 존재한다.
이 경우 시간복잡도는 $O(n)$이다.

class Solution:
    def countPartitions(self, nums: List[int], k: int) -> int:
        n = len(nums)
        mod = 10**9 + 7

        dp = [0] * (n + 1)            # dp[i]: nums[0..i-1]까지 조건을 만족하며 분할하는 방법 수
        prefix = [0] * (n + 1)        # prefix[i] = dp[0] + ... + dp[i] (구간 합 계산용)

        min_q = deque()               # 현재 윈도우 내 최소값을 관리하는 monotonic 증가 deque
        max_q = deque()               # 현재 윈도우 내 최대값을 관리하는 monotonic 감소 deque

        dp[0] = 1                     # 빈 배열을 분할하는 경우의 수는 1
        prefix[0] = 1

        j = 0                         # 투 포인터 윈도우 시작점

        for i in range(n):            # i: 구간의 끝 지점

            # --- 최대값 유지(max deque) ---
            # nums[i]보다 작거나 같은 값은 pop → 감소하는 형태 유지
            while max_q and nums[max_q[-1]] <= nums[i]:
                max_q.pop()
            max_q.append(i)

            # --- 최소값 유지(min deque) ---
            # nums[i]보다 크거나 같은 값은 pop → 증가하는 형태 유지
            while min_q and nums[min_q[-1]] >= nums[i]:
                min_q.pop()
            min_q.append(i)

            # --- 윈도우 조정: max-min > k이면 왼쪽 j를 당긴다 ---
            while max_q and min_q and nums[max_q[0]] - nums[min_q[0]] > k:
                # j가 윈도우 밖으로 나가면 deque에서 제거
                if max_q[0] == j:
                    max_q.popleft()
                if min_q[0] == j:
                    min_q.popleft()
                j += 1

            # --- dp 계산 ---
            # dp[i+1] = sum(dp[t]) for t in [j..i]
            if j > 0:
                dp[i + 1] = (prefix[i] - prefix[j - 1] + mod) % mod
            else:
                dp[i + 1] = prefix[i] % mod

            # prefix sum 업데이트
            prefix[i + 1] = (prefix[i] + dp[i + 1]) % mod

        return dp[n]

4. 마무리

dp와 sliding window 공부가 필요하다.