1. 문제 소개

778. Swim in Rising Water

2. 나의 풀이법

보자마자 bfs가 떠올랐다. 문제는 $t$에 따라서 어떻게 효율적으로 알고리즘을 조정하는 것이다. 감이 잘 안잡혀 조금 검색하며 풀어보았다.

import heapq as hq

class Solution:
    def swimInWater(self, grid: List[List[int]]) -> int:
        n = len(grid)
        visited = [[False] * n for _ in range(n)]
        dirs = [(1,0), (0,1), (-1,0), (0,-1)]

        q = [(grid[0][0], 0, 0)]
        visited[0][0] = True

        while q:
            h, x, y = hq.heappop(q)
            if x == n-1 and y == n-1:
                return h

            for dx, dy in dirs:
                nx, ny = x + dx, y + dy
                if 0 <= nx < n and 0 <= ny < n and not visited[nx][ny]:
                    visited[nx][ny] = True
                    nh = max(h, grid[nx][ny])
                    hq.heappush(q, (nh, nx, ny))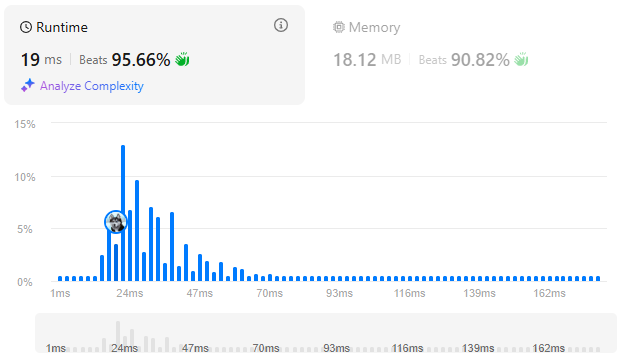

꽤나 좋은 성적을 냈다.
이전 문제와 비슷하게 풀었는데 말이다.
기분이 좋다.
이 경우 시간복잡도는 $O(n^2\, log\, n)$이고 공간복잡도는 $O(n²)$이다.

3. 다른 풀이법

class Solution:
    def swimInWater(self, grid: List[List[int]]) -> int:
        m, n = len(grid), len(grid[0])
        
        def possible(mid):
            seen = set()
            
            def dfs(r, c):
                if r == m-1 and c == n-1:
                    return True
                seen.add((r, c))
                for dr, dc in [(0, 1), (1, 0), (0, -1), (-1, 0)]:
                    nr, nc = r + dr, c + dc
                    if 0 <= nr < m and 0 <= nc < n and (nr, nc) not in seen:
                        if grid[nr][nc] <= mid:
                            if dfs(nr, nc):
                                return True
                return False
            
            return grid[0][0] <= mid and dfs(0, 0)
        
        def binary_search():
            lo, hi = grid[0][0], max(max(row) for row in grid)
            while lo < hi:
                mid = (lo + hi) // 2
                if possible(mid):
                    hi = mid
                else:
                    lo = mid + 1
            return lo
        
        return binary_search()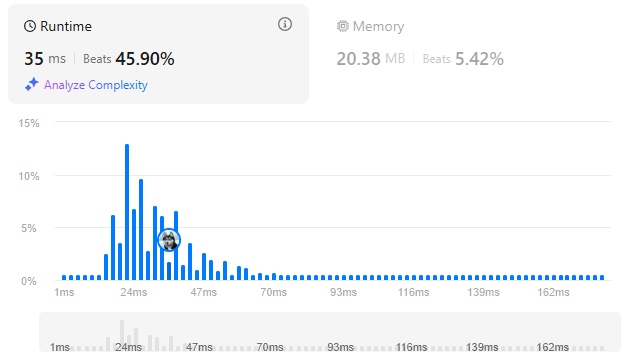

이 풀이법의 경우 binary search와 dfs를 사용했다.
이 경우도 시간복잡도는 $O(n^2\, log\, n)$이고 공간복잡도는 $O(n²)$이다.

4. 결론

지금까지는 bfs를 이용한 풀이가 마음에 들어서 이를 반복했다. 구현도 재귀를 사용하는 dfs보다 쉽기 때문일 것이다.
둘 모두 잘 사용해서 풀어야겠다.