https://www.youtube.com/watch?v=T9l891a0f3o
# include <stdio.h>
int main(void)
{
float y = 123456789.123456789;
printf("실수 %.15f의 크기는 %d \n", y, sizeof(y));
return 0;
}
출력이 이상하다. float의 범위가 -3.4 x 10^-37 ~ 3.4 x 10^38 라면서 정확한 값이 출력되지 않는다. 그 이유를 알아보자.
float의 저장 방식
IEEE 754 standard에 따라 값을 저장한다. 링크

float은 값을 2진수로 표현한 후, 부호, 지수, 유효숫자로 나눠서 4byte 메모리에 저장한다.
우선 10진수 소수형을 2진수 소수형으로 표현하는 방법을 알아보자.
6.5 -> 110.
0.5에 2를 곱해주면 정수부분에 올라가는게 있으므로 1을 적어준다.
소수점 값이 0이 되었으므로 계산이 종료된다.
따라서 소수점 표현은 110.1
6.4 -> 110.
0.4에 2를 곱해주면 정수부분에 올라가는게 없으므로 0을 적어주고,
0.8에 2를 곱해주면 정수부분에 올라가는게 있으므로 1을 적어주고,
0.6에 2를 곱해주면 정수부분에 올라가는게 있으므로 1을 적어주고,
0.2에 2를 곱해주면 정수부분에 올라가는게 없으므로 0을 적어주고,
0.4에 2를 곱해주면 정수부분에 올라가는게 없으므로 0을 적어주고,
... 반복
위에서 아래로 쭉 적어보면 011001100110110... 으로 끝나지 않는다.
따라서 소수점 표현은 110.0110110110110...2를 곱해주면서 자릿수 올림이 일어나면 1을 적어주고, 아니면 0을 적어주면서 확인할 수 있다.
이렇게 6.5는 유효숫자 부분이 딱 떨어지지만, 6.4는 그렇지 않고, 많은 경우 소수부분이 이렇게 딱 떨어지지 않는다. 소수 부분이 정확하게 떨어지지 않는 경우 유효숫자가 매우 길어지고, 유효숫자를 메모리에 저장할 때 뒷부분이 잘리게 된다. 그래서 오차가 발생하고, 이러한 실수의 오차를 입실론 오차라고 부른다.
다음으로, 4byte 메모리에 저장하는 방식을 알아보자.
부호: 1비트
지수부: 8비트
가수부: 나머지
예를 들어 1100001.011001 이라는 이진수 값이 있다고 할 때, 1.10000011001 * 2^6 으로 표현 가능하며, 여기서 부호는 +, 지수는 6, 가수는 10000011001 이다.
-
부호가 +면 부호 비트는 0, -면 부호 비트는 1이다.
-
지수부는 8비트이므로 -127부터 127까지 표현이 가능한데, 부호 비트를 따로 두지 않고 bias를 127만큼 줘서, 00000000 은 -127, 11111111은 127로 표현한다. 따라서 만약 지수가 -127이라면 127을 더해서 0이 되고, 지수가 6이라면 127을 더해서 133이 되며, 이 더한 값을 이진수로 표현하여 넣는다.
6이라면 00000110 이 아니라 10000101을 넣어줘야 한다
-
가수부는 왼쪽부터 순서대로 적어준다. 예의 경우 10000011001000000000000 을 적어준다.
23비트의 십진수 정수 범위는 2^23 = 8,388,608로,
비트가 3개면 2^3 - 1 까지 표현 가능
비트가 4개면 2^4 - 1 까지 표현 가능
...
비트가 23개면 2^23 -1 까지 표현 가능하므로 약 800만 정도, 즉 float의 경우 십진수 표현시 유효 숫자의 범위가 소수점 이하 6자리까지는 정확하고, 7자리부터는 부정확할 수 있다(큰 값은 부정확)는 것을 알 수 있다.
위 이야기는 1.1234567 같이 표현하려는 값의 정수부가 한 자리인 경우에 해당하고, 정수부가 더 길어지면 그만큼 표현할 수 있는 소수점 이하 자리도 작아지게 된다.
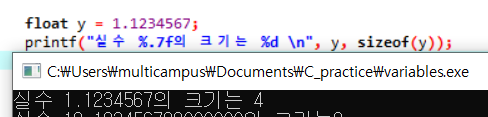
소수점 이하 7자리까지 잘 표현됨

소수점 이하 6자리까지 정확하다.
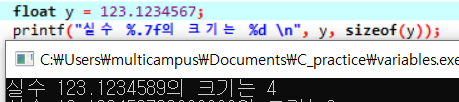
소수점 이하 5자리까지 정확하다.
헷갈리는 포인트 정리
https://docs.microsoft.com/en-us/cpp/c-language/type-float?view=msvc-160
float이 따르는 IEEE754 single precision 32bit의 경우 지수부 8비트, bias 127로 설정되어 있다. 위에서는 대충 설명했지만 좀 더 자세히 알아보며 정확한! float의 범위를 알아보자.
- 8비트의 경우 0 ~ 255의 숫자를 표현할 수 있다. (256개 숫자)
- bias가 127로 설정된 이유는 다음과 같다.
- 0은 underflow를 처리하고, 255는 overflow를 처리하는데에 사용하여 남은 표현 가능 수가 1부터 254까지의 254개이기 때문에 정확히 중간 값인 127을 bias로 한 것이다.
- 여기서 말한 0은 00000000, 255는 11111111 비트를 말한다.
- 따라서 0과 255를 제외하고, 127을 중간 지점으로 잡으면
- 1은 -126
- 127은 0
- 254는 127
- 표현 가능한 이진수 지수 범위는 -126 ~ 127 이다.
- 2^-126 = 1.17 * 10^-38
- 2^127 = 1.7 * 10^38
이렇게 지수 범위를 알게 되었다. 이제 가수 부분을 생각해보면,
2진수 숫자 1010101 이 있고, 가수부 메모리가 6비트라고 가정할 때(원래 23비트인데 0101010000000...처럼 다 쓰기 뭐해서..)
- 1.010101 * 2^6 으로 정규화하여 표현 가능하다.
- 이때 메모리의 가수 부분에는 010101을 넣게 된다. (맨 앞의 1은 당연하므로 메모리에 넣지 않는다)
- 이 경우 가수부에 들어갈 수 있는 값의 범위는 000000 에서 111111로, 그럴 리는 없겠지만 111111을 넘어가면 1.1000000 * 2^7 과 같을 것이다.
- 생략된 맨 앞의 1을 포함하면 아래와 같이 생각할 수 있다.
- 가수부 000000은 실제로는 1.000000로, float값이 1.0일 때이다.
- 가수부 111111은 실제로는 1.111111로, float값에 2가 곱해지기 직전이다.
즉, 특정 지수값이 있을 때 가수부에 의해 정확한 값을 계산하게 되며, 가수부의 범위는 1 ~ 2 로 생각할 수 있다.
따라서 float으로 표현 가능한 값의 범위를 구해보면,
지수가 127일 때 가수의 범위가 1 ~ 2라면
최소 1 * 2^127, 최대 2 * 2^127 값을 표현할 수 있고,
이때 최대값은 약 3.4 * 10^38 이다.
부호 비트에 따라 부호가 바뀌므로 결국 float으로 표현할 수 있는 값의 범위는
-3.4 * 10^38 ~ 3.4*10^38 이 맞다.
표현할 수 있는 가장 작은 소수점 이하 값은 지수가 -126일 때 약 1.17 * 10^-38 이고, (0.000...000117 같은 값을 말함)
float값의 범위가 1.17 10^-38 ~ 3.410^38 인 것은 아니라는 점에 주의하자.
돌아보기
c언어 float 출력을 공부하다가 여기까지 왔다. float의 출력이 이상하다고만 생각했는데 이상한게 아니라 당연한 것이었고, 이론상으로 저장 가능한 float의 범위와 실제 정확하게 사용 가능한 float값의 범위가 다르다는 것이 크게 다가왔다.