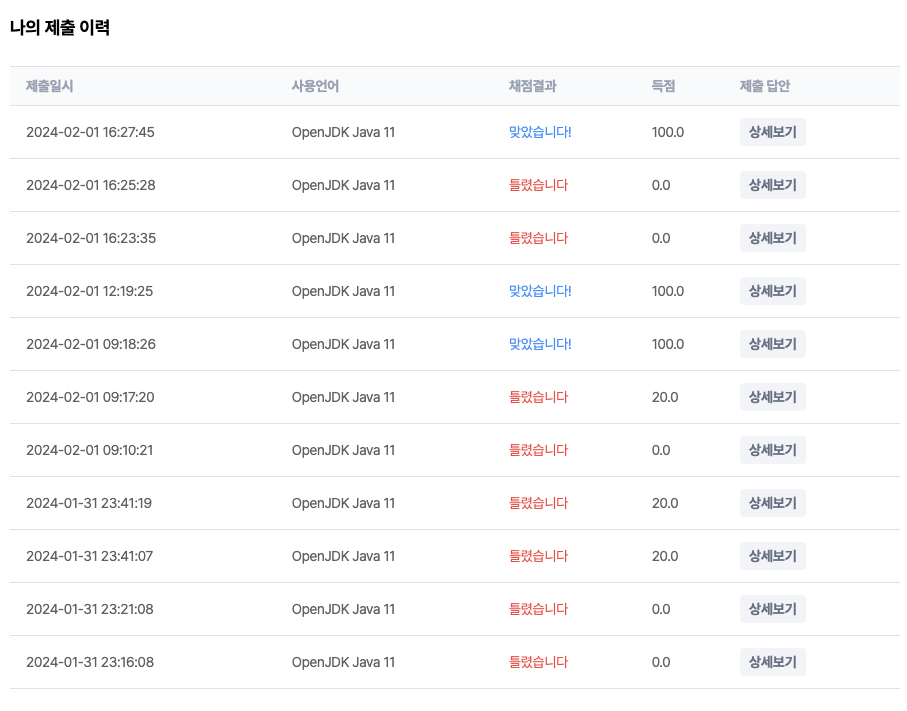
통근버스 출발 순서 검증하기

링크: https://softeer.ai/practice/6257
문제분류 : DP(메모이제이션)
난이도 : Level 3
풀이시간 : 초과 -> 정답확인
결과: 실패
공식해설(코드없음): https://softeer.ai/class/lecture/84

회고

처음 풀 때는 순열인줄 알고 순열로 풀고 테스트 케이스를 확인했다.
근데 순열로 풀었을 때도 잘못된 부분이 있어서 테스트 케이스 4개 중에 2개만 맞았었다.
고치고 나서 제출해서 확인해보니, 틀렸었다...!
다른 풀이를 고민하다 잘 모르겠어서 결국 답을 확인했다.
순열로 푸는 방식(완전탐색)은 대표적인 오답이었다.
생각해보니 N이 5000까지여서 N^3이면 어마어마한 시간 복잡도가 나온다;;

결국 이 문제를 풀려면 N^3보다 작은 시간 복잡도를 가진 알고리즘이어야 한다.
풀이를 보니 2차원 배열에 비교 후보들을 적어놓고 O(N^2)으로 조건 비교하는 방식이었다.
2차원 배열을 가지고 답을 구하는 방식이 이해가 안가서 거의 5번도 넘게 해답을 보면서 공부했다...

꼭 풀고야 말겠다는 제 불굴의 의지가 보이시나요? ㅋ.ㅋ

다른 블로그에는 이 문제를 부분합 문제라고 분류하는데,
난 이 문제가 부분합이라는게 공감(?)이 안돼서 내 마음대로 문제를 분류했다.
2차원 배열에 적어놓고 답 구하니까 메모이제이션 아닌가...? 흠

푸는 방법을 이해하고 풀이를 안보고 다시 풀었는데도
특정 부분에서 구현을 잘 못해서 굉장히 애먹었다.

이번 회고에서는 내가 문제풀이를 이해하는 과정과
코드 작성 중 틀리는 부분을 중점적으로 써보려고 한다.

내 코드

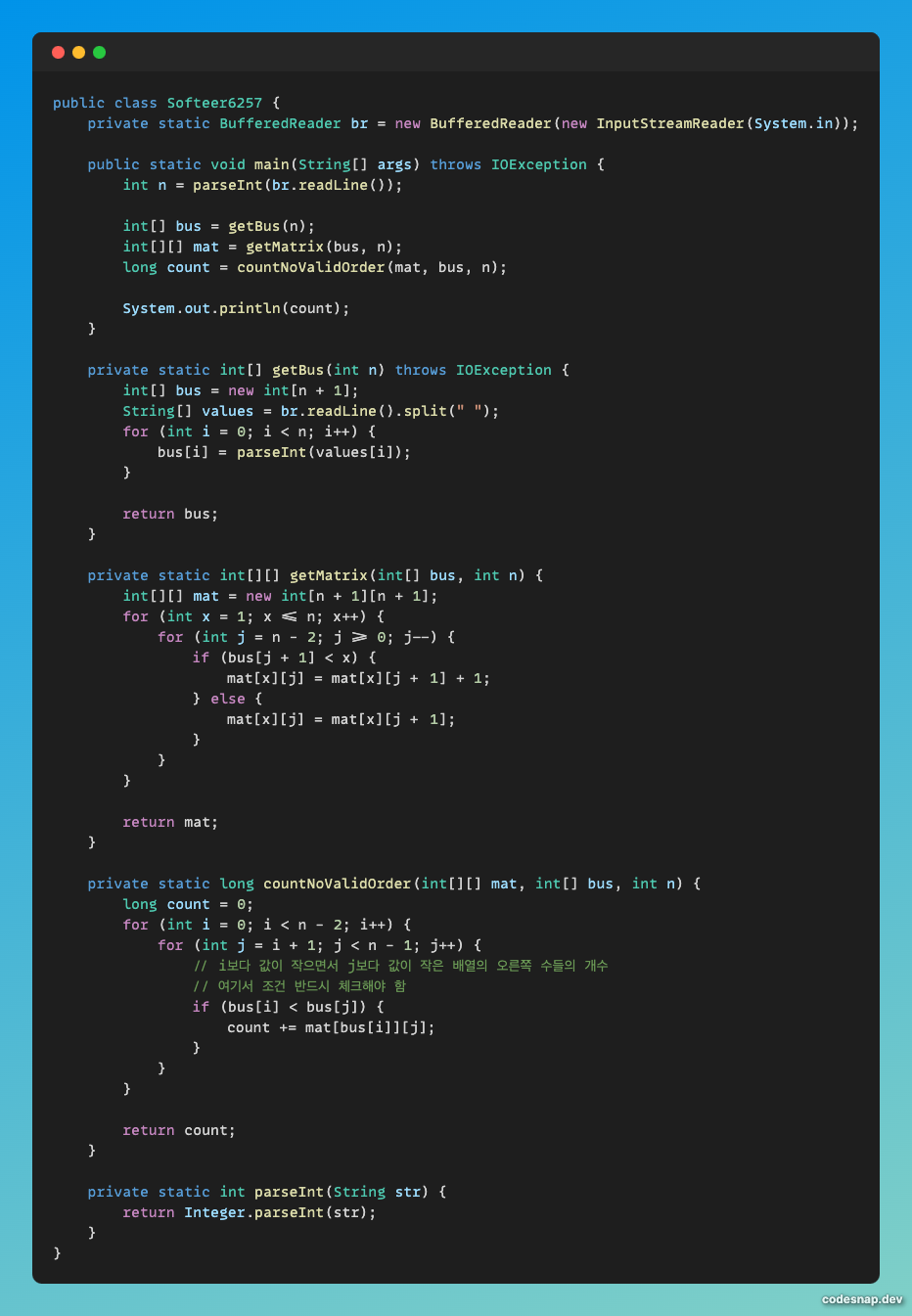
단순히 값을 받는 부분은 생략하도록 하겠다.
이 문제에서 핵심이 되는 부분은 getMatrix와 countNoValidOrder이다.

먼저 이 문제에서 스택정렬이 안되는 경우를 생각해보자.
아래의 세가지 조건을 모두 만족할 때이다.

1) i < j < k
2) ai < aj
3) ak < ai

시간복잡도가 낮으면서 이 세 조건을 쉽게 검증할 수 있어야 한다.

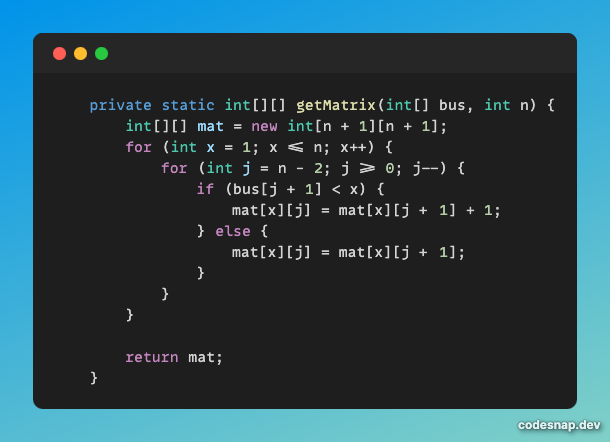
검증을 위한 방법으로 2차원 배열을 만든다.
행의 인덱스인 x와 열의 인덱스인 j에는 1부터 n까지의 숫자가 온다.

2차원 배열에 저장하는 값은 1차원 배열인 bus에서
j번째 인덱스 이후에 값들 중 x의 값보다 작은 값의 개수를 저장한다.
이게 핵심 아이디어인데, 처음 해설을 보면 이 부분을 이해하기가 꽤 어렵다.

이 개수를 저장하는 이유는 ak < ai 조건을 체크하기 위함이다.

더 자세한건 countNoValidOrder에서 다시 설명해보겠다.

getMatrix의 이중 for문에서 j의 값이 역순으로 진행된다.
왜냐하면 역순으로 진행하면서 얻을 수 있는 장점이 있기 때문이다.

만일 j번째 인덱스 이후에 값들 중 x의 값보다 작은 값이 있다면,
현재 위치보다 이전에 저장한 개수보다 1개 더 많아지기 때문이다.
이 부분을 의미하는 코드가 if (bus[j + 1] < x) 이다.
그리고 이 조건에 맞지 않으면 이전에 저장해놓은 개수를 그대로 가져와 현재 위치에 저장하면 된다.
물론 j를 역순으로 진행 안해도 상관은 없다!

이렇게 만든 matrix 배열을 가지고 countNoValidOrder에서 답을 찾는다.

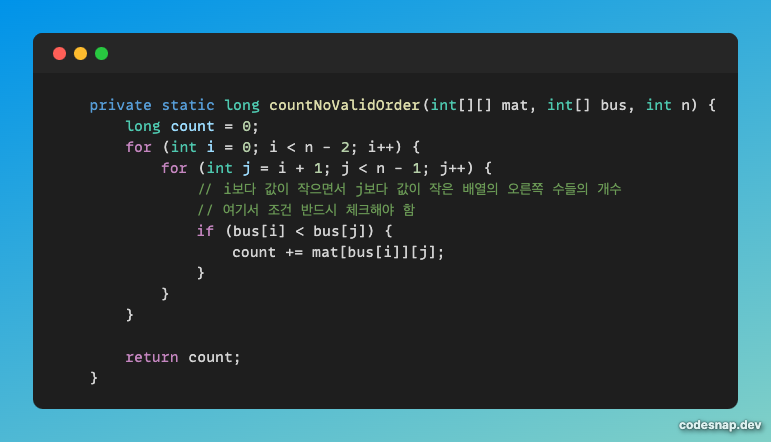
이 코드를 주목하자.

이중 for문에서 i와 j의 조건이 1) i < j 조건을 만족시키고 있다.
그리고 안쪽에 if (bus[i] < bus[j])에서 2) ai < aj 조건을 만족시키고 있다.

그러면 이제 남은 조건은 j < k, ak < ai 이다. 이 조건은 어떻게 찾을 수 있을까?
아까 만들어준 2차원 배열인 matrix로 가능하다. 그 이유는 다음과 같다.

matrix[x][j]에 들어가는 값은 x보다 작은 j 이후의 값의 개수이다.
x <= bus[i] 로 하고, matrix[bus[i]][j]에서
j 이후의 bus[i] 보다 작은 값을 ak라고 잡아주면 된다.

사실 내가 썼는데도 설명이 복잡하다...!
나중에 기회가 된다면 그림으로 그려서 추가 설명을 해보도록 하겠다.

어쨋든! 1), 2), 3)의 모든 조건을 2차원 배열을 돌면서 찾으면 되기 때문에,
답을 O(N^3)보다 작은 O(N^2) 수준에서 찾을 수 있다.

내가 구현하면서 가장 실수를 많이 했던 부분은 반복문의 인덱스를 설정하는 부분이다.

1) 배열의 인덱스를 0부터 시작할지, 1부터 시작할지 설정
2) getMatrix 메서드에서 인덱스 j가 역순으로 돌때, 시작 인덱스와 끝 인덱스 설정

자칫 잘못해서 0부터 시작해야하는데, 1부터 시작한다든지
혹은 반대로 한다든지 섞여버리면 답이 절대 안나오기 때문이다... ㅠㅠ
이 부분은 그냥 본인만의 규칙을 잘 만들어서 계속 연습하는게 좋은거 같다.

나는 직관적으로 이해하려고 인덱스를 1부터 시작하는 편이다...!
근데 오랜만에 알고리즘 풀면 이 방식을 뒤섞어서 실수가 나온다.
꾸준히 연습하자...