Problem Description
There are n cities connected by some number of flights. You are given an array flights where flights[i] = [fromi, toi, pricei] indicates that there is a flight from city fromi to city toi with cost pricei.
You are also given three integers src, dst, and k, return the cheapest price from src to dst with at most k stops. If there is no such route, return -1.
Examples
Example 1:
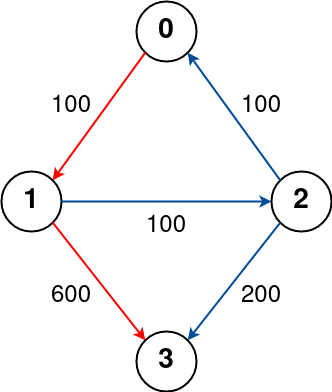
Input:
n = 4, flights = [[0,1,100],[1,2,100],[2,0,100],[1,3,600],[2,3,200]], src = 0, dst = 3, k = 1
Output:700
Explanation:
The graph is shown above.
The optimal path with at most 1 stop from city 0 to 3 is marked in red and has cost 100 + 600 = 700.
Note that the path through cities [0,1,2,3] is cheaper but is invalid because it uses 2 stops.
Example 2:
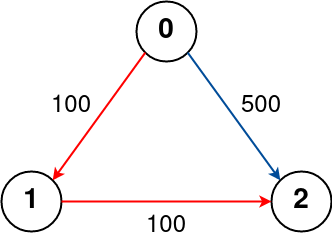
Input:
n = 3, flights = [[0,1,100],[1,2,100],[0,2,500]], src = 0, dst = 2, k = 1
Output:200
Explanation:
The graph is shown above.
The optimal path with at most 1 stop from city 0 to 2 is marked in red and has cost 100 + 100 = 200.
Approach
The problem is a common example of dijkstra's algorithm (to be discussed separately). We want to go through each neighbor, starting from the starting node (src), until we reach (dst), or the endpoint.
A priority queue is used to select the node that currently has the lowest price. Then, we will only traverse an edge to a node x if x has not already been visited with fewer stops. Because we are greedily choosing the node with the lowest total price, the first time we reach dst, we will have the answer.
Solution
class Solution:
def findCheapestPrice(self, n: int, flights: List[List[int]], src: int, dst: int, k: int) -> int:
graph = defaultdict(list)
for x, y, z in flights:
graph[x].append([y, z])
distances = [inf] * (n + 1)
distances[src] = 0
q = deque([(0, src, 0)])
while q:
curr_dist, node, curr_cnt = q.popleft()
if curr_cnt > k:
continue
for nei, weight in graph[node]:
dist = curr_dist + weight
if dist < distances[nei]:
distances[nei] = dist
q.append((distances[nei], nei, curr_cnt + 1))
return distances[dst] if distances[dst] < inf else -1