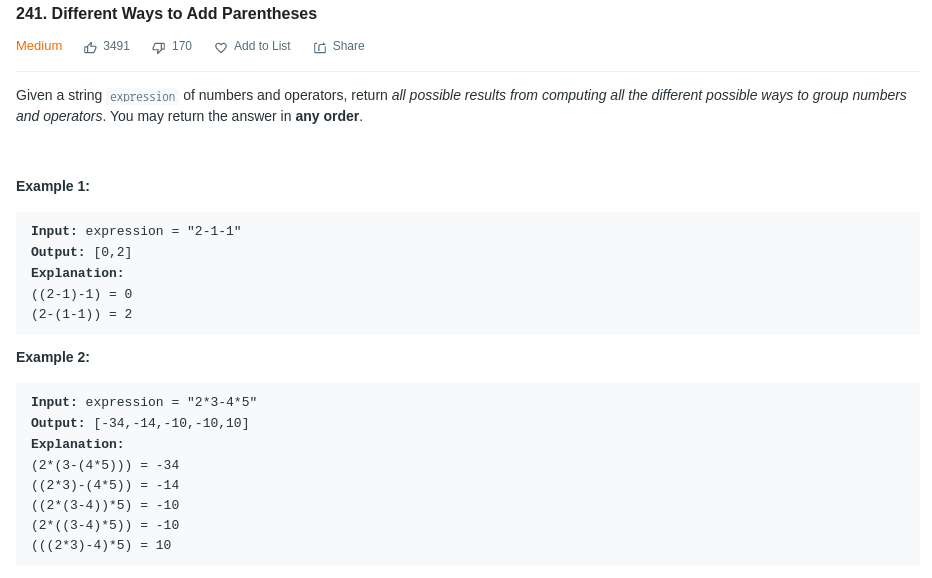
개인적으로 많이 어렵고 이해하기 힘들다고 생각했다. 요즘들어 코딩에 있어서 많이 슬럼프가 오는 이유 중 하나도 이 유형의 문제 때문인거 같다. 다이나믹 프로그래밍에 있어서 더 배우고 싶은데 이해는 잘 안되고 내가 풀고싶은데로 잘 안풀리다 보니깐 점점 뇌가 생각하는걸 멈추는 기분이라 너무 슬펐다. 탈출구부터 찾을려는 내 모습이 솔직히 마음에 안들고 더 노력해야겠다는 생각이 들었다.
먼저 이 문제는 generate parentheses 같은 유형의 문제 같았다. 어떤 특정 조건에서 backtracking 을 두번하고 리턴되는 값으로 계산 하는게 핵심인데 재귀 과정을 생각하는 단계에서 많이 헷갈려서 이곳저곳 답도 그렇고 영상도 그렇고 많이 참고했었다.
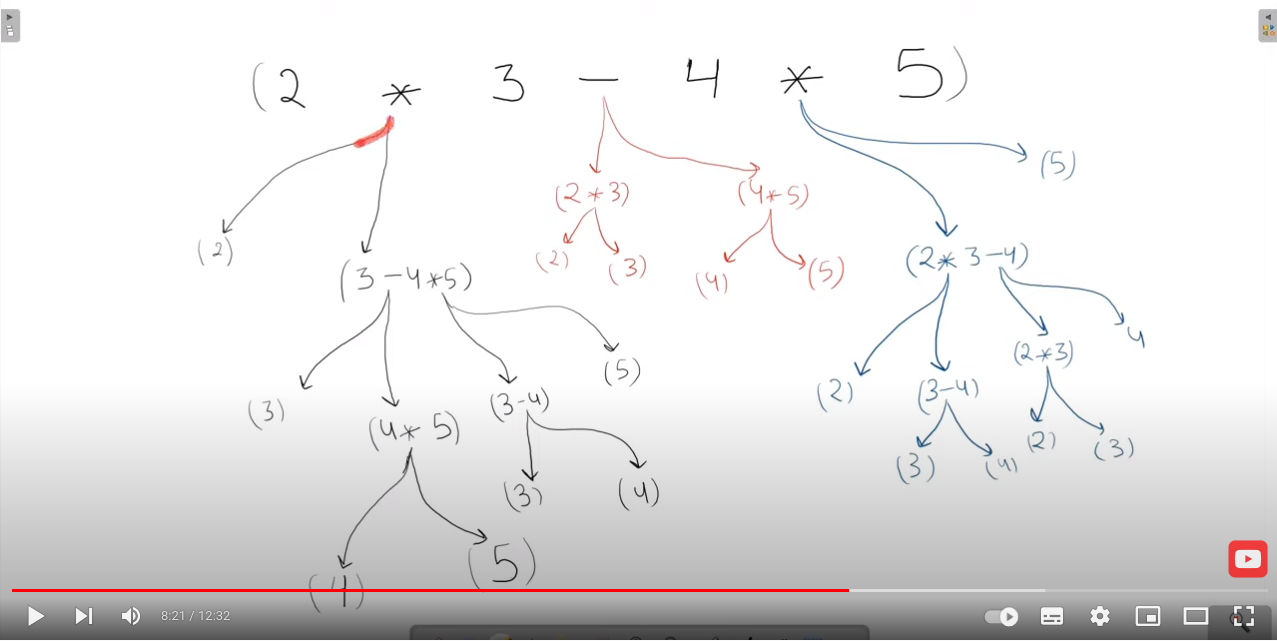
기본적인 과정은 영상에 나온 설명과 같이 부호 (expression) 이 나오게되면 substr을 이용해서 자른 후에 숫자만 남을때까지 재귀를 하고 해당 expression 에 따라서 결과를 result 벡터에 저장해두면 마지막 재귀 시작 룹에 왔을때 모든 계산이 끝난다.

그냥 재귀 형식으로만 문제를 풀면 이렇다. 해당 재귀 함수에 result 가 빈다는 뜻은 곧 부호가 없다는 뜻이므로 숫자를 변형해서 넣어준다음에 left 와 right 에 있는 함수를 비교하면서 계산해주면서 올라가면 된다.

그러나 날 괴롭히고 있는 DP 방식의 Top-down Memorization 방식을 이용하면 코드가 정말로 빨라진다는걸 알수가 있는데 너무 신기했다. 구종만 책에서 배운 방식을 조금 변형한 형태지만 확실히 그저 result를 리턴하는 형태가 아니고 dp 테이블에 result를 저장해둔 뒤에 만약 존재한다면 바로 리턴하는것만으로도 엄청나게 향상된 알고리즘을 확인 할수있어서 새로운 방식이었다. 다시한번 써봐야겠다.
배운점:
1. 책에서 배운 Memorization 에 활용법
2. Backtracking 연습
