Jump Game II (Java, C++)

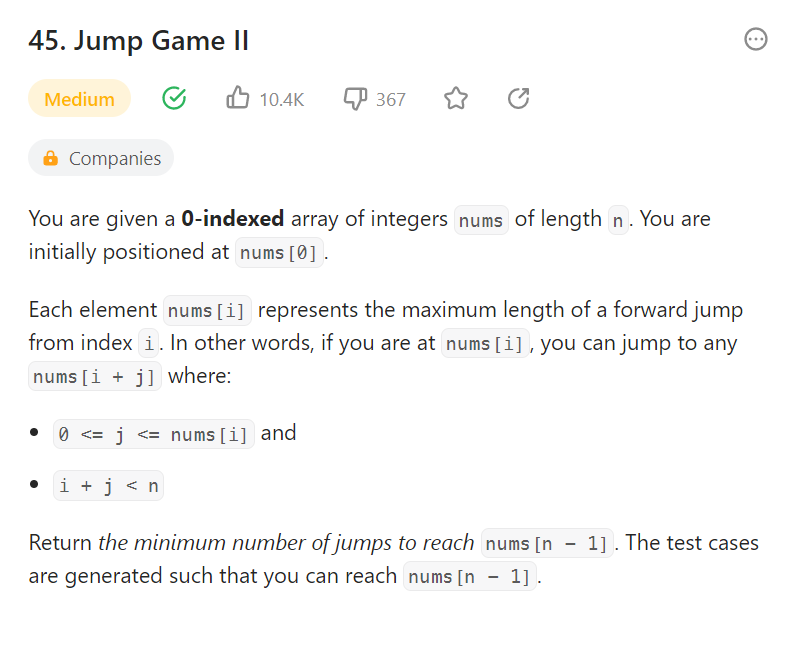
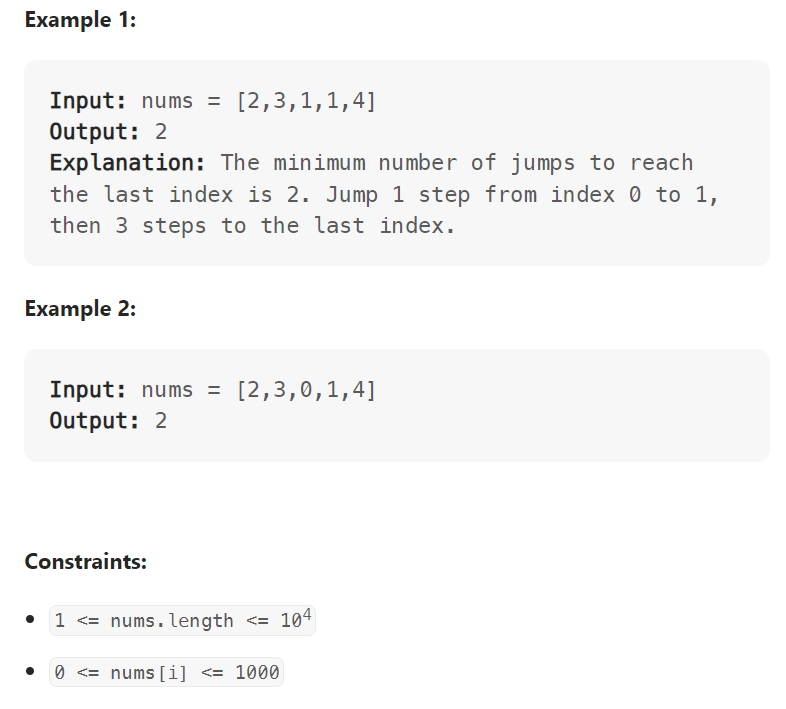
추억이 있는 문제다. 첫번째 시리즈의 목적이 해당 index에 도달이 가능한지에 대한 여부를 묻는 문제였다면 이번 문제는 해당 index에 도달이 가능한 가장 최소한의 점프를 물어보는 문제다.

이 문제를 생각할때 고민이 많이 들었는데 뭔가 엄청 DP로 최적화 하는 느낌은 안들었다. 결국 완전탐색을 해야하는 구조가 불편했지만 여기서 더 최적화 하는 방법은 내가 아는것보다 좀 더 나아가야만 했었다. 일단 솔루션은 가장 첫번쨰 index는 우리가 시작하는 위치이기 떄문에 최소가 항상 0이다.

그 다음부터는 이중 룹으로 내가 점프할 수 있는 구간만큼 점프한 다음에 그 구간이 가진 현재의 값과 내 위치에서 점프했을때 +1한 값을 비교하면서 마지막에 최소 값을 리턴하면 끝난다.

class Solution {
    public int jump(int[] nums) {
        int[] dp = new int[nums.length]; 
        Arrays.fill(dp,Integer.MAX_VALUE); 
        
        dp[0] = 0; 
        for(int i = 0; i < nums.length; i++){
            for(int j = i; j <= i + nums[i] && j < nums.length; j++){
                dp[j] = Math.min(dp[j],dp[i] + 1); 
            }
        }
        
        return dp[nums.length-1]; 
    }
}

class Solution {
public:
    int jump(vector<int>& nums) {
        vector<int> dp(nums.size(),INT_MAX); 
        dp[0] = 0; 
        for(int i = 0; i < nums.size(); i++){
            for(int j = i; j <= i + nums[i] && j < nums.size(); j++){
                dp[j] = min(dp[j],dp[i] + 1); 
            }
        }
        return dp[nums.size()-1]; 
    }
};